5. ЭДС наводимое от движения намагниченного ротора.
Четвёртым слагаемым можно пренебречь, поскольку в большинстве ШД взаимоиндукция составляет лишь 10% от индуктивности обмоток. Также пренебрегаем последним слагаемым, поскольку его влияние заметно лишь на высоких частотах (если быть точным – частоты за среднечастотным резонансом – для выбранного двигателя около 10 об. в сек). После данных упрощений перепишем уравнения для токов в обмотках статора.
|
|
|
|
(13)
(14)
Таким образом, мы получили 3 уравнения: (10), (13) и (14), которые полностью описывают ШД с приемлемой точностью. Здесь на вход подаём 2 напряжения, на выходе получаем угол поворота ротора.
2.4 Математическая модель ШД в MATLAB.
Для моделирования всех процессов в дипломном проекте используем MATLAB версии 7.5.0.342 (R2007b) с Simulink версии 7.0 , 2007-го года выпуска. В этом пакете уже есть модель шагового двигателя (если раскрыть дерево элементов: библиотека SimPowerSystems -> Machines), но у этой модели нельзя в полной мере настроить параметры шагового двигателя, поэтому создадим собственную модель ШД. Для этого в прошлой главе были выведены все необходимые формулы. Имена блоков на английском, поскольку использование кириллических букв в этом случае невозможно (из-за невозможности сохранения и открытия файла).
Итак, начнём с уравнения движения ротора, формула (10). Таким образом можно представить это уравнение в среде Simulink, рис 2.4.1:
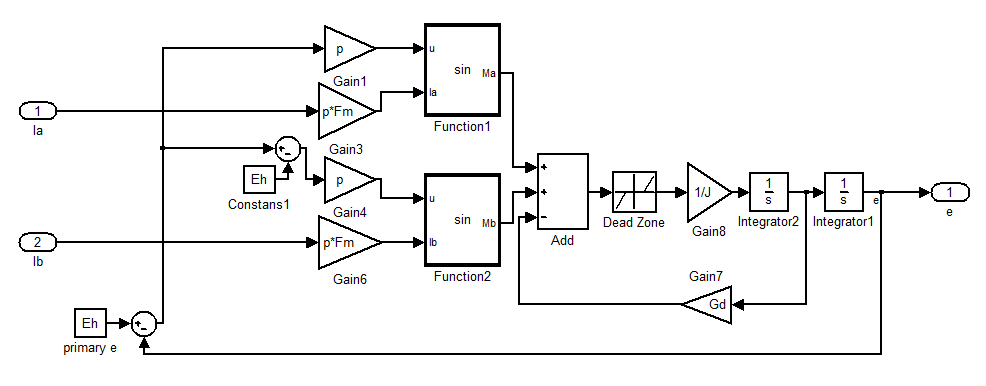
Рис. 2.4.1
Приведём ещё раз уравнение (10) для удобства просмотра:
 (10)
(10)
На вход системы подаётся 2 источника тока, которые в реальности подаются на катушки ШД. А на выходе получаем угол поворота ротора. В самом общем случае сигналы Ia и Ib могут быть любыми, но для вращения двигателя эти сигналы должны быть синусоидальные и сдвинутые по фазе на 90 градусов, при этом на выходе получим угол поворота, выращенный в радианах, который будет линейно возрастать.
Рассмотрим структуру модели. Элементы Gain1, Gain3, Gain4, Gain6, Constans1=Hh образуют коэффициенты синусов (образно говоря - обвес), 2-х последних слагаемых уравнения. Function1,2 являются обычными функциями синуса с коэффициентом. На выходе из каждой из этих функций получаем составляющую момента от соостветствующей обмотки ШД. Эти моменты алгебраически суммируются, кроме того из их суммы вычитается динамическая сила трения (местная обратная связь в этой системе). Далее идёт блок Dead Zone – мёртвая зона, которая учитывает статическое трение, характеризуется коэффициентом Gs. Теперь мы получили мгновенное значение момента, с учётом всех сил трения. Далее момент делится на общий момент инерции (Gain8), получая угловое ускорение с размерностью [рад/сек^2]. Далее блок Integrator1 преобразует этот сигнал в угловую скорость [рад/сек]. Сигнал угловой скорости в свою очередь также поступает на интегратор Integrator2, на выходе которого получаем угол e . Далее угол [рад] поступает на вход системы, как главная отрицательная связь, поступает на вход системы и входит в состав функций синусов. Блок primary e вводит первоначальную ошибку в систему.
Приведём часть кода m-файла, для данной модели (Рис. 2.4.1) (полностью m-файл вы можете посмотреть в файле steping_motors_v8.ru):
p=50; %редукция
S=200; %кол-во шагов на оборот
Fm=6.36e-3; %токосцепление магнита [Тл*м^2]
Jr=13.5e-6; %момент инерции ротора [кг*м^2]
Eh=pi/100; %величина шага [рад]
Gst=0.075; %статический момент трения [Н*м]
Gd=0.0027; %демпфирующий момент трения [Н*м*с/рад]
Mx=2.0; %масса суппорта X [кг]
Dc=15e-3; %радиус зубчатого колеса [м]
J=Jr+Mx*Dc*Dc/4 %общий момент инерции [кг*м^2]
В m-файле упущены некоторые расчёты. Поэтому рассмотрим их отдельно здесь.
Расчёт токосцеления магнита. Используем уравнение движения ротора (10). Известен момент удержания из паспортных данных а также номинальный ток обмоток. Важно также учесть что этот момент измерялся при 2-х запитанных обмотках. Примем то, что ротор находится в покое, тогда все члены, кроме слагаемых с синусами можно отбросить. И вывести из полученной формулы Fm:
|
|
|
|
(15)
(16)
Помним, что момент удержания – это максимальный момент, при ошибке равной шагу, понятно что при этом оба синуса станут равные корню из 2-х на 2. После этих упрощений получаем формулу:
|
|
(17)
Подставив значения Mnom=1.26 м*Н и Inom=2.8А, получим ответ указанный в m-файле.
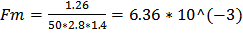 [Тл*м^2] токосцеление магнита
[Тл*м^2] токосцеление магнита
Измерение коэффициентов Gd и Gs. Теоретический расчёт этих величин потребовал бы моделирования весьма сложных физических процессов, поэтому я измерил их практическим путём. Для этого понадобился динамометер, секундомер и практически реализованная ось X, с суппортом и двигателем. Сначала измерение силы трения проводилось при малых скоростях движения: сила составила в этом случае 10Н, откуда можно сразу вывести Gs (момент статического трения):
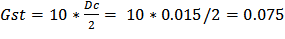 [м*Н] статическое трение
[м*Н] статическое трение
Далее измерим силу трения при значительной скорости. Сила составит 15 Н. При этом также сделаем замер расстояния и времени равномерного движения суппорта во время измерений. Получили: время 3 сек. и расстояние 210мм. Скорость движения составит:
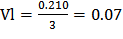 [м/с] линейная скорость
[м/с] линейная скорость
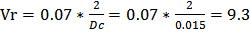 [рад/с] угловая скорость
[рад/с] угловая скорость
Далее чтобы получить динамический момент трения, вычтем из общего момента от 15 Н момент статического трения и поделим на угловую скорость:
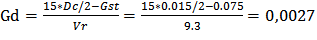 [м*Н*с/рад]
[м*Н*с/рад]
момент динамического трения
Замена источников тока на источники напряжения.
Обмотки ШД обладают собственной индуктивностью, поэтому в них ток не может резко возрасти, что накладывает дополнительное условие, если мы используем источники напряжений в модели. См. формулы (13) и (14) выведенные ранее:
|
|
|
|
(13)
(14)
Каждую из этих формул в конечном итоге можно представить в виде передаточных функций.
В этих формулах R = r+Rd, где r – собственное сопротивление обмотки, Rd – добавочное сопротивление, которое мы сами подключаем последовательно в цепи обмотки для будущих экспериментов, по умолчанию его будем считать равным 0.2 Ом – сопротивление ключей.
Итак приведём формулу (13) к доступной форме для добавления к математической модели в Simulink. Сделаем замену операторного аналога:
|
|
(18)
Тогда:
|
|
|
|
|
|
(19)
Понятно что для катушки В передаточная функция будет аналогичная. Эта функция преобразует напряжение в ток обмотки. Теперь добавим её к математической модели ШД:
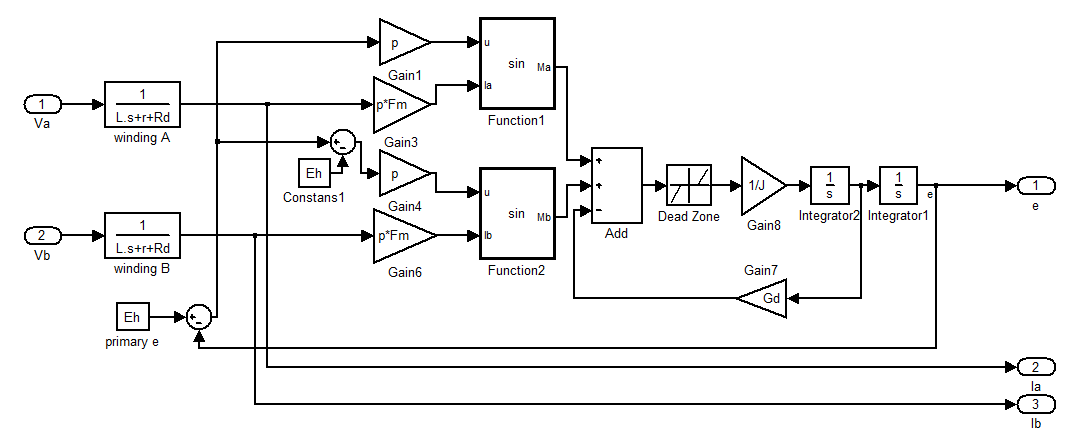
Рис. 2.4.2
Теперь мы имеем полноценную модель ШД. На вход подаются напряжения, а на выходе имеем угол положения ротора в [рад]. Кроме того для дополнительного анализа системы выносятся текущие значения токов Ia и Ib для построение графика зависимости этих величин от времени. Блоки Winding A,B преобразуют сигналы напряжений в сигналы токов. Объединим эту модель в субсистему для удобства дальнейшего использования:
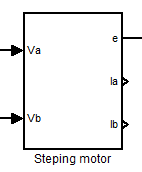
Рис. 2.4.2
Приведём параметры обмоток, записанные в m-файле:
L=2.5e-3 %индуктивность обмотки статора [Гн]
r=0.9 %сопротивление обмотки статора [Ом]
Rd=0.2; %дополнительное сопротивление [Ом]
2.5 Математическая модель драйвера и микроконтроллера в MATLAB.
Начнём с составления математической модели драйвера. Для этого нужно выбрать подходящий драйвер для данного двигателя.
Требуется менять полярность на обмотках двигателя, и управлять током посредством ШИМ. Для это необходим Н-мост и логика управления. Как вариант можно использовать отдельные силовые ключи и драйвера для их управления. Но схема получится очень сложной, появится множество ошибок при пайке. Поэтому я остановился на интеллектуальном мосте IR3220 компании International Rectifier. Также я рассматривал ещё несколько вариантов такого рода микросхем, но этот драйвер опережает их по всем параметрам. Следует заметить, что данный драйвер предназначен для управления двигателем постоянного тока, но 2 таких драйвера вполне способный полноценно управлять шаговым двигателем (то есть 2-мя обмотками), для этого следует написать соответствующую программу на микроконтроллере.
Для работы моста используется микросхема IR3220 (с 2-мя ключами верхнего уровня и логикой управления) и 2 транзистора-компаньона (транзисторы нижнего уровня) IRF7474.
Основные параметры из документации:
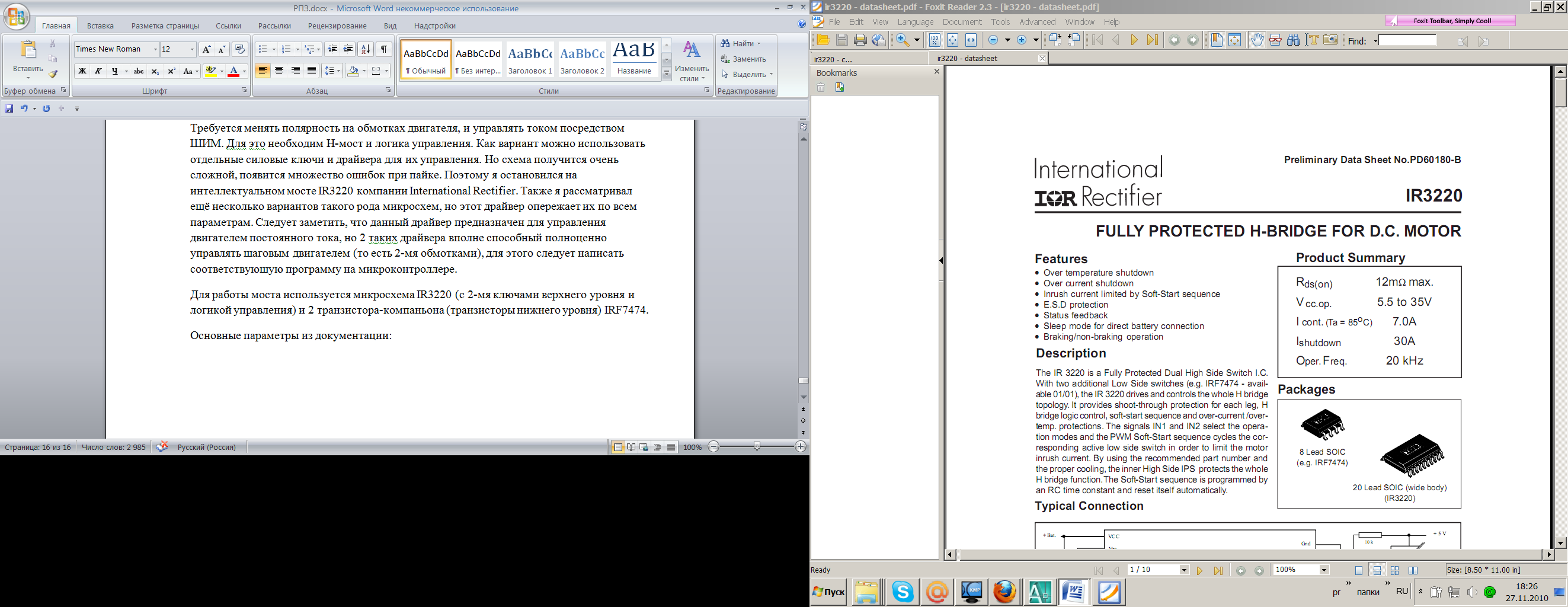
(рис 2.5.1)
Рассмотрим подробнее архитектуру драйвера:
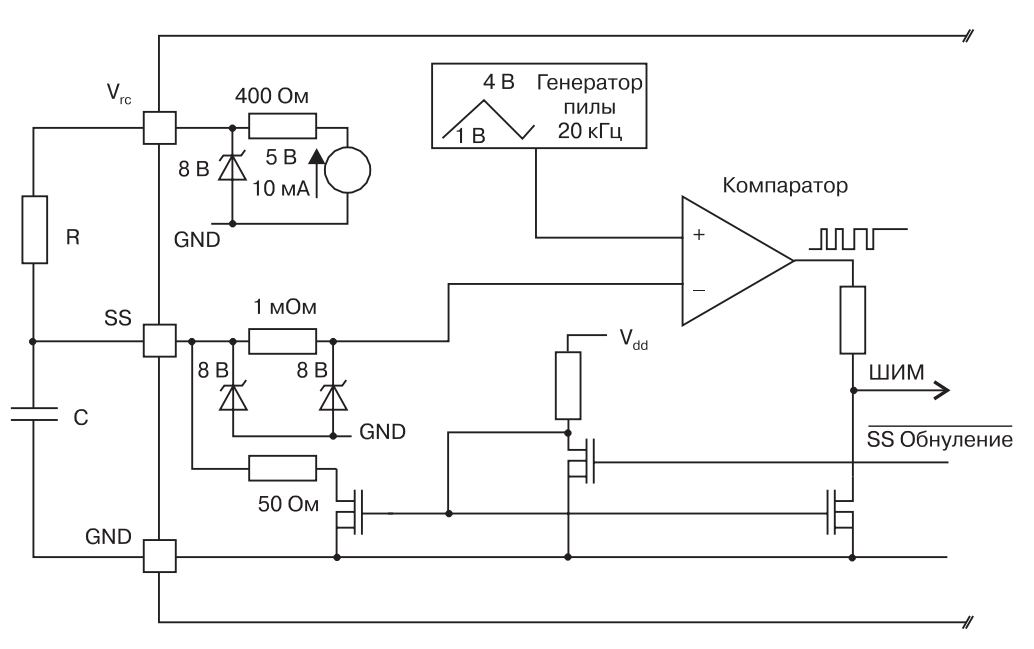
(рис 2.5.2)
На рис 2.5.2 изображена та часть логической схемы драйвера, которая формирует ШИМ из входного аналогового сигнала, который в свою очередь поступает от микроконтроллера. Здесь вместо него изображён конденсатор, который используется в режиме плавного возрастания уровня ШИМ-а. В состав микросхемы входит блок, формирующий ШИМ-сигнал. Он состоит из генератора напряжения пилообразной формы с частотой около 20 кГц и компаратора напряжения. Пилообразный сигнал сравнивается с напряжением на выводе SS, в результате чего формируется ШИМ-сигнал, который поступает на ключи нижнего уровня. Пилообразный сигнал изменяется в пределах 1...4 В, а коэффициент заполнения1 ШИМ-сигнала (K3) — пропорционально напряжению Vss, от 0 (Vss < 1 В) до 100% (Vss > 4 В). Но для упрощения модели мы будем использовать уровни 0..5 В.
Разумеется, контроллер не может дать аналоговый сигнал. Только цифровой в качестве своего ШИМ-сигнала (в частности со своей частотой). И мы не будем использовать фильтр, чтобы его сгладить перед подачей в драйвер. В конце концов формирователь ШИМа внутри драйвера нам не потребуется вовсе. Потребуется только небольшая его конструктивная часть – компаратор. Который будет всего лишь сравнивать сигнал МК со своим пилообразным сигналом. Вот почему для нас совершенно не имеет значения какой этот сигнал – пилообразный или просто постоянный во времени. И здесь может возникнуть противоречие, которое ставит пред нами вопрос: где находиться формирователь ШИМ-а? Ответ на него различный для различных пониманий вопроса. В реальности формирователь ШИМ-а находиться в МК, а в виртуальной модели, которую мы здесь проектируем находиться в драйвере. Это сделано для более наглядного представления сигналов, которые передаются от устройства к устройству. МК кроме ШИМ-а передаёт ещё логические сигналы N1 и N2, по ним драйвер изменяет направление напряжения питания для ШД. См. рис. 2.5.3, где изображена общая структура драйвера:
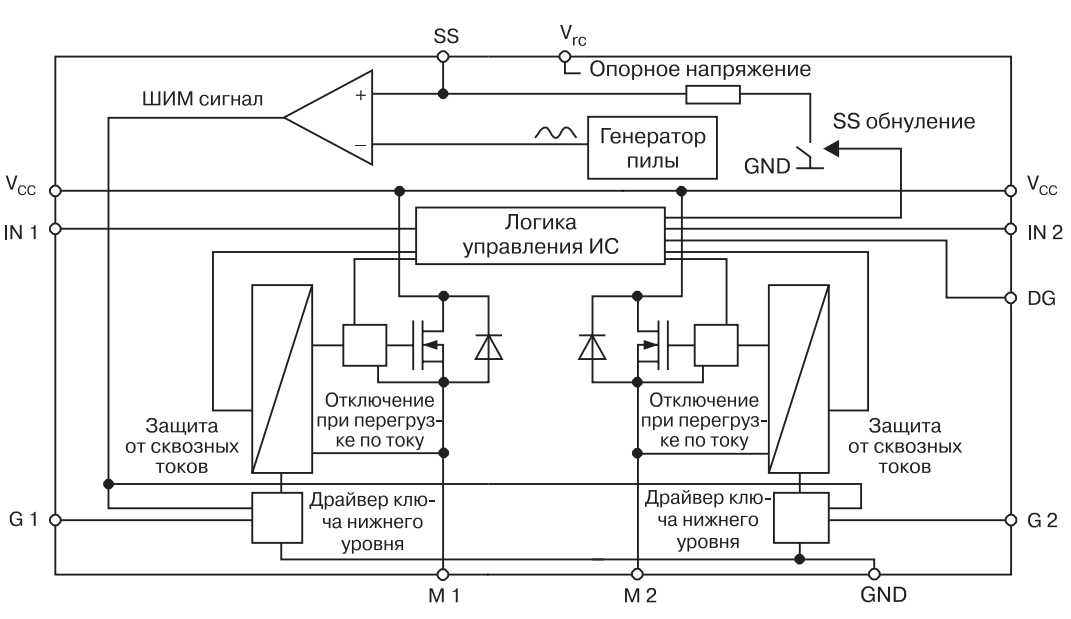
(рис 2.5.3)
В нашей математической модели МК будет посылать аналоговый сигнал драйверу. Его величина будет определять уровень ШИМ-а. А если МК подаст отрицательный сигнал – в этом случае драйвер инвертирует напряжение питания для ШД. И тогда отпадает необходимость вводить дополнительные логические сигналы: IN1 и IN2. Теперь, согласовав все нюансы и допущения мы можем составить следующую модель драйвера в MATLAB, рис 2.5.4:
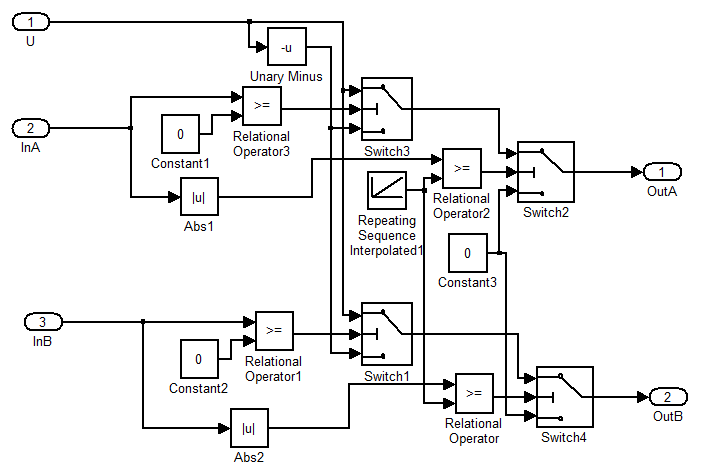
(рис 2.5.4)
Здесь на вход подаётся напряжение питания и 2 управляющие входа, для каждой обмотки. Выходами являются силовые выводы: напряжения подаваемые на входы шагового двигателя. Параметры из m-файла для этой модели:
Tvt=0.000001 %время переключения транзисторов [с]
Tpwm=0.00005 %период шима [c]
U=24 %напряжение питания ШД [в]
Центральный блоком модели является источник пилообразного сигнала Repeating Sequence Interpolated1, и на его выходе получаем:
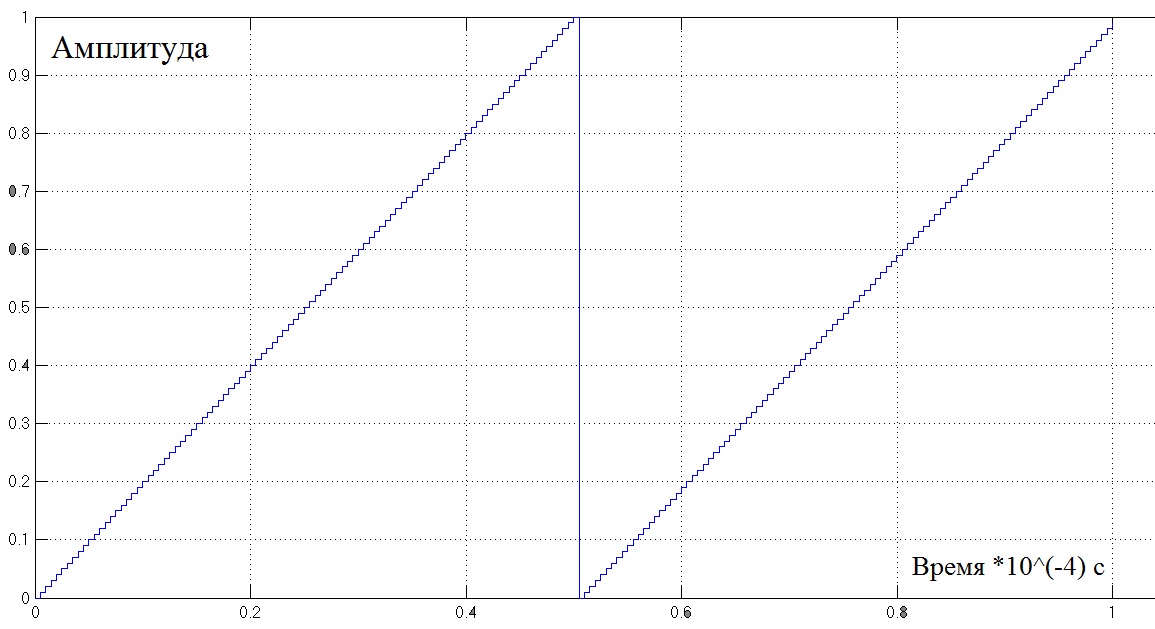
(рис 2.5.5)
В данном пилообразном сигнале амплитуда возрастает дискретно по 0.01 от своего максимального значения. Точность установки ШИМ-а в 2 значащих знака вполне нас устраивает, а дальнейшее уменьшение этой дискреты сильно увеличит время моделирования сигнала.
Теперь рассмотрим сигналы на выходе и на входе драйвера:
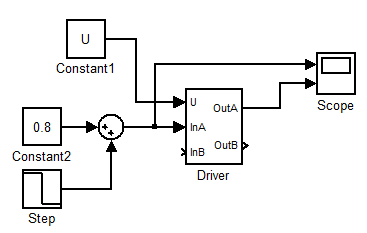
(рис 2.5.6)
На рис 2.5.6 изображена схема для тестирования драйвера. А ниже результат тестирования:
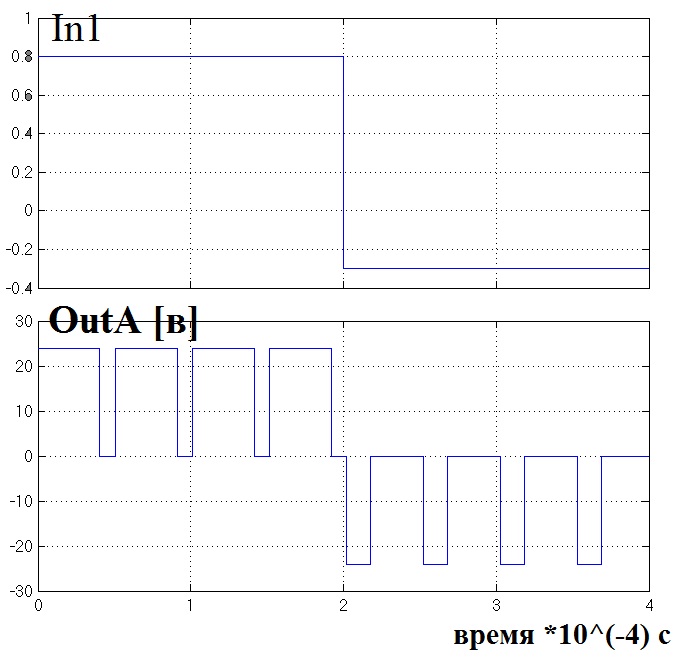
(рис 2.5.6)
На вход подаётся сигнал с микроконтроллера. Следует заметить что максимальная его величина не 5 вольт, а безразмерная единица. Условно она показывает какой скважности должен быть ШИМ-сигнал. Сначала входной сигнал положителен, затем отрицательный, ШИМ меняется соответствующим образом. Это реализуется с помощью нескольких переключателей: Switch1-4.
Математическая модель микроконтроллера.
Среди множества библиотек MATLAB нет готовых моделей таких электронных устройств как микроконтроллеры. Хотя имеются в наличии резисторы, транзисторы и другие электронные элементы, из которых можно составить электронные схемы. Ответ на вопрос: существуют ли полноценные симуляторы МК в составе электронных схем, конечно есть. Например такой мощный пакет как Proteus способен моделировать микропроцессоры и МК самых различных архитектур, кроме того в нем есть огромная библиотека электронных компонентов, которую удобно использовать даже как просто справочник. Но в этой программе нет возможности в полной мере провести анализ системы, так как это нам позволяет сделать MATLAB. С другой стороны нам не обязательно моделировать абсолютно все элементы микроконтроллера вместе со всеми его регистрами. В простейшем случае нам требуется получить желаемый сигнал, т. е. тот угол поворота ротора. И затем просто сравнить желаемый и полученный сигнал и выявить ошибку. Если она будет в пределах допуска, то можно приступать к реализации системы: писать программу на МК и разрабатывать схему управления.
Начнём с желаемого результата:
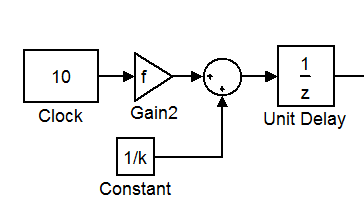
(рис 2.5.6)
На данном этапе моделирования используются следующие параметры:
k=2; %деление шага
f=100; %частота шаг в сек
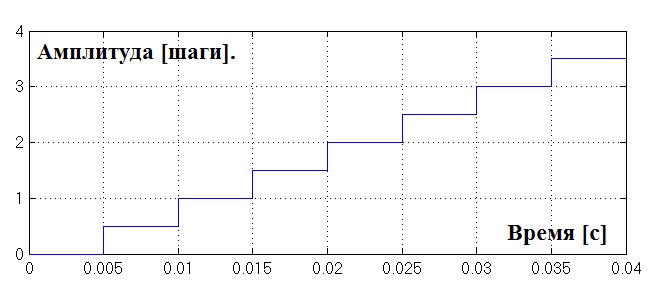
В модели на рис 2.5.6 используется блок времени Clock, который выводит текущее время в секундах. Далее после некоторого приведения сигнал обрабатывает бок Unit Delay, который из линейно-возрастающего сигнала получает ступенчатый, с частотой дискредитации 1/(f*k):
(рис 2.5.7)
Как видно из рас 2.5.7 на выходе получаем требуемый угол ротора как зависимость от времени. Ротор должен поворачиваться каждые 0.01 секунды на один шаг против часовой стрелки, делая при этом полушаги каждые 0.005 сек. (такты). В m-файле задаём необходимую комбинацию k и f (частоты и деления шага), и получаем требуемый сигнал.
Кроме этого микроконтроллер должен сформировать сигналы для драйвера. Причём этих сигналов должно быть два, они изменяются по законам sin и cos. Для этого добавим к системе на рисунке (рис 2.5.6) блоки указанные функции получив в результате следующую систему:
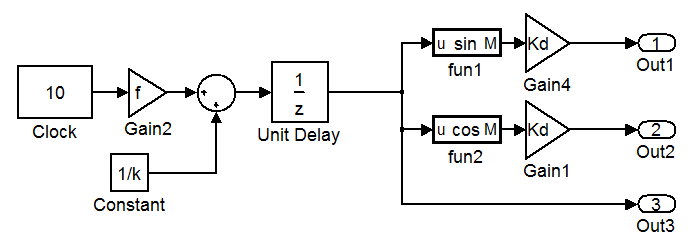
(рис 2.5.8)
Здесь кроме всего выше сказанного появляется коэффициент Kd, который меньше единицы. Он нужен для того чтобы снизить общий уровень ШИМ, таким образом чтобы максимальный ток в обмотке был равен номинальному. Источник питания 24 вольта, а сопротивления обмотки не доходит и до 1 Ома. Значит при ШИМ=100% ток очень быстро достигнет десятков ампер, что недопустимо. Коэффициент Kd рассчитывается по закону ома, смотрите лист m-файла:
Inom=2.8 %номинальный ток [А]
Kd=Inom*(Rd+r)/U %коэфф усиления драйвера
(20)
Далее проведём тест системы для прежних значений частоты и деления шага:
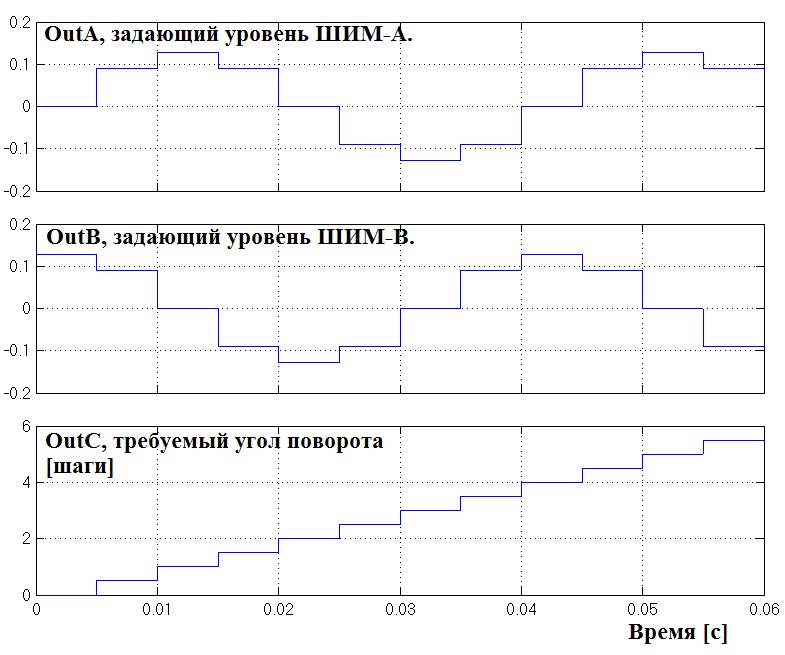
(рис 2.5.8)
Из графика видно, что коэффициент Kd примерно равен 1.2 . А управляющие сигналы для формирования ШИМ, полностью соответствуют тем теоретическим выкладкам, которые были сделаны в главе “Фундаментальные уравнения”, см. рис 2.3.3. Модель удобна тем, что коэффициент деления шага k можно задать любое, при этом частота вращения ротора останется неизменной.
2.6 Резонанс ШД и борьба с ним.
Шаговым двигателям свойственен нежелательный эффект, называемый резонансом. Эффект проявляется в виде внезапного падения момента на некоторых скоростях. Это может привести к пропуску шагов и потере синхронности. Эффект проявляется в том случае, если частота шагов совпадает с собственной резонансной частотой ротора двигателя. Когда двигатель совершает шаг, ротор не сразу устанавливается в новую позицию, а совершает затухающие колебания. Дело в том, что систему ротор – магнитное поле – статор можно рассматривать как пружинный маятник, частота колебаний которого зависит от момента инерции ротора (плюс нагрузки) и величины магнитного поля. Это значит что резонансная частота зависит от тока, поданного на обмотки. Поэтому для нахождения этой частоты будем использовать номинальный ток.
Итак определим частоты, на которых ШД ведёт себя неустойчиво. Для этого используем ранее полученную модель ШД (Steping motor) и подадим на одну из его обмоток постоянный номинальный ток, а на другую синусоидальный источник тока с плавно меняющейся частотой и амплитудой равной также номинальному току.
Прогонять сигнал через драйвер нецелесообразно, поскольку потребуется очень много времени на вычисления. К примеру: 0.01 секунда симуляции всей модели требует 10 секунд машинного времени (процессор Intel Core 2 Duo P750). А для прохождения частотного диапазона потребует 20 секунд симуляции модели и в 1000 раз больше машинного времени. Это 5 часов работы компьютера. Поэтому модель драйвера не используем. Но напряжение следует оставить прежним 24 вольта. Для стабилизации тока используем добавочное сопротивление. Нужно увеличить его сопротивление до такого уровня, чтобы ток не поднимался выше номинального:
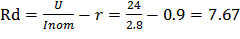 [Ом] добавочное сопротивление
[Ом] добавочное сопротивление
(21)
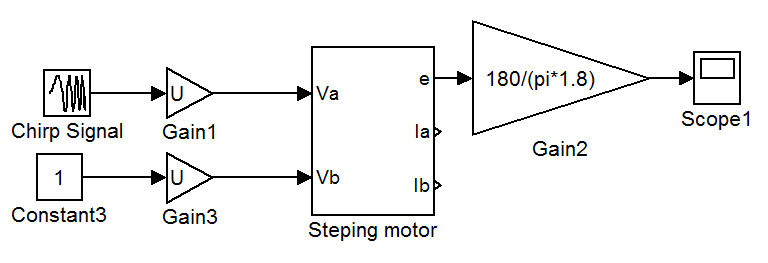
Рис 2.6.1
Блок с названием Chirp Signal, он подаёт сигнал с амплитудой равной 1 и частотой, которая линейно увеличивается с 0 до 200 Гц в течение 20 сек. Блок Gain2 переводит размерность [рад] в шаги, где каждый шаг равен 1.8 градуса (смотрите паспорт ШД). Запустим симуляцию:
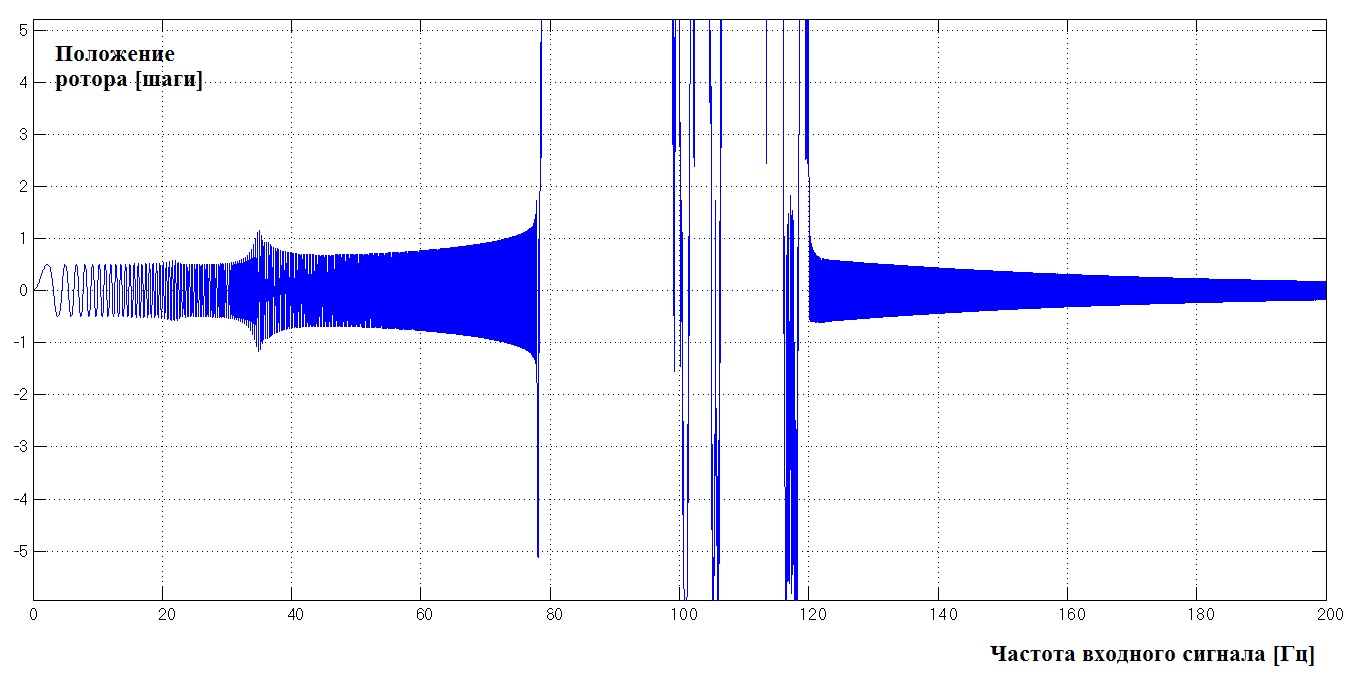
Рис 2.6.2
Этот график как никак лучше отображает каким образом резонанс может повлиять на устойчивость двигателя. На низких частотах всё происходит так как задумано (частоты до 15 Гц) двигатель колеблется от 0.5 шага до -0.5 не выходя за рамки этих частот. Смотрите рисунок рис 2.3.3 чтобы свериться с теорией. Далее скорость ротора увеличивается и инерция системы даёт о себе знать: ротор словно раскачивается, выходит за пределы дозволенной амплитуды. Затем амплитуда несколько снижается (частоты около 40 Гц), из-за силы трения. Но дальше и она не может воспрепятствовать увеличению амплитуды. Как только амплитуда превышает 1.5 шага, сила, возвращяющая ротор к нулевому положению начинает действовать в противоположном направлении и ротор продолжает вращаться, превышая 1 оборот. Далее он ведёт себя непредсказуемо. Здесь нет отдельно взятой резонансной частоты, здесь целая область частот с неустойчивой работой двигателя, а именно частоты от 58 до 120 Гц. Как только мы выходим за область неустойчивости, ротор может оказаться где угодно – нередко на 20-40 шагов от начального положения. На рис. 2.5.8 выбран вариант когда ротор вернулся в нулевое положение – это большое везение.
Итак, какой способ следует выбрать для борьбы с резонансом. Способы:
1. применение эластичных материалов при выполнении механических муфт связи с нагрузкой. Эластичный материал способствует поглощению энергии в резонансной системе, что приводит к затуханию паразитных колебаний.
2. применение вязкого трения. Выпускаются специальные демпферы, где внутри полого цилиндра, заполненного вязкой кремнийорганической смазкой, может вращаться металлический диск. При вращении этой системы с ускорением диск испытывает вязкое трение, что эффективно демпфирует систему.
3. электрические методы борьбы с резонансом. Колеблющийся ротор приводит к возникновению в обмотках статора ЭДС. Если закоротить обмотки, которые на данном шаге не используются, это приведет к демпфированию резонанса.
4. существуют методы борьбы с резонансом на уровне алгоритма работы драйвера. Например, можно использовать тот факт, что при работе с двумя включенными фазами резонансная частота примерно на 20% выше, чем с одной включенной фазой. Если резонансная частота точно известна, то ее можно проходить, меняя режим работы.
5. при старте и остановке нужно использовать частоты выше резонансной. Увеличение момента инерции системы ротор-нагрузка уменьшает резонансную частоту.
6. самой эффективной мерой для борьбы с резонансом является применение микрошагового режима.
Все способы связанные с конструктивными доработками системы нам не подходят, поскольку это увеличит сложность системы, а следовательно её надёжность. Будем бороться с резонансом программными методами. Например использование микрошагового режима. Нам в любом случае придётся вводить этот режим, чтобы увеличить точность системы. Таким образом убьём 2-х зайцем одним ударом.
Когда используется не микрошаговый режим, основной причиной появления колебаний является прерывистое вращение ротора. При осуществлении шага ротору толчком сообщается некоторая энергия. Этот толчок возбуждает колебания. Энергия, которая сообщается ротору в полушаговом режиме, составляет около 30% от энергии полного шага. Поэтому в полушаговом режиме амплитуда колебаний существенно меньше. В микрошаговом режиме с шагом 1/32 основного при каждом микрошаге сообщается всего около 0.1% от энергии полного шага. Поэтому в микрошаговом режиме явление резонанса практически незаметно.
Сразу можно привести пример, подтверждающий эффективность использования резонанса, на нашей модели:
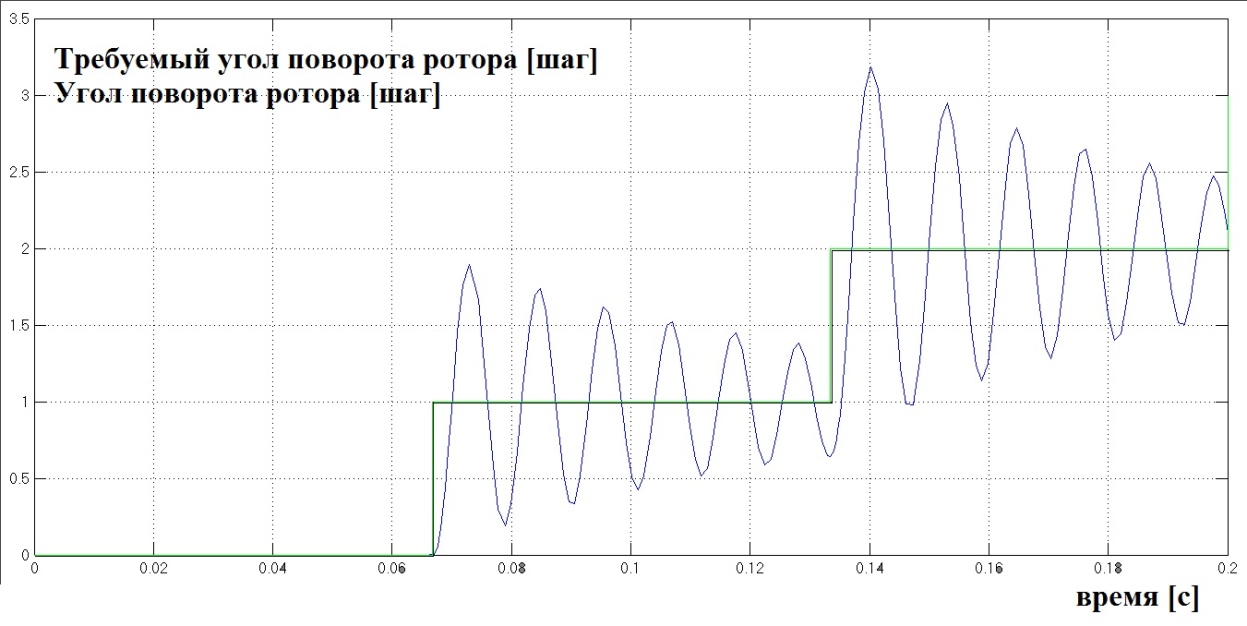
Рис 2.6.3 (полношаговый режим)
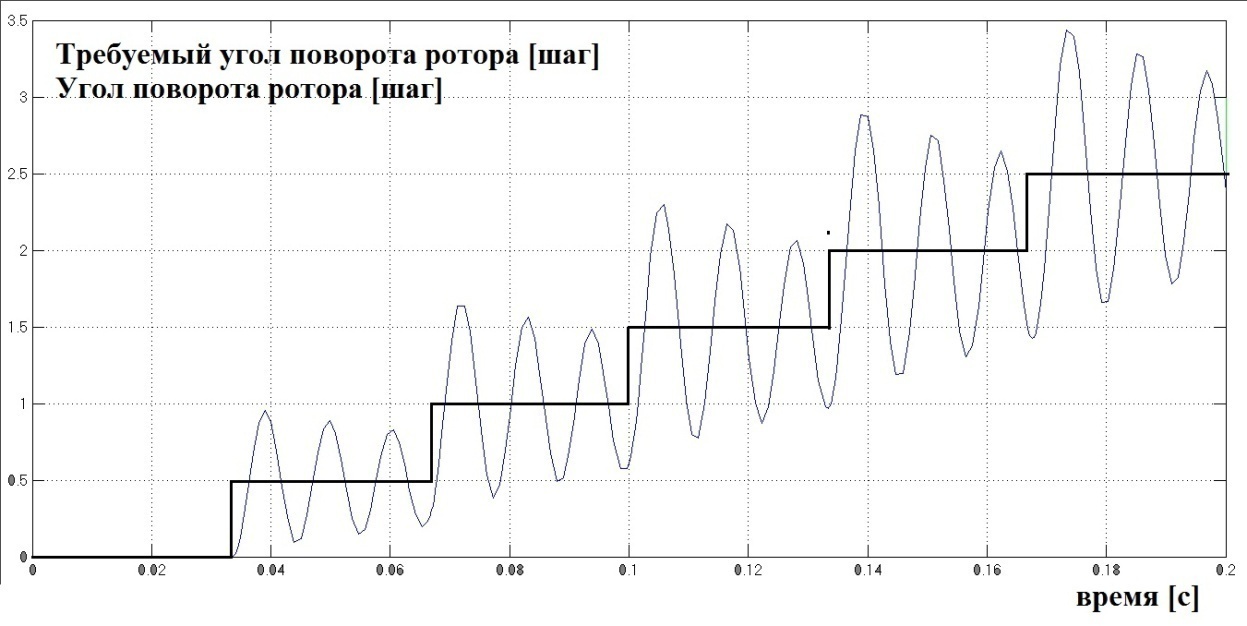
Рис 2.6.4 (деление шага на 2)
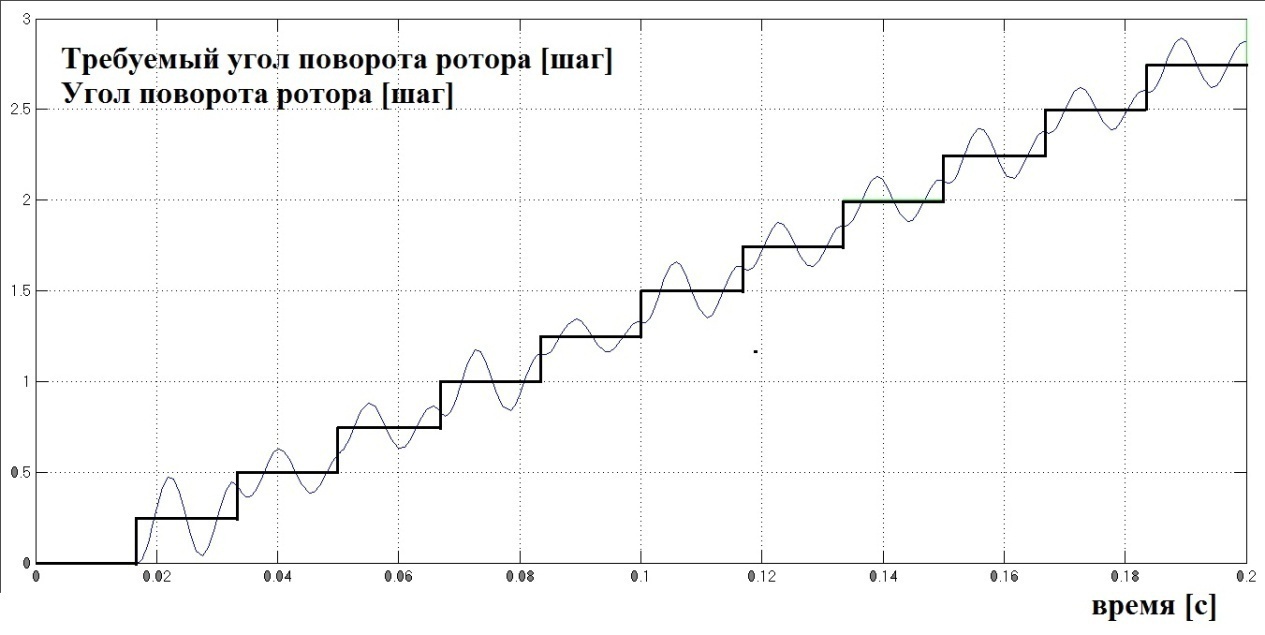
Рис 2.6.5 (деление шага на 4)
Здесь используются следующие настройки: частота f=15 Гц и деление шага k от 1 до 3. На рис 2.6.3-2.6.5 изображены графики требуемых углов поворота (задаётся микроконтроллером) и получаемых в результате углов поворота на выходе из модели ШД. Видно что ошибка довольно сильно уменьшается с каждым делением шага. Для получения этих графиков использовалась модель на рис 2.6.3 (сохранена в файле steping_motors_v8_1_1). Для анализа резонанса будем очень часто обращяться к этой заготовке. Модель отличается от модели на рис 2.6.1 добавлением микроконтроллера, осцилографа для измерения ошибки по углу (единица измерения шаг) с соответствующей цепью и добавлением к осцилографу для измерения угла мультиплексированной шины с требуемым угом от микроконтроллера (для удобного сравнения как на рис 2.6.3-рис 2.6.5).
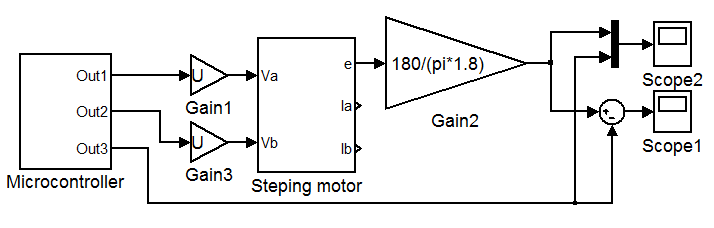
Рис 2.6.3
Для наиболее полного анализа резонанса проведём следующие измерения (с помощью модели, изображённой на рис 2.6.3). Требуется построить график зависимости частоты подаваемого сигнала с микроконтроллера от максимальной ошибки по углу положения ротора. Причём получить эту зависимость для каждого режима: полношагового, с делением шага на 2, с делением шага на 4, и если потребуется на 8. Следует заметить тот факт, что автоматизировать процесс нельзя, потому что в некоторых случаях из-за резонанса двигатель теряет устойчивость и пропускает шаги в некоторых случаях на сотни шагов. Кроме того в начале работы ШД стоит на месте, ему нужно набрать скорость, при этом ошибка также ведёт себя каждый раз по разному. Приходиться вручную задавать частоту, моделировать процесс (что занимает в среднем около 10 сек.) и смотреть ошибку на выходе системы, и так точку за точкой записывать в таблицу эксель (смотрите Таблицу 2.6.1). В графической форме эти данные представлены на листе А1, поскольку здесь не было бы видно деталей.
Таблица 2.6.1
| полношаговый режим | деление шага на 2 | деление шага на 4 | |||
| частота [Гц] | ошибка [шаг] | частота [Гц] | ошибка [шаг] | частота [Гц] | ошибка [шаг] |
| 1 | 0,900 | 1 | 0,500 | 1 | 0,250 |
| 2 | 0,900 | 2 | 0,500 | 2 | 0,300 |
| 5 | 0,900 | 5 | 0,410 | 5 | 0,250 |
| 10 | 1,100 | 10 | 0,440 | 7 | 0,170 |
| 15 | 1,150 | 15 | 0,950 | 8 | 0,500 |
| 16 | 1,100 | 17 | 0,450 | 9 | 0,170 |
| 17 | 0,650 | 20 | 0,330 | 10 | 0,160 |
| 20 | 0,900 | 25 | 0,590 | 11 | 0,230 |
| 25 | 1,000 | 30 | 0,280 | 15 | 0,145 |
| 30 | 1,300 | 35 | 0,310 | 20 | 0,195 |
| 35 | 1,000 | 38 | 0,350 | 21 | 0,280 |
| 37 | 0,510 | 39 | 0,380 | 22 | 0,930 |
| 38 | 0,550 | 40 | 2,000 | 23 | 0,800 |
| 39 | 2,000 | 41 | 1,200 | 24 | 0,660 |
| 44 | 2,000 | 45 | 1,000 | 25 | 0,530 |
| 45 | 2,000 | 50 | 0,770 | 26 | 0,420 |
| 46 | 2,000 | 55 | 0,540 | 30 | 0,215 |
| 47 | 2,000 | 60 | 0,400 | 40 | 0,135 |
| 48 | 1,100 | 70 | 0,300 | 50 | 0,135 |
| 49 | 0,950 | 80 | 0,270 | 75 | 0,148 |
| 50 | 0,900 | 90 | 0,260 | 100 | 0,159 |
| 51 | 0,850 | 100 | 0,270 | 120 | 0,167 |
| 52 | 0,750 | 120 | 0,280 | 150 | 0,180 |
| 55 | 0,720 | 150 | 0,300 | 200 | 0,198 |
| 60 | 0,720 | 180 | 0,310 | 250 | 0,217 |
| 65 | 0,550 | 200 | 0,320 | 300 | 0,235 |
| 66 | 0,520 | 250 | 0,340 | 400 | 0,273 |
| 67 | 2,000 | 300 | 0,360 | 500 | 0,310 |
| 68 | 2,000 | 400 | 0,400 | 700 | 0,381 |
| 69 | 2,000 | 500 | 0,435 | 737 | 0,394 |
| 70 | 2,000 | 700 | 0,505 | 738 | 2,000 |
| 75 | 2,000 | 726 | 0,515 | ||
| 80 | 2,000 | 727 | 2,000 | ||
| 90 | 2,000 | ||||
| 95 | 2,000 | ||||
| 98 | 2,000 | ||||
| 99 | 2,000 | ||||
| 100 | 2,000 | ||||
| 105 | 2,000 | ||||
| 110 | 2,000 | ||||
| 111 | 2,000 | ||||
| 112 | 2,000 | ||||
| 113 | 2,000 | ||||
| 114 | 2,000 | ||||
| 115 | 2,000 | ||||
| 116 | 1,400 | ||||
| 120 | 1,200 | ||||
| 130 | 0,630 | ||||
| 140 | 0,570 | ||||
| 150 | 0,550 | ||||
| 200 | 0,550 | ||||
| 250 | 0,560 | ||||
| 300 | 0,590 | ||||
| 400 | 0,640 | ||||
| 500 | 0,680 | ||||
| 600 | 0,720 | ||||
| 679 | 0,750 | ||||
| 680 | 2,000 | ||||
Конец таблицы 2.6.1
По части результатов. Обратите внимание, если ошибка превышает 2 шага, это значит, что потеряна устойчивость ШД, в этом случае обязательно будет пропуск шагов независимо от режимов работы.
Результаты измерений частотного анализа для различных режимов:
1. Полношаговый режим: потеря устойчивости на частотах 39-47 Гц и 67-115 Гц (2 области неустойчивасти). Самая высокая точность на частотах, после резонанса 0,55 шага. Максимальная частота вращения без плавного разгона 679 шагов в секунду.
2. Полушаговый режим: потеря устойчивости на частоте 40 Гц. Самая высокая точность на частотах, после резонанса 0,26 шага. Максимальная частота вращения без плавного разгона 727 шагов в секунду.
3. Полушаговый режим: потеря устойчивости отсутствует, есть пик с ошибкой 0,93шага на частоте 22 Гц. Самая высокая точность на частотах, после резонанса 0,14 шага. Максимальная частота вращения без плавного разгона 738 шагов в секунду.
Выводы (по резонансу в ШД):
При работе двигателя с номинальными токам наблюдается потеря устойчивости из-за резонанса на широкой полосе частот (39-47 Гц и 67-115 Гц). Для борьбы с резонансом был выбран метод: использование микрошагового режима, по следующим причинам:
1. Метод считается наиболее эффективным в решении проблемы резонанса в ШД.
2. При дроблении шага одновременно получаем более точное позиционирование ротора – что увеличивает точность системы.
3. Не требуется вносить каких-либо конструктивных изменений.
Анализ показал, что в ¼-шаговом режиме исчезает зона неустойчивости, влияние резонанса сильно уменьшилось, по сравнению с полношаговым режимом. Но наблюдается потеря точности на частоте 22-24 Гц, поэтому следует избегать подачу управляющего сигнала на ШД с этой частой.
Примечание: для ускорения вычислений к обмоткам был подключён добавочный резистор, чтобы стабилизировать ток в обмотках без использования ШИМ. Поэтому требуется дополнительно провести анализ динамики изменения тока в обмотках.
2.7 Форсирование тока в обмотках.
Индуктивность обмоток определяет время нарастания и спада тока. Поэтому если к обмотке приложено напряжение прямоугольной формы, форма тока не будет прямоугольной. При низких скоростях (рис. 16а) время нарастания и спада тока не способно сильно повлиять на момент, однако на высоких скоростях момент падает. Связано это с тем, что на высоких скоростях ток в обмотках двигателя не успевает достигнуть номинального значения (рис. 16б).
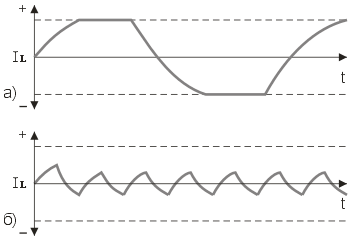
Рис. 2.7.1. Форма тока в обмотках двигателя на разных скоростях работы.
Для того, чтобы момент падал как можно меньше, необходимо обеспечить высокую скорость нарастания тока в обмотках двигателя, что достигается различными методами при использовании ШИМ:
1. Подключение добавочного сопротивления к обмоткам. При этом нужно увеличивать максимальный уровень ШИМа. При полном увеличении добавочного сопротивления до уровня ШИМ равным 100% источник напряжения практически превращается в источник тока и скорость изменения тока в обмотках значительно увеличивается, ценой падения КПД.
2. Программные методы. Эти методы предполагаю сохранение КПД, а вся корректировка управляющего сигнала находиться в микроконтроллере. Здесь возможны 2 подметода:
2.1 Проводиться синтез корректирующего устройства, которое в дискретной форме вноситься в микроконтроллер.
2.2 Импульсное форсирование. В начале каждого шага подаётся 100% - шим того или иного знака, иначе говоря импульс напряжения (в дальнейшем будем называть его форсирующий импульс), который приводит к быстрому изменению тока.
Следует рассмотреть все эти методы, чтобы выявить наилучший.
Для полноценного анализа создадим модель, которая будет иметь обмотку со всеми её параметрами, и логической схемой которая будет выводить время, когда ток достигнет уровня Inom с 5%-й погрешностью. Данную модель вы можете посмотреть в файле steping_motors_v8_p, сохраненный на диске:
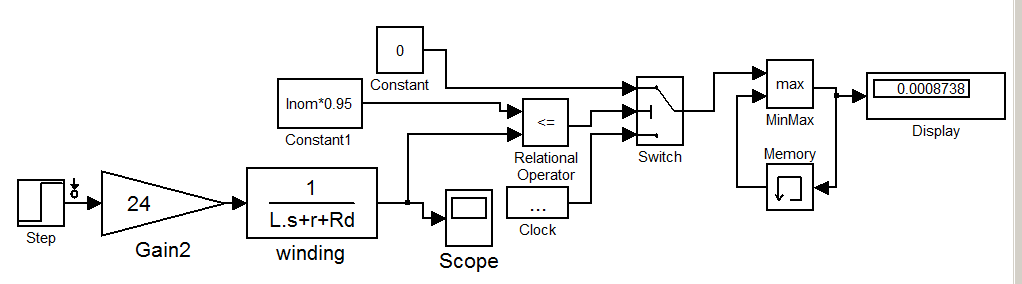
Рис. 2.7.2
Желаемый результат.
Какое время нарастания мы будем считать приемлемым. По проведённому ранее анализу было решено использовать режим микрошага с делением шага 1/4 . (Далее 1/4-шаговый режим). Требуемая скорость по техническому заданию 70 мм/сек. С запасом возьмём 75 мм/сек. Переведём в шаги за секунду (из расчёта того что один шаг соответствует 0.236мм): получаем 75/0.236 = 318 шагов в секунду. Следовательно частота изменений тока в процессе работы будет в 4 раза больше: 318*4 = 1272 импульсов в секунду. Период изменения тока 1/1272 = 786 мкс. Это минимальное время, за которое ток должен достичь требуемого уровня (с некоторой погрешностью разумеется), потому что в противном случае момент ШД начнёт сильно снижаться. На практике даже уложиться в это время недостаточно, нужно в несколько раз быстрее делать спад/нарастание тока. Поэтому формируется следующее требование к скорости измения тока: чем быстрее тем лучше, но не менее 780 мкс.
Время нарастания без коррекции.
На вход обмотки подаём ШИМ с такой скважностью (Kd), чтобы получить установившееся значение тока 2.8 ампер:
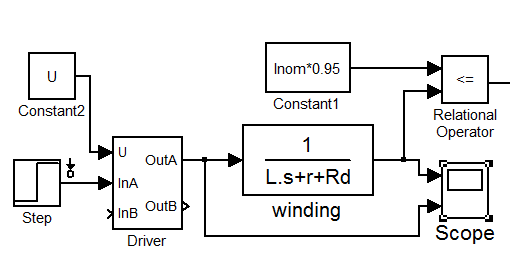
Рис. 2.7.3
В результате получаем время возрастания тока 7121 мкс. Что крайне неудовлетворительно, применительно к тем требованиям, которые были сформулированы ранее.
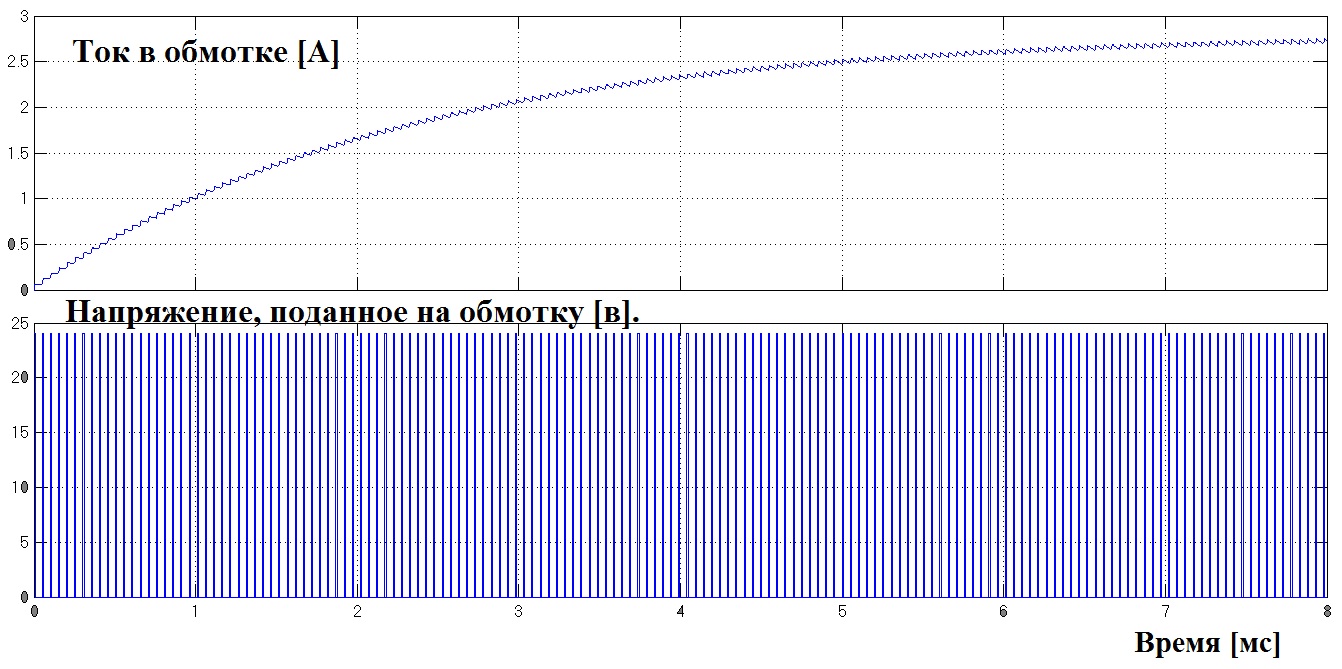
Рис. 2.7.4.
Необходима коррекция, для увеличения скорости изменения тока в обмотке.
Использование добавочного сопротивления.
Посмотрим, каких результатов можно добиться подключив добавочное сопротивление. Возьмём крайний случай, использовав максимальное значение сопротивления для номинального тока. Оно вычисляется по формуле (21) и было получено во время исследования резонанса (7.67 Ом). Кроме того само это исследование базировалось на этом методе форсирования токов добавочным сопротивлением.
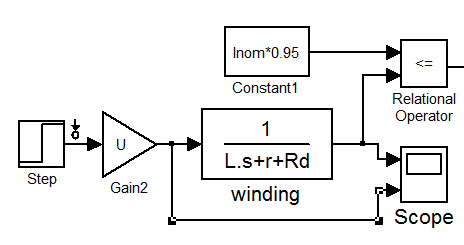
Рис. 2.7.5.
Схема заметно упростилась, потому что уровень ШИМа равен 100%, и поэтому драйвер не нужен вовсе. Время нарастания составляет теперь 870 мкс, что на порядок больше прошлого результата, но не подходит по требованиям к системе. На графике масштабирование шкалы времени осталось прежним, чтобы можно было сравнить с Рис. 2.7.4.
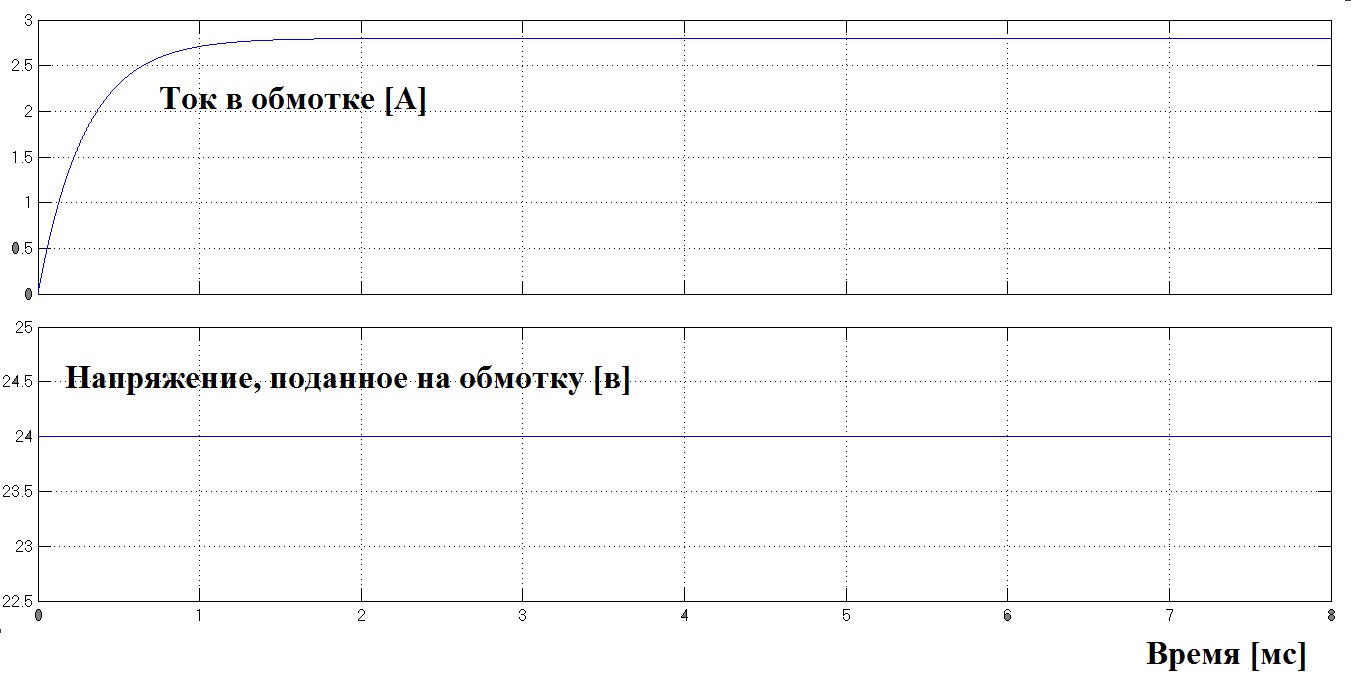
Рис. 2.7.6.
Следует заметить, что метод весьма неэкономичен. Поскольку на каждом двигателе находиться по 2 резистора с сопротивлением 7,67 Ома. И по каждому течёт ток 2.8 ампера. Следовательно тепловые потери на резисторах огромны: 2*7,67*2.8*2.8 = 120 Вт. Это сравнимо с мощным паяльником или среднестатистическим феном для волос. Причём данная мощность выделяется при питании одного двигателя, который сам потребляет около 60 Вт.
Корректирующие устройство в форме передаточной функции.
Требуется провести синтез системы, с целью добиться быстродействия. В начале построим ЛАЧХ неизменяемой части, то есть обмотки. У неё передаточная функция:
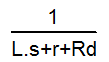
Для построения ЛАЧХ делаем входы и выходы из передаточной функции:
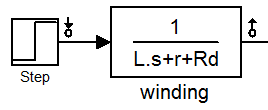
Далее заходим в меню Tools -> Control Design -> Linear Analysis… и производим линеаризацию модели:
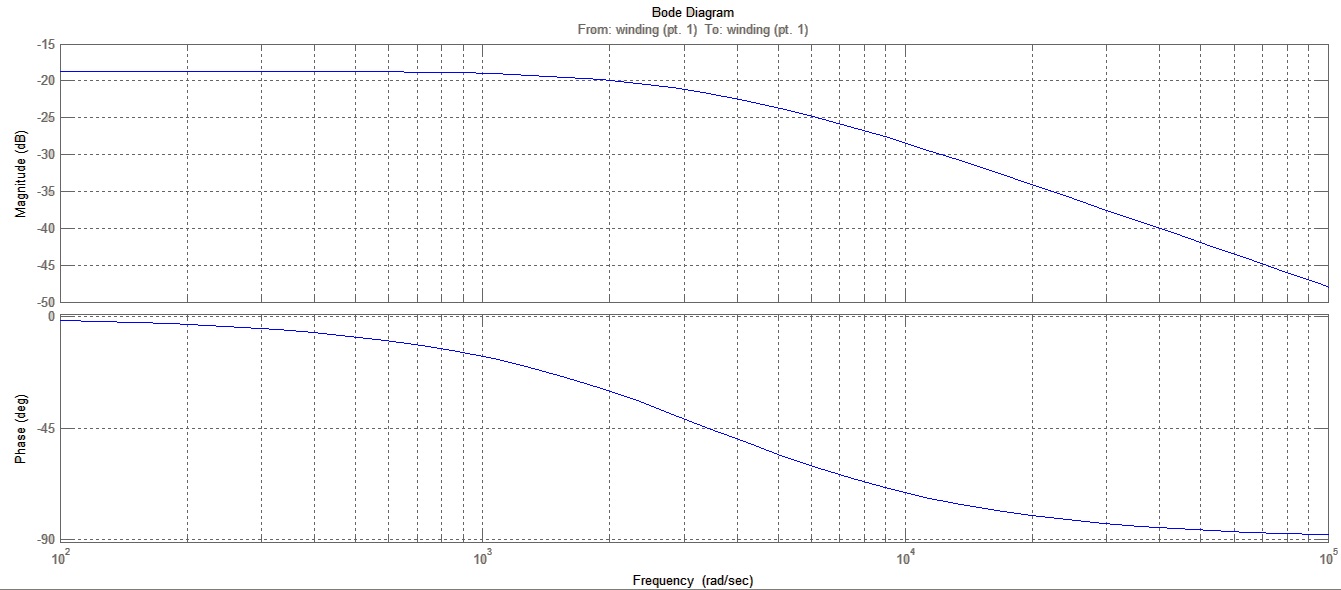
Рис. 2.7.7.
Здесь нужно поднять амплитуду на средних частотах, когда отставание по фазе составляет 45 градусов. Для этого была подобрана следующая передаточная функция корректирующего устройства:
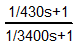
Руководствуясь данными из Рис 2.7.7 взяты приближённые коэффициенты, а затем, методом подбора они были уточнены.
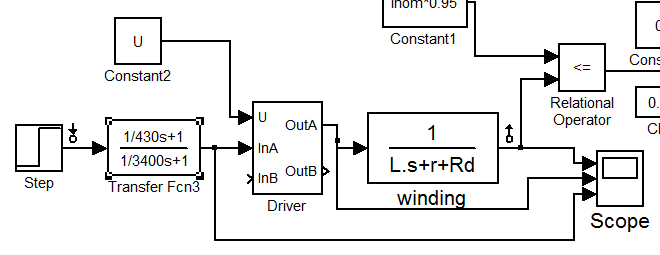
Рис. 2.7.7.
Здесь время возрастания тока почти такое же как при использовании добавочного сопротивления 810 мкс. Чего по прежнему недостаточно. Далее приведены временные графики возрастания тока, и управляющие сигналы, что даёт наглядное представление того, как работает корректирующие устройство:
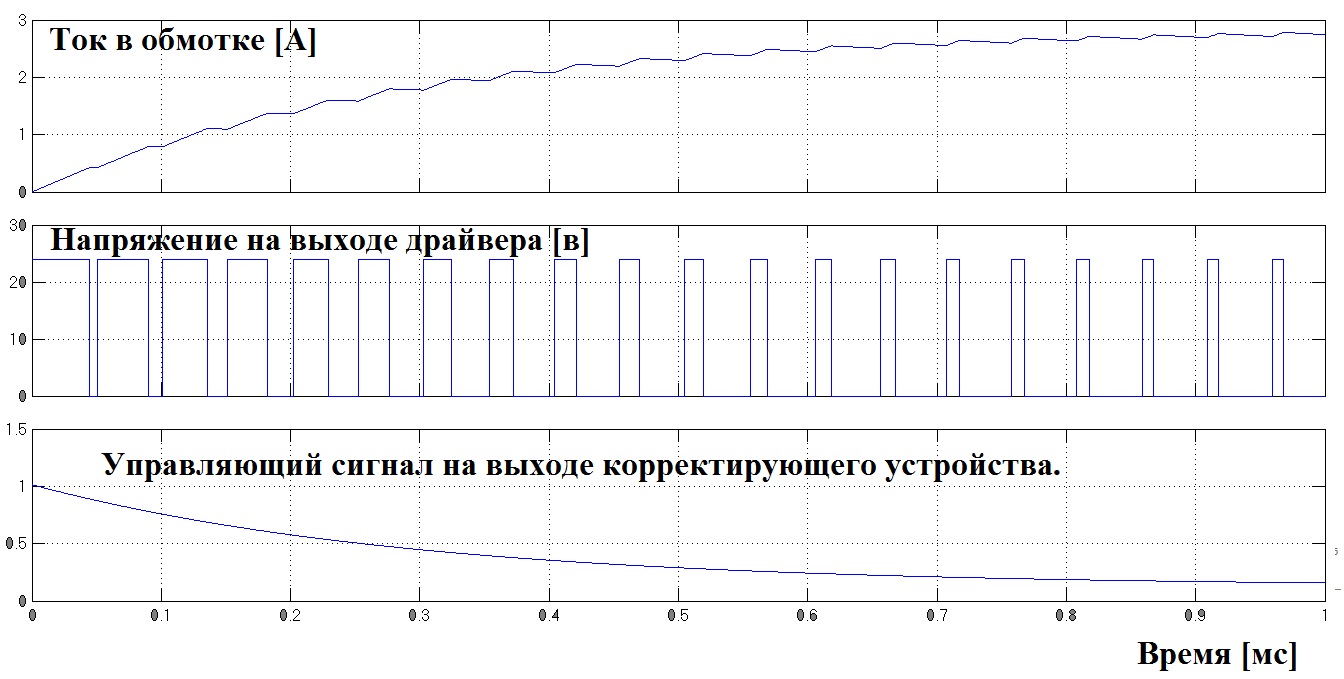
Рис. 2.7.8.
Корректирующее устройство проще всего реализовать в микроконтроллере. Кроме того цифровая или дискретная коррекция весьма интересна с практической точки зрения в силу конструктивной универсальности устройств и гибкости настройки. Чтобы перейти от непрерывной ПФ корректирующего устройства Wк(s) к эквивалентной дискретной Wк(z) необходимо сделать замену:
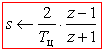
где: Tц - период выполнения программы касательно корректирующего устройства.
В результате получим следующую передаточную функцию:
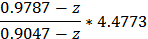
(22)
Чтобы зашить эту функцию в микроконтроллере, нужно реализовать в нём следующий алгоритм (Рис 2.7.9), выполнение которого займёт около 50-ти тактов работы микроконтроллера.
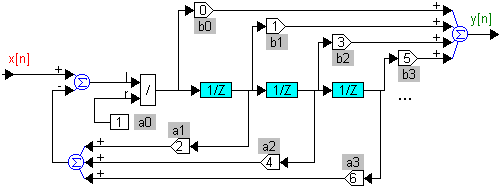
Рис. 2.7.9.
Но как было выше сказано время возрастания/спада не удовлетворяет требованиям к системе, поэтому нужно искать другие, более эффективные методы решения этой задачи.
Использование форсирующего импульса.
В начале каждого шага подаётся 100% - шим того или иного знака, иначе говоря форсирующий импульс, который приводит к быстрому изменению тока. Здесь важно точно рассчитать длительность этого импульса, потому что, если он превысит допустимые пределы ток может вырасти выше номинального в несколько раз, что приведёт к перегоранию обмоток.
Выведем формулу для расчета длительности форсирующего импульса от напряжения питания (U = 24 в) и от тока, который следует получить в результате. В самом общем случае, это не ток, а разность токов между нынешним и будущим током после воздействия импульса. Поэтому обозначим его dI, чтобы подчеркнуть что эта переменная может использоваться как разница токов.
Начнём вывод с общеизвестной функции тока от времени в катушке индуктивности при подключении к источнику напряжения:
|
|
(23)
Далее выводим из формулы время t:
|
|
|
|
|
|
(24)
Вносим полученную формулу и m-файл и реализуем метод на математической модели.
Tf = L*log(U/(U-Inom*(Rd+r)))/(Rd+r)
%время форсирующего импульса [с]
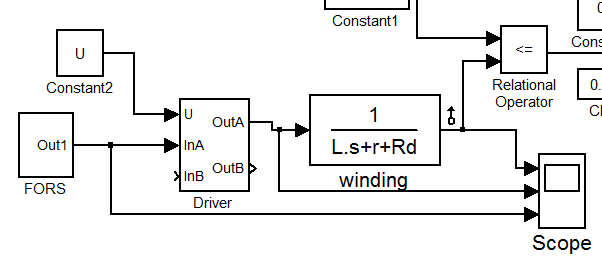
Рис. 2.7.9.
В модели на Рис. 2.7.9 блок FORS формирует форсирующий импульс, требуемой длины. И далее этот сигнал поступает на драйвер. Результаты полученные в результате моделирования:
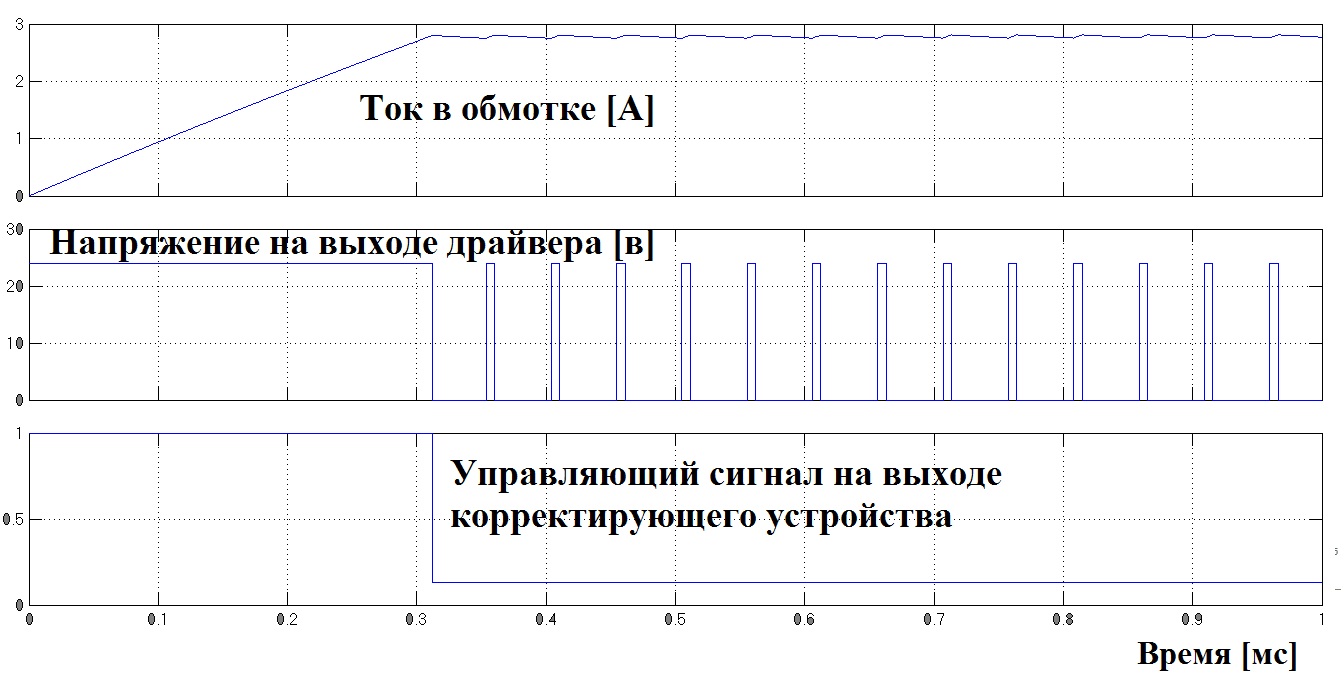
Рис. 2.7.10.
Здесь сигнал, который называется – управляющий сигнал на выходе корректирующего устройства назван так, потому что формирователь форсирующего звена по сути и есть корректирующее звено. Оно может находиться в микроконтроллере в виде затабулированной таблицы. В ней указанны длительности форсирующих импульсов для каждого такта. В результате (см. Рис 2.7.10.) Получаем время нарастания тока 296 мкс, что более чем в 2 раза выше требуемой величины и в несколько раз превышает раннее полученные результаты.
В этой главе было проделано большое количество анализов для различный методов форсирования токов, подведём итоги:
Выводы по выбору способов форсирования токов.
Осветим численные результаты для различных методов. В качестве тестовой задачи требуется увеличить ток в обмотке ШД с нуля до Inom = 2.8 А, имея в наличии источник напряжения 24 в.





















