3. Ia [A] – ток в обмотке A.
4. Ib [A] – ток в обмотке B.
5. Inom [A] – номинальный ток обмотки
6. Va [в] – напряжение, подведённое к обмотки A.
7. Vb [в] – напряжение, подведённое к обмотки B.
8. M [Н*м] – мгновенный момент ШД
9. Ma [Н*м] – составляющая мгновенного момента ШД, как результат действия тока в катушке А
10. Mb [Н*м] – составляющая мгновенного момента ШД, как результат действия тока в катушке В
11. R [ом] – сопротивление каждой из обмоток.
12. L [Гн] – индуктивность каждой из обмоток.
13. Lab [Гн] – взаимоиндукция.
14. p [] – число пар полюсов.
15. Fm [Тл*м^2] – токосцепление от магнита в роторе.
Итак, имеется ШД с 2-мя независимыми обмотками. Их соответственно обозначим: обмотка А и обмотка В. Модель простейшего биполярного двигателя изображен на рисунке 2.3.1.
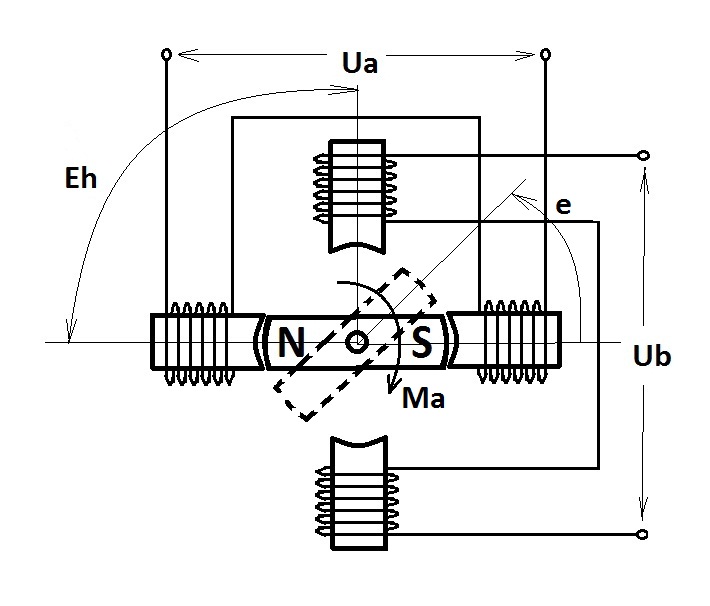
Рис 2.3.1
Обмотки вместе с магнитопроводом образуют статор, а постоянный магнит является ротором. Заметим, что число полюсов ротора является одному. И ещё одно примечание: хотя на рисунке изображено напряжение, поданное на обмотки, мы будем рассматривать ток в этих обмотках, потому что именно он создаёт магнитный поток в магнитопроводах.
Рассмотрим случай, когда подаётся ток только на одну обмотку (A), в таком случае момент выражается следующей формулой:
|
|
(1)
Аналогично для второй обмотки:
|
|
(2)
При наличие токов о обоих обмотках моменты складываются алгебраически (потому что вектора моментов лежат на одной линии). Момент главным образом зависит от тока обмотки и от токосцепления Fm. Токосцеление – это не что иное как магнитный поток вызванный постоянным магнитом ротора. Магнитный поток распределяется по магнитопроводам обмоток А и В согласно гармоническому закону по углу поворота ротора e. Поэтому в формуле появляется синус от e.
На рис. 2.3.1 ротор показанный сплошной линией находится в нулевом положении, т.е. e=0 рад. Если его отклонить на угол e (показано пунктиром) и подать ток в обмотку А, то возникнет момент, стремящийся повернуть ротор в то положение, где магнитный поток в магнитопроводе обмотки А будет максимальным. Или другое объяснение: ротор поворачивается в сторону увеличения магнитного потока. То есть в положение e=0. Момент противоположен отклонению e и поэтому в формулах (1) и (2) ставится минус.
Примечание: даже если магнитный поток от магнита отсутствует, то есть ротор не является магнитом вовсе. В этом случае момент Ma будет иметь не нулевое значение, вопреки формуле (1). Объяснение этому очевидное: индуктивность катушек А и В в зависимости от угла поворота неодинакова, поскольку меняется воздушный зазор между статором и ротором. Нужно ли учитывать этот факт в формулах (1) и (2). Разработчики ШД утверждают что индуктивность обмоток меняется не больше чем на 20% в зависимости от положения ротора, момент главным образом зависит от токосцепления постоянного магнита. Поэтому мы пренебрегли изменением индуктивности L обмоток.
Далее рассмотрим случай, когда ротор свободен от нагрузки. В какое устоявшееся положение повернётся ротор, при подачи на него различных значений токов Ia и Ib .
Воспользуемся формулами (1) и (2), чтобы получить формулу для общего момента ШД:
|
|
(3)
Поскольку, рассматриваем случай, когда момент равен нулю, приравняем его к нулю. В результате получим уравнение устоявшегося положения ротора в зависимости от токов токов Ia и Ib .
|
|
(4)
Вернёмся в уравнению (3). Если обе его части возвести в квадрат, то в последствии можно привести к виду:
|
|
(5)
Обращаем внимание ещё раз на то что это уравнение для максимального статического момента двигателя и для числа пар полюсов на роторе равного двум. Из этого уравнения видно, что для сохранения постоянства момента необходимо соблюдать условие:
|
|
(6)
Условие сохранения момента должно выполняться обязательно. В противном случае это может привести к нежелательным колебаниям или (что ещё хуже) к резонансу в системе.
Наконец изобразим графически уравнение (4), с учётом условия (6):
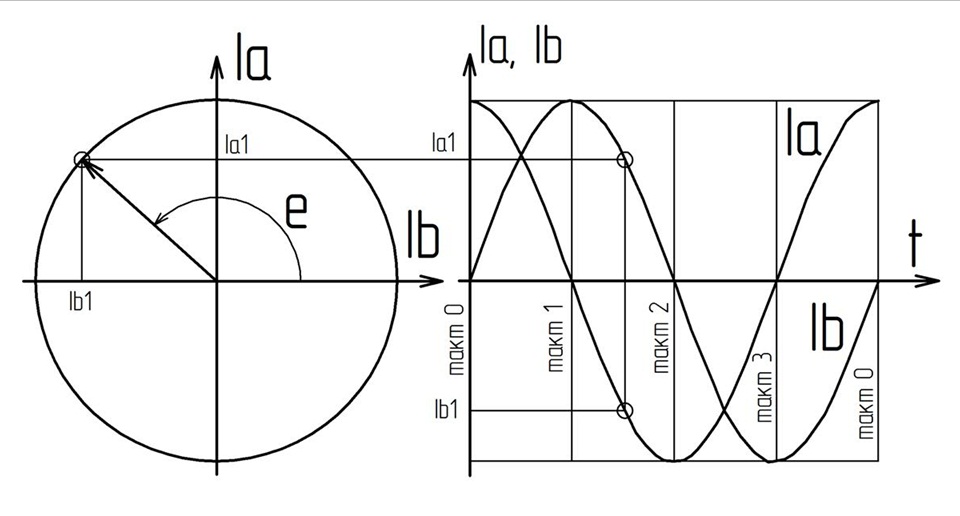
Рис. 2.3.2
Если проводить аналогии с рис.2.3.1, то можно заметить что оси Ia и Ib перпендикулярны осями симметрий соответствующих обмоток. Кроме того направление южного полюса ротора совпадает с направлением вектора на рис. 2.3.2. Это сделано для лучшей понимабельности модели.
Вернёмся к рисунку 2.3.2. Вектор обозначает угол поворота ротора e. Длина вектора пропорциональна максимальному статическому моменту. По осям соответственно откладываются значения токов в обмотках. Точка на координатной плоскости соответствует концу вектора на рис. 2.3.2. При работе двигателя конец вектора будет двигаться по окружности.
Для равномерного вращения ротора с постоянным моментом, необходимо подключить к обмоткам ШД источник тока с синусоидальными сигналами, сдвинутыми по отношению друг к другу на угол Pi/2. Как показано на рисунке 2.3.2 справа от окружности. Для примера так же обозначена точка мгновенных значений токов в момент времени – Ia1 и Ib1.
2. 3. 2 Управление ШД с помощью дискретных сигналов.
Подавать синусоидальные источники токов (как на рис. 2.3.2) – это идеальный способ управления ШД. Но на практике сложно реализовать такие источники, кроме того в некоторые моменты времени нужно остановить ШД, зафиксировав значения токов. Это задача решается с помощью дискретных систем. В них ток меняется не по синусойде, а дискретно (скачкообразно).
В документации на ШД указывается такой параметер как величина полного шага. Что он собственно означает применительно к нашей модели? Для вращения ротора ШД обмотки переключаются в соответствии с некой логикой, таким образом, чтобы с наступлением каждого переключения ШД развивал максимальный момент. При этом он проворачивается на некий угол, который и называется: “величина полного шага” (обозначим её Eh). Легко видеть, что в модели, изображённой на рис. 2.3.1 величина полного шага равна Pi/2.
В следующем таблице указан порядок переключения обмоток в полношаговом режиме:
Таблица 1.
| Такт 0 | Такт 1 | Такт 2 | Такт 3 | |
| Обмотка A | 0 | Inom | 0 | -Inom |
| Обмотка B | Inom | 0 | -Inom | 0 |
Такт – это комбинация токов, которые подаются на обмотку, иначе говоря точка на плоскости Ia,Ib, смотрите рис.2.3.2. В таблице 1 приведён по сути цикл переключений. Для вращения в одном направлении следует переключать такт за тактом, после того как доходим до последнего, начинаем с нулевого такта. Таким образом процесс повторяется циклично. Ротор в модели на Рис.2.3.1 за один цикл сделает полный оборот. Один такт соответствует одному полному шагу в полношаговом режиме. Но при каждом дроблении шагов количество тактов в цикле удваивается. Например в полушаговом режиме такту соответствует ½ полного шага, а всего тактов в цикле 8.
На рис. 2.3.3 изображены на одной шкале времени (в пределах цикла) способы управления ШД в различных режимах: полношаговый, деление шага ½, деление шага ¼ , и так далее. Для наглядности показан только ток Ia, ток другой ток Ib опережает по фазе на Pi/2. При каждом делении шага, частота переключений должна удваиваться, чтобы сохранить скорость вращения ротора ШД.
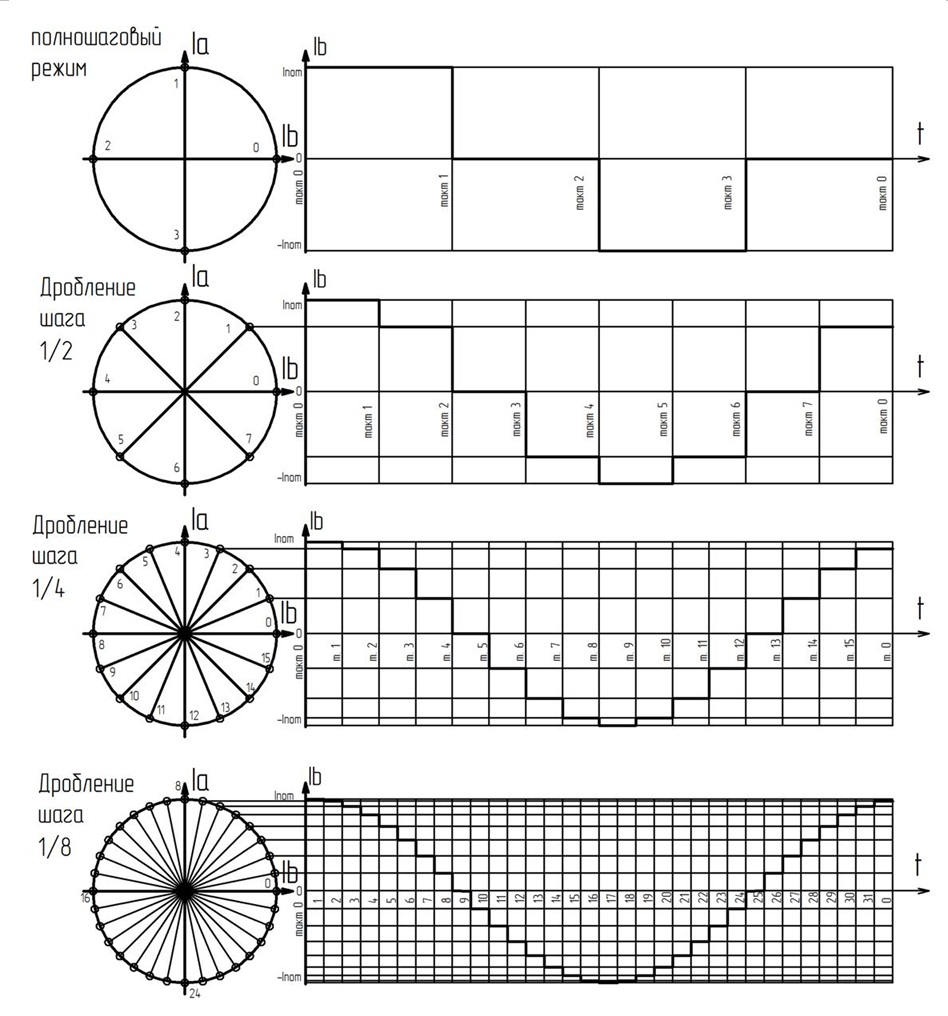
Рис. 2.3.3
2. 3. 3 Добавление к модели электромеханической редукции.
Введём в математическую модель существенный корректив: число пар полюсов на роторе или, что тоже самое, редукцию. Обозначим его p. Для наглядности увеличим изменим модель на рис. 2.3.1 чтобы получить p=2. (рис. 2.3.4)
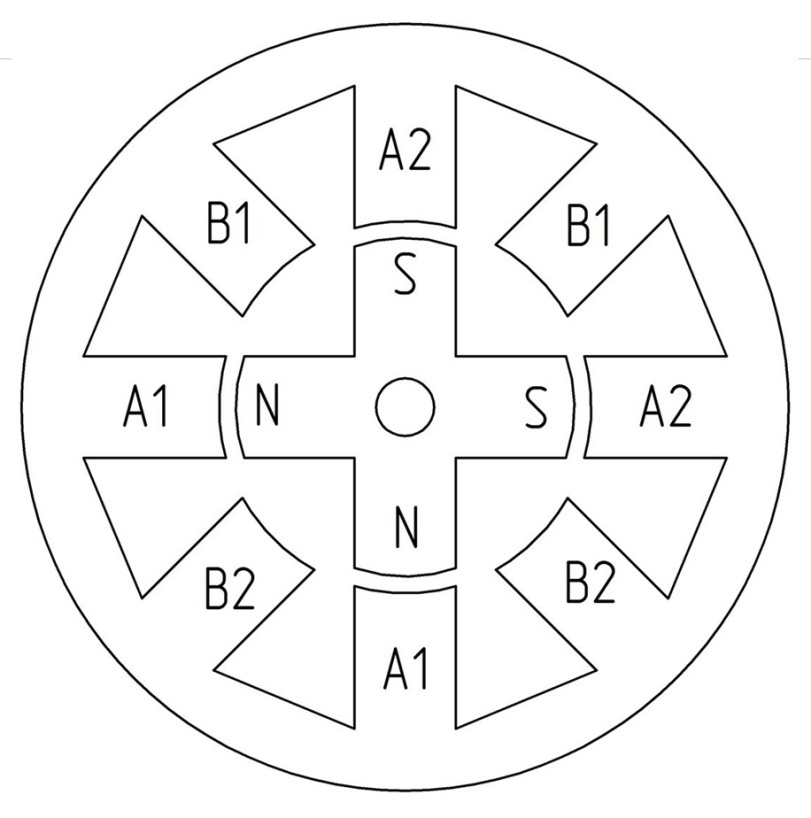
Рис. 2.3.4
Здесь буквами A и B обозначены соответствующие обмотки. Обмотки с разными цифирными обозначениями подключены последовательно друг к другу, а с одинаковыми – запаралелены. Конструктивно ШД выполнены по другому: обмотки и полюса магнитов находятся на разных уровнях, они разнесены (рис. 2.3.5).
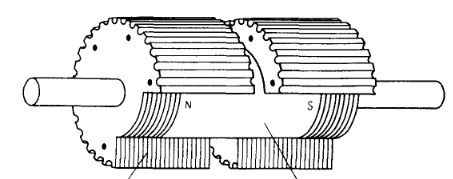
Рис. 2.3.5а (ротор ШД)
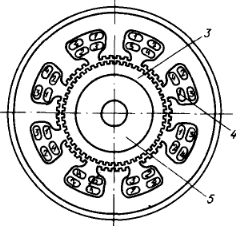
Рис. 2.3.5б (статор ШД)
Зубцы выполняют роль коммутаторов магнитопровода. Когда зубцы статора и ротора установлены друг напротив друга, магнитная проводимость в этом месте максимальна. Она снизится к минимуму если зубцы сдвинуть на величину половины шага зубов. Это позволяет малыми уговыми перемещениями перераспределять магнитный поток в ШД. Но для моделирования ШД лучше воспользуемся моделью на Рис. 2.3.1 и Рис. 2.3.4, поскольку она проще для понимания, а уравнения описывающие обе конструкции абсолютно одинаковы.
Итак, как измениться математическая модель ШД, при введении редукции:
1. Момент, развиваемый ротором ШД увеличится в p раз.
2. Для того чтобы ротор сделал полный оборот, требуется подать p циклов, изображенных на Рис. 2.3.3. Структура тактов не измениться.
В уравнениях эти 2 пункта отразятся следующим образом:
|
|
(7)
|
|
(8)
В паспортных данных обычно дано значение полного шага Eh. Для того чтобы найти редукцию двигателя, воспользуемся простым соотношением:
|
|
(9)
2. 3. 4 Обобщение результатов и получение уравнения ШД.
Уравнение движения ротора.
После того как было получено соотношение для момента мы можем наконец записать уравнение движения ротора в аналитическом виде, с учётом момента инерции ротора и суппорта, а также трения. (стр. 39)
|
|
|
|
(10)
Рассмотрим все слагаемы по порядку:
1. J [кг*м^2] – момент инерции ротора и суппорта (приведённого к радиусу шестерни).
2. Gd [м*Н*с*рад^(-1)] – коэффициент вязкого трения, который учитывает наличие трения в суппорте, а также может быть использован для описания электромагнитых эффектов второго порядка, возникающих из-за гистерезиса и вихревых токов. Зависит от скорости вращения, в некоторых источниках ещё называют динамическое трение.
3. Gs [м*Н] – коэффициент статического трения, не зависит от трения. Сильно возрастает, при обработки платы инструментом: игла.
4. Следующие 2 слагаемых – суммарный момент ротора ШД.
Поскольку мы используем источник напряжения для питания двигателя. Ток не может мгновенно измениться с изменением напряжения. Уравнения для токов в обмотках статора:
|
|
|
|
(11)
(12)
Остановимся на слагаемых обоих уравнениях:
1. Напряжение поданное на соответствующую обмотку.
2. Активное падение напряжения.
3. Противо-ЭДС катушки индуктивности.
4. ЭДС вызванное взаимоиндукцией обмоток.




















