Метрологическая обработка результатов измерений
1. Определим погрешность прибора: Dпр = 0,1 г.
2. Определим наилучшую оценку значений:
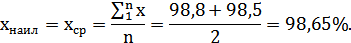
3. Запишем результат в виде:
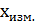 =
= 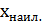 ± ∆
± ∆ 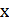
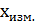 = 98,65 ± 0,1.
= 98,65 ± 0,1.
4. Определим относительную погрешность:
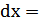
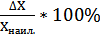 ,
, 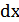 =
= 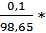 100% = 0,1%
100% = 0,1%
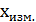 =
= 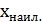 ±
± 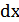 = 98,65 ± 0,1% 9,7 ± 0,1%.
= 98,65 ± 0,1% 9,7 ± 0,1%.
5. Определим размах: R = хmax – xmin, R = 98,8 – 98,5 = 0,3.
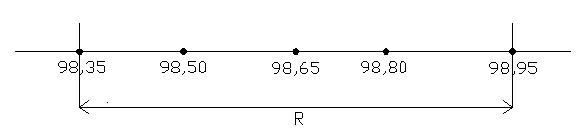
При однократных измерениях число измерений ограничено, поэтому вычисляют не случайную погрешность s, а приближенное значение, которую называют средней квадратической погрешностью, S s.
6. 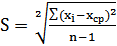 , S =0,21.
, S =0,21.
| n | хi | хср | хср – хi | (хср – хi) 2 |
| 1 | 98,8 |
98,65 | - 0,15 | 0,0225 |
| 2 | 98,5 | 0,15 | 0,0225 | |
| S = 0 | S = 0,045 |
7. Определим суммарную погрешность:
Σ∆ = ∆приб. + ∆мет. + ∆случ. + ∆сист. .
∆приб. = 0,1.
∆мет. 0 - из-за несовершенства метода измерений, некорректности алгоритмов и формул по которым производят вычисления в результатах измерения.
∆случ. = 0,21 ( средняя квадратическая погрешность)
∆сист. согласно РМГ 43-2001 найдем по формуле:
∆сист. 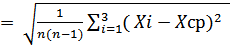 , ∆сист =
, ∆сист = 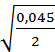 = 0,15.
= 0,15.
Σ∆ = 0,1 + 0 + 0,21 + 0,15 = 0,46.
Самую большую погрешность в измерениях дает случайная погрешность (0,21). Случайные погрешности нельзя исключить из результатов измерений путем введения поправок, однако их можно существенно уменьшить путем увеличения числа единичных измерений. Но это в свою очередь ведет к увеличению затраченного времени экспериментатором на проведение эксперимента.
Заключение
Случайная погрешность измерения – составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины.
В проявлении случайных погрешностей не наблюдается какой-либо закономерности, они обнаруживаются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов. Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результатах измерений. Причин их возникновения множество. В данном случае погрешности вызваны: погрешностью промокательной бумаги, марлевой ткани, геометрии металлического кольца; выбором лабораторных весов по классу точности (специальный, высокий, средний), по виду (механические или электрические, с автоматическим, полуавтоматическим или неавтоматическим уравновешиванием); колебаниями температуры окружающей среды; округлениями показаний СИ.
Значение водоудерживающей способности растворных смесей по ГОСТу 28013-98 должно быть не менее 90%.
Наилучшая оценка – 98,65%.
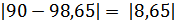
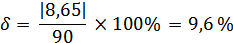
Метрологическая обработка результатов была проведена со средней точностью, которая составляет 9,6%.
Список источников
1. ГОСТ 5802-86. Растворы строительные. Методы испытаний. – М.: Станадартинформ, 2010. – 16 с.
2. ГОСТ 28013-98. Растворы строительные. Общие технические условия. – М.: МНТКС, 1999. – 22 с.
3. Коновалов, А. С. Стандартизация, метрология и сертификация: Учебник / А. С. Коновалов. — М.: Юрайт-Издат, 2005. — 345 с.
4. Методы и способы повышения точности измерений. Часть первая
[Электронный ресурс], – информационный сайт. Режим доступа: http://www.kipia.info/publication – свободный (Дата обращения: 6.12.2015г).








