Геометрический алгоритм Монте-Карло интегрирования

Дата: 2025-05-25; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

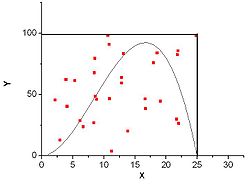
Рисунок 3. Численное интегрирование функции методом Монте-Карло

Для определения площади под графиком функции можно использовать следующий стохастический алгоритм:

• ограничим функцию прямоугольником (n-мерным параллелепипедом в случае многих измерений), площадь которого S_par можно легко вычислить;
• «набросаем» в этот прямоугольник (параллелепипед) некоторое количество точек (N штук), координаты которых будем выбирать случайным образом;
• определим число точек (K штук), которые попадут под график функции;
• площадь области, ограниченной функцией и осями координат, S даётся выражением

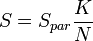
Для малого числа измерений интегрируемой функции производительность Монте-Карло интегрирования гораздо ниже, чем производительность детерминированных методов. Тем не менее, в некоторых случаях, когда функция задана неявно, а необходимо определить область, заданную в виде сложных неравенств, стохастический метод может оказаться более предпочтительным.

Использование выборки по значимости

При том же количестве случайных точек, точность вычислений можно увеличить, приблизив ограничивающую искомую функцию область к самой функции. Для этого необходимо использовать случайные величины с распределением, форма которого максимально близка к форме интегрируемой функции. На этом основан один из методов улучшения сходимости в вычислениях методом Монте-Карло: выборка по значимости.

Оптимизация

Применение в физике

Компьютерное моделирование играет в современной физике важную роль и метод Монте-Карло является одним из самых распространённых во многих областях от квантовой физики до физики твёрдого тела, физики плазмы и астрофизики.

Алгоритм Метрополиса

Традиционно метод Монте-Карло применялся для определения различных физических параметров систем, находящихся в состоянии термодинамического равновесия. Предположим имеется набор W(S) возможных состояний физической системы S. Для определения среднего значения 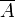некоторой величины A необходимо рассчитать 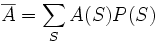, где суммирование производится по всем состояниям S из W(S), P(S) — вероятность состояния S.

Динамическая (кинетическая) формулировка