II. Пустая матрица
Первые шаги работы в пакете Sci Lab
1. Создание вещественных матриц. 1
II. Пустая матрица. 2
III. Определение размера матрицы.. 2
IV. Оператор “:”. 3
V. Динамическое изменение размера матрицы.. 3
VI. Арифметические операции. 4
VII. Операции с матрицами. 4
1. Создание вещественных матриц
1) Ввод матрицы размерностью 3х3:
a=[1 2 3; 2 4 5; 1 0 1]
II. Пустая матрица
III. Определение размера матрицы
Вызов функции size возвращает два параметра nc и nr, значения которых равны числу строк и столбцов в данной матрице.
Пример:
-->d=[2 4 6; 2 3 1]
-->sel="c"
-->sel="r"
-->nr=size(d, sel)
nr = 2.
-->size(d, "*")
ans =6.
2) Ввод матрицы, заданной в алгебраической (символьной) форме: с - свободный столбец.
r=[poly([1 2 3], "x", "c"), 1; poly([1 -1 2], "x", "c"), 2]
3) Ввод матрицы в символьной форме:
x=poly(0, "x");
s=[x, 1+x ; 2-x ,6]
IV. Оператор “:”
Используя вектор индекса, можно обращаться к элементам матрицы в определенных диапазонах строк и столбцов.
Предположим, что необходимо обратиться к элементам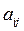 
матрицы m(3х3), причем строка i =3, столбцы j=2 и 3.
Пример:
-->a=[1 5 7; 2 5 9; 0 -1 -2]
-->a(3:3,2:3)
ans = - 1. - 2.
V. Динамическое изменение размера матрицы
Пример: Пусть задана матрица размеров 2х3:
-->d=[1 3 6; 2 4 0]
d =
1. 3. 6.
2. 4. 0.
Увеличим размер матрицы:
-->d(3,1)=7
d =
1. 3. 6.
2. 4. 0.
7. 0. 0.
Удаление 3-ей строки:
-->d(3,:)=[]
Для удаления столбца запись вида: -->d(:, 3)=[]
VI. Арифметические операции
VII. Операции с матрицами
1) Нахождение обратной матрицы: (inverse of matrix) с помощью команды inv.
Синтаксис: inv(Х)
В нашем примере: b=inv(a).
2) Нахождение ранга матрицы: rank (b)
3) Нахождение определителя матрицы: det (b).
4) Создание единичной матрицы: a=eye(3,3) // размерность 3х3.
5) Создание матрицы, состоящей из единиц: a=ones(4,4).
6) Заполнение матрицы случайными числами: d=rand(3,3)
7) Транспонирование матриц.
Транспонирование матриц осуществляется с помощью апострофа (‘),
пример: a=[2 4; 3 -1]’
8) Решение системы уравнений типа А*х + b=0.
Пример: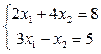 
Запись команд:
a=[2 4; 3 -1]
b=[-8; -5] // или b=[-8 -5]’
[x,kerA]=linsolve(a,b)