Планирование контрольных испытаний на надежность
практическое занятие 8
ПЛАНИРОВАНИЕ КОНТРОЛЬНЫХ ИСПЫТАНИЙ НА НАДЕЖНОСТЬ
Показатель надежности сложной системы является функцией нескольких переменных, характеризующих надежность ее элементов. Многомерные задачи контроля отличаются от приведенных ранее тем, что испытания на надежность в них рассматриваются на уровне элементов системы. При этом связь между показателями надежности элементов и системы в целом предполагается известной и зависит от структурной схемы надежности.
При контроле надежности систем применяют те же методы планирования испытаний и процедуры принятия гипотез, что и при контроле надежности отдельных объектов.
В табл. 8.1 и 8.2, в качестве примеров, приведены формулы для определения объема испытаний и правила приемки при контроле по одному контрольному уровню для систем с типичными ССН.
Таблица 8.1
Объем испытаний для контроля вероятности безотказной работы
при биномиальном плане
| Тип ССН; условия приемки | Число требуемых образцов i-го типа | Примечание |
Последовательная;
| 
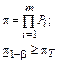
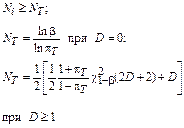
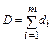|  – суммарное допустимое число отказов;
m – число последовательных элементов
|
Параллельная;
| 
| 
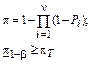
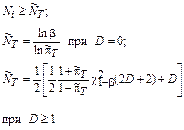
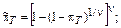ν – число параллельных элементов
|
Таблица 8.2
Объем испытаний для контроля наработки
при экспоненциальном законе распределения
| Тип ССН; условия приемки | Число требуемых образцов i-го типа | Примечание |
Последовательная;
| 
| 
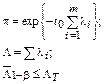
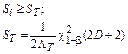
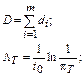t0 – заданная наработка
|
Параллельная;
| 
| 
|
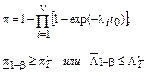
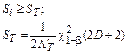
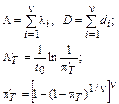
Рассмотрим несколько простых примеров планирования испытаний системы с последовательной и параллельной ССН.
Пример 1. Имеется система с m=10 последовательными разнотипными элементами надежности. Требуемая вероятность безотказной работы πТ=0,90; допустимый риск заказчика β=0,2. Допускается один отказ в ходе испытаний всех элементов. Требуется определить объем испытаний Ni для элементов каждого типа в испытаниях по биномиальному плану [Ni,U,t0].
Решение. Согласно заданным условиям D=1. По табл. 8.1 и таблице c2-распределения находим: χ20,8(4)=6, NT=29.
То есть для каждого элемента требуется провести 29 испытаний. Если бы требуемое число отказов равнялось нулю, тогда NT=ln0,2/ln0,9 = 15,27≈16.
Пример 2. Для системы с последовательной ССН при заданном риске потребителя β=0,10, числе элементов системы m=3, заданных (требуемых) вероятностях безотказной работы элементов Pi – 0,80, 0,90 и 0,99 и нулевом числе допустимых отказов определить требуемое количество испытаний элементов Nт по биномиальному плану.
Решение. Для системы с последовательной ССН при нулевом числе допустимых отказов по формулам табл. 8.1 находим:
, 
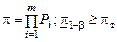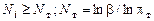, Nт=6,8 (7).
Пример 3. Для систем с параллельной ССН при заданном риске потребителя β=0,10, числе элементов системы ν=2, заданных (требуемых) вероятностях безотказной работы элементов Pi – 0,90 и 0,99 и нулевом числе допустимых отказов определить требуемое количество испытаний элементов по биномиальному плану.
Решение. Для системы с параллельной ССН при нулевом числе допустимых отказов по формулам табл. 8.1 находим:
,
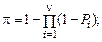
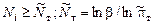
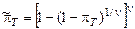Nт=35,9 (36).
задание к контрольной работе 8
Для систем с последовательной и параллельной ССН при заданном риске потребителя β, числе элементов системы m или ν, заданных (требуемых) вероятностях безотказной работы элементов Pi и нулевом числе допустимых отказов di=0 определить требуемое количество испытаний Nт элементов по биномиальному плану.
| Риск потребителя β | Число элементов системы m или ν | Вероятность безотказной работы элемента Pi | Номер варианта |
| Последовательная ССН | |||
| 0,10 | 3 | 0,90; 0,90; 0,90 | 1 |
| 3 | 0,80; 0,90; 0,80 | 2 | |
| 2 | 0,80; 0,80 | 3 | |
| 0,20 | 3 | 0,90; 0,90; 0,80 | 4 |
| 2 | 0,80; 0,80 | 5 | |
| 2 | 0,90: 0,80 | 6 | |
| 3 | 0,80; 0,90; 0,90 | 7 | |
| 0,10 | 3 | 0,80; 0,90; 0,99 | 8 |
| 2 | 0,90; 0,90 | 9 | |
| 2 | 0,99; 0,90 | 10 | |
| Параллельная ССН | |||
| 0,20 | 2 | 0,80; 0,80 | 11 |
| 2 | 0,80; 0,90 | 12 | |
| 3 | 0,80; 0,80; 0,80 | 13 | |
| 3 | 0,99; 0,90; 0,80 | 14 | |
| 0,10 | 3 | 0,90; 0,90; 0,80 | 15 |
| 2 | 0,80; 0,80 | 16 | |
| 2 | 0,90; 0,99 | 17 | |
| 3 | 0,80; 0,99; 0,80 | 18 | |
| 3 | 0,90; 0,90; 0,90 | 19 | |
| 2 | 0,99; 0,95 | 20 | |
ОТВЕТЫ
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Nт(Nфакт) | 7,3 (8) | 4,2 (5) | 5,2 (6) | 3,7 (4) | 3,6 (4) | 3,6 (4) | 3,7 (4) | 6,8 (7) | 10,9(11) | 20 |
| Вариант | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Nт(Nфакт) | 3,6 (4) | 5,2 (6) | 2,4 (3) | 8,9 (9) | 5,7 (6) | 5,2 (6) | 35,9(36) | 10 | 7,3 (8) | 51,1(52) |