Оценка показателей долговечности системы по результатам испытаний элементов
практическое занятие 7
ОЦЕНКА ПОКАЗАТЕЛЕЙ ДОЛГОВЕЧНОСТИ СИСТЕМЫ ПО РЕЗУЛЬТАТАМ ИСПЫТАНИЙ ЭЛЕМЕНТОВ
Расчет точечных и интервальных оценок показателей долговечности может производиться по результатам испытаний или эксплуатации объекта.
Для системы, состоящей из m последовательно соединенных элементов, вероятность безотказной работы каждого из которых Pi, а отказы элементов независимы, показатели долговечности (средняя наработка до отказа и g-процентная наработка до отказа) определяются следующим образом:
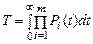 .
.
Подынтегральное произведение представляет собой вероятность безотказной работы за время t системы из m последовательно соединённых элементов. Тγ – корень уравнения:
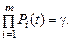
Нижняя доверительная граница гамма-процентной наработки на отказ (или ресурса) при доверительной вероятности q есть корень уравнения
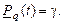
Для распределений с неубывающей интенсивностью отказов (стареющие распределения) оценка снизу определяется при q = =0,5.
Формулы для расчетов показателей долговечности системы по показателям долговечности ее элементов для нескольких наиболее простых случаев приведены в табл. 7.1 и 7.2.
Здесь zq – квантиль распределения вероятности q, т.е. значение аргумента, при котором функция распределения принимает значение, равное q (при нормальном законе распределения квантиль распределения обычно обозначают буквой u); DT – дисперсия точечной оценки ресурса системы.
Таблица 7.1
Оценки среднего ресурса системы по ресурсу элементов
| Функция распределения ресурса i-го элемента | Точечная оценка ресурса | Нижняя доверительная граница ресурса при доверительной вероятности q | Примечание |
| Экспоненциальный | 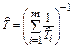
| 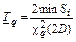
|
|
| Возрастающая функция интенсивности отказов | 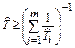
| 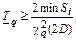
| |
| Произвольный | 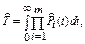
| 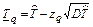
| 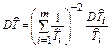
|
Таблица 7.2
Оценка g-процентного ресурса системы
| Функция распределения ресурса i-го элемента | Точечная оценка ресурса | Нижняя доверительная граница ресурса при доверительной вероятности q | Примечание |
| Экспоненциальный | 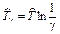
| 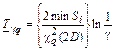
| Si – суммарная наработка |
| Возрастающая функция интенсивности отказов | 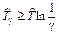
| 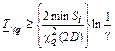
| |
| Произвольный | 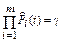 * *
| 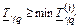
| 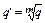 ;
* – точечная оценка ресурса является корнем этого уравнения ;
* – точечная оценка ресурса является корнем этого уравнения
|
задание к контрольной работе 7
Система состоит из m=3 независимых последовательно соединенных элементов. Каждый элемент имеет стареющее распределение ресурса (возрастающая функция интенсивности отказов). В результате испытаний по плану [NiUri] получено: наработка элементов системы ti ч, отказов элементов системы ri. Найти точечные оценки среднего ресурса системы Т и g-процентного ресурса Тγ.
| Номер варианта | ti | ri | γ | ||||
| 1 | 2 | 3 | 1 | 2 | 3 | ||
| 1 | 60 | 50 | 100 | 4 | 5 | 2 | 0,8 |
| 2 | 50 | 60 | 80 | 2 | 3 | 4 | 0,9 |
| 3 | 40 | 40 | 90 | 2 | 2 | 2 | 0,9 |
| 4 | 70 | 70 | 60 | 3 | 4 | 3 | 0,9 |
| 5 | 100 | 50 | 40 | 5 | 2 | 2 | 0,8 |
| 6 | 80 | 40 | 70 | 4 | 2 | 2 | 0,9 |
| 7 | 90 | 70 | 50 | 4 | 4 | 2 | 0,8 |
| 8 | 60 | 100 | 40 | 3 | 6 | 2 | 0,9 |
| 9 | 40 | 80 | 70 | 2 | 5 | 4 | 0,8 |
| 10 | 70 | 90 | 100 | 2 | 3 | 3 | 0,8 |
| 11 | 50 | 60 | 80 | 2 | 3 | 4 | 0,9 |
| 12 | 40 | 40 | 90 | 2 | 2 | 2 | 0,8 |
| 13 | 70 | 70 | 60 | 3 | 4 | 3 | 0,9 |
| 14 | 100 | 50 | 40 | 6 | 2 | 3 | 0,9 |
| 15 | 80 | 70 | 70 | 4 | 4 | 3 | 0,8 |
| 16 | 90 | 100 | 50 | 5 | 5 | 4 | 0,9 |
| 17 | 60 | 80 | 70 | 3 | 4 | 4 | 0,8 |
| 18 | 80 | 90 | 100 | 3 | 4 | 5 | 0,9 |
| 19 | 70 | 60 | 80 | 4 | 3 | 3 | 0,9 |
| 20 | 50 | 60 | 90 | 2 | 4 | 5 | 0,8 |
Пример решения для варианта № 1:
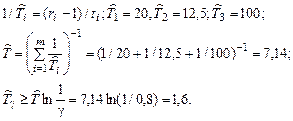
Усложненный вариант выполнения контрольной работы содержит оценку нижней доверительной границы ресурса при доверительной вероятности q (для такой оценки нужны таблицы χ2-распределения):
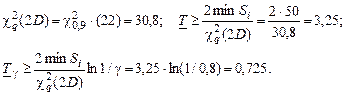
ОТВЕТЫ
| Номер варианта | T, ч | Tγ, ч | Номер варианта | T, ч | Tγ, ч |
| 1 | 7,14 | 1,6 | 11 | 11 | 1,2 |
| 2 | 11 | 1,2 | 12 | 16,4 | 3,7 |
| 3 | 16,4 | 1,7 | 13 | 9,5 | 1 |
| 4 | 9,5 | 1 | 14 | 8,3 | 0,9 |
| 5 | 11,8 | 2,6 | 15 | 9,2 | 2 |
| 6 | 13 | 1,4 | 16 | 6,9 | 0,7 |
| 7 | 10,4 | 2,3 | 17 | 8,8 | 2 |
| 8 | 9,2 | 1 | 18 | 10,2 | 1,1 |
| 9 | 8,5 | 1,9 | 19 | 9,9 | 1 |
| 10 | 17,7 | 4 | 20 | 8,7 | 2 |