Оценка безотказности системы по результатам

Дата: 2025-05-25; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

практическое занятие 6

 

ОЦЕНКА БЕЗОТКАЗНОСТИ СИСТЕМЫ ПО РЕЗУЛЬТАТАМ

БИНОМИНАЛЬНЫХ ИСПЫТАНИЙ ЭЛЕМЕНТОВ

 

Точечные оценки показателей надежности рассмотрены в ПЗ 3. Интервальные оценки целесообразны в условиях небольшой статистики и неизвестных законах распределения параметров (в последнем случае, к тому же, испытания считаются проведенными по биномиальному плану).

Формулы вычисления интервальных оценок показателей надежности непараметрическим методом приведены в табл. 6.1, а при экспоненциальном законе распределения – в табл. 6.2.

 

Таблица 6.1

Показатель надежности Нижняя доверительная граница при доверительной вероятности q Верхняя доверительная граница при доверительной вероятности q
Средняя наработка до отказа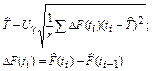
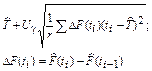
Гамма-процентная наработка до отказа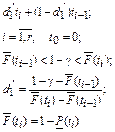
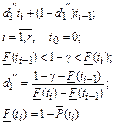
Вероятность безотказной работы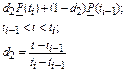

 

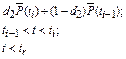
Из табл. 6.1 видно, что в оценках используется квантиль нормального распределения Uγ. Это связано с тем, что при неизвестном законе распределения приблизительные оценки делаются непараметрическим методов в предположении нормального закона распределения.

Формулы вычисления интервальных оценок показателей надежности при других известных законах распределения и их параметров в различных планах испытаний приведены в справочниках.

Таблица 6.2

Интервальные оценки показателей надежности при

экспоненциальном законе распределения

Показатель надежности

Доверительная граница при доверительной вероятности q
Нижняя граница Верхняя граница
Средняя наработка до отказа (на отказ), средний ресурс (срок службы, срок сохраняемости, время восстановления)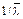
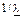
Гамма-процентный ресурс (срок службы, срок сохраняемости)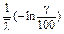
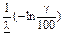
Вероятность безотказной работы за наработку t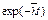
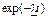
Интенсивность отказов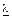

 

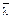
Системы с последовательной ССН состоят из нескольких последовательно соединенных элементов, вероятность безотказной работы каждого из которых неизвестна. Отказы элементов независимы. Каждый i-й элемент как бы проходит Ni автономных испытаний по биномиальному плану с регистрацией числа отказов li.

По результатам испытаний каждого элемента находят γ-нижнюю границу 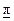для вероятности безотказной работы системы на интервале времени [0, t0], т.е. для заданной доверительной вероятности γ выполняется неравенство P( 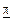)≥γ.

Даже при таких упрощенных условиях решение задачи неоднозначно. Один из практических методов решения состоит в следующем. По результатам испытаний каждого элемента оценивают показатель безотказности – вероятность безотказной работы. Применяя для системы с последовательной ССН теорему умножения вероятностей, вычисляют оценку вероятности безотказной работы системы. Используя соотношения, справедливые для биномиальных испытаний, вычисляют оценку вероятности отказа системы, по которой находят нижнюю границу вероятности безотказной работы системы для заданной доверительной вероятности:

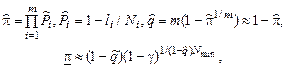
где Nmin – минимальное число испытаний из всех Ni.

 

задание к контрольной работе 6

 

Система состоит из m последовательно соединенных элементов, вероятность безотказной работы каждого из которых Pi неизвестна. Отказы элементов независимы. Каждый i-й элемент как бы проходит Ni автономных испытаний по биномиальному плану с регистрацией числа отказов li. Испытания проводят в номинальном режиме без остановок. По результатам испытаний каждого элемента требуется найти оценки среднего значения π и γ – нижней границы 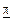для вероятности безотказной работы системы на заданном интервале времени.

 

Номер варианта

m

Ni

li

γ
1 2 3 1 2 3
1 3 10 20 10 3 4 3 0,9
2 2 20 10 - 3 4 - 0,8
3 2 20 20 - 3 5 - 0,95
4 2 20 10 - 3 4 - 0,9
5 2 20 20 - 3 5 - 0,95
6 2 10 10 - 2 3 - 0,9
7 2 10 20 - 2 5 - 0,95
8 3 10 20 20 2 5 4 0,9
9 3 10 10 20 2 3 4 0,8
10 3 10 20 20 2 6 4 0,8
11 3 10 10 20 2 3 4 0,9
12 3 10 20 10 2 2 4 0,85
13 2 20 10 - 3 4 - 0,9
14 2 10 20 - 3 4 - 0,9
15 2 10 10 - 3 2 - 0,8
16 2 10 20 - 3 2 - 0,85
17 3 10 10 10 3 5 2 0,8
18 3 20 20 10 2 5 2 0,95
19 3 20 10 10 2 6 2 0,9
20 3 20 20 10 2 5 2 0,9

Для выполнения контрольного задания целесообразно применить указанный выше метод решения.

 

ОТВЕТЫ

 

Вариант 1 2 3 4 5 6 7 8 9 10
π 0,39 0,51 0,64 0,51 0,64 0,56 0,60 0,48 0,45 0,45
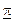
0,06 0,29 0,46 0,25 0,46 0,31 0,32 0,18 0,17 0,17
Вариант 11 12 13 14 15 16 17 18 19 20
π 0,45 0,43 0,51 0,56 0,56 0,63 0,28 0,54 0,29 0,54
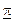
0,14 0,13 0,25 0,31 0,36 0,45 0 0,28 0 0,26