Расчет показателей безотказности системы

Дата: 2025-05-25; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

практическое занятие 5

РАСЧЕТ ПОКАЗАТЕЛЕЙ БЕЗОТКАЗНОСТИ СИСТЕМЫ

ПО РЕЗУЛЬТАТАМ ИСПЫТАНИЙ ЭЛЕМЕНТОВ

Расчетно-экспериментальные методы применяют для оценки надежности объекта по известной надежности его элементов и составных частей (основная или основная и дополнительная информация), а также при наличии основной и дополнительной информации об объекте в целом. Для реализации метода по информации о составных частях необходимо на основе структурной схемы надежности составить функцию связи показателя надежности объекта с показателями надежности его составных частей. После этого следует вычислить точечные и/или интервальные оценки показателей надежности составляющих элементов и путем подстановки их в функцию связи – показатель надежности объекта.

При наличии основной и дополнительной информации об объекте показатели надежности вычисляют параметрическими и непараметрическими методами. Основной обычно считают информацию об оцениваемом объекте, а дополнительной – об объектах-аналогах. В параметрических методах однородность основной и дополнительной информации об объекте и условиях его работы характеризуют коэффициентом, представляющим собой отношение параметров распределений для основной и дополнительной информации (табл. 5.1). В зависимости от значения этого коэффициента различают четыре типовые ситуации (ТС) (табл. 5.2).

Таблица 5.1

Коэффициенты отношения параметров распределений

Закон распределения	Известный параметр	Коэффициент K_j=
Экспоненциальный	—	λ_o/λ_j
Нормальный	σ_j	μ_j/μ_o
Логарифмически нормальный	σ_j	μ_j/ρ_o
Вейбулла	b_j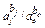

Примечание. Индексы «j» и «о» обозначают объект-аналог и оцениваемый объект соответственно.

Таблица 5.2

Типовые ситуации

Обозначение ТС	Описание ТС	Информация о K_j
ТС-1	Однотипные объекты в одинаковых условиях, их показатели надёжности одинаковы	K_j=1
ТС-2	Однотипные объекты в разных условиях, известны коэффициенты K_j	K_j известно
ТС-3	Однотипные объекты в разных условиях, известны диапазоны изменения K_j для разных условий работы	K_j_max ≥ K_j ≥ ≥ K_j_min
ТС-4	Однотипные объекты в разных условиях, известно, как меняются K_j в зависимости от условий	K_j≥ или ≤ 1

Применяя непараметрические методы, полагают следующее:

· виды законов распределений наработки объекта и аналога неизвестны;

· условия работы объекта и аналога одинаковые;

· номенклатура показателей надежности объекта и аналога полностью совпадают.

Вообще расчетно-экспериментальные методы анализа надежности систем разнообразны и довольно сложны. Детализация и тем более освоение их не входит в задачи настоящего курса. Мы рассмотрим их применение на относительно простых примерах определения показателей надежности систем с последовательной структурной схемой надежности (ССН), т.е. с последовательным соединением элементов надежности. Система с последовательным соединением, во-первых, наименее надежна, и, во-вторых, к ней, в конечном счете, сводятся все остальные более сложные схемы.

В случае оценки показателей безотказности систем с последовательной ССН при планах испытаний с измерением наработки до отказа известны план испытаний и вид закона распределения (или его класс) наработки до отказа i-го элемента. Из всех возможных ситуаций рассмотрим наиболее «определимую», а именно: все элементы испытываются по одному и тому же плану, закон распределения показателей безотказности для всех элементов один и тот же, неизвестны лишь его параметры, есть данные о наработках до отказа или цензурирования каждого из элементов системы.

По этим данным оценивают неизвестные параметры закона распределения наработки до отказа каждого элемента, а затем находят точечные и интервальные оценки вероятности безотказной работы системы с последовательной ССН.

Рассмотрим случай экспоненциального закона распределения наработки до отказа. При этом выберем наиболее простую систему – систему, состоящую из n последовательно соединенных однотипных элементов (типовая ситуация ТС-1). Вероятность безотказной работы такой системы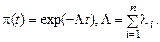

Точечные и интервальные оценки вероятности безотказной работы системы находят по соотношениям:

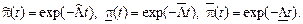
Формулы для точечных и интервальных оценок параметра Λ приведены в табл. 5.3.

Таблица 5.3

Оценка параметра Λ

План испытаний	Точечная оценка	Доверительная граница		Примечание
План испытаний	Точечная оценка	нижняя	верхняя
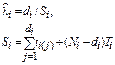
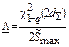
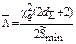
[N_iUT_i]				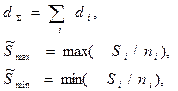при одной группе однотипных элементов n_i=1
[N_iUr_i]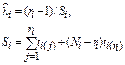

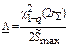
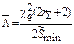
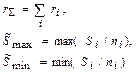
задание к контрольной работе 5

Система состоит из последовательно соединенных однотипных элементов (типовая ситуация ТС-1, число групп однотипных элементов n =1). Вычислить оценки вероятности безотказной работы (точечную и доверительные границы при доверительной вероятности q) при исходных данных:

· число последовательных элементов в системе i;

· испытания элементов проведены по плану [N_iUT_i] или [N_iUr_i] согласно варианту;

· объем испытаний N_i, число отказов r_i или d_i по группам элементов i, время наработки до отказа t_i и время испытаний Т_i (приведены в таблице вариантов);

· закон распределения показателя надежности экспоненциальный;

· наработка для оценки показателя надежности t₀ часов.

Варианты

Номер варианта	План испытаний	Число групп однотипных элементов n	N_i i=			r_i или d_i i=			t_i i=			t₀/q
Номер варианта	План испытаний	Число групп однотипных элементов n	1	2	3	1	2	3	1	2	3	t₀/q
1	[N_iUT_i]	1	5	8	-	2	3	-	5; 7 T₁=10	5; 6; 9 T₂=10	-	10/0,9
2	[N_iUT_i]	1	5	8	-	2	3	-	5; 7 T₁=10	5; 6; 9 T₂=10	-	8/0,9
3	[N_iUT_i]	1	5	8	-	2	3	-	5; 7 T₁=10	5; 6; 9 T₂=10	-	6/0,9
4	[N_iUT_i]	1	5	7	-	2	3	-	5; 7 T₁=8	5; 6; 9 T₂=10	-	10/0,9
5	[N_iUT_i]	1	5	7	-	2	3	-	5; 7 T₁=10	5; 6; 9 T₂=10	-	6/0,9
6	[N_iUr_i]	1	5	8	-	2	3	-	4,5; 6,5 T₁=10	5; 6; 9 T₂=10	-	10/0,9
7	[N_iUr_i]	1	5	8	-	2	3	-	4,5; 6,5 T₁=10	5; 6; 9 T₂=10	-	8/0,9
8	[N_iUr_i]	1	5	8	-	2	3	-	4,5; 6,5 T₁=10	5; 6; 9 T₂=10	-	6/0,9
9	[N_iUr_i]	1	5	7	-	2	3	-	4,5; 6,5 T₁=8	5; 6; 9 T₂=10	-	10/0,9
10	[N_iUr_i]	1	5	7	-	2	3	-	4,5; 6,5 T₁=10	5; 6; 9 T₂=10	-	6/0,9
11	[N_iUT_i]	1	5	8	12	2	3	4	5; 7 T₁=10	5; 6; 9 T₂=10	4; 6; 7; 9 Т₃=12	10/0,9
12	[N_iUT_i]	1	5	8	12	2	3	4	5; 7 T₁=10	5; 6; 9 T₂=10	4; 6; 7; 9 Т₃=12	8/0,9
13	[N_iUT_i]	1	5	8	12	2	3	4	5; 7 T₁=10	5; 6; 9 T₂=10	4; 6; 7; 9 Т₃=12	6/0,9
14	[N_iUT_i]	1	5	7	11	2	3	3	5; 7 T₁=8	5; 6; 9 T₂=10	4; 6; 7 Т₃=12	10/0,9
15	[N_iUT_i]	1	5	7	11	2	3	3	5; 7 T₁=10	5; 6; 9 T₂=10	4; 6; 7 Т₃=12	6/0,9
16	[N_iUr_i]	1	5	8	12	2	3	3	6; 8 T₁=8	5; 6; 10 T₂=10	5; 7; 8 Т₃=8	10/0,9
17	[N_iUr_i]	1	5	8	12	2	3	4	6; 8 T₁=8	5; 6; 10 T₂=10	4; 6; 7; 12 Т₃=12	8/0,9
18	[N_iUr_i]	1	5	8	12	2	3	4	6; 8 T₁=8	5; 6; 10 T₂=10	4; 6; 7; 12 Т₃=12	6/0,9
19	[N_iUr_i]	1	5	7	11	2	3	3	6; 9 T₁=9	5; 6; 10 T₂=10	4; 6; 11 Т₃=11	10/0,9
20	[N_iUr_i]	1	5	7	11	2	3	3	6; 9 T₁=9	5; 6; 10 T₂=10	4; 6; 11 Т₃=11	6/0,9

Решение. Вероятность безотказной работы системы

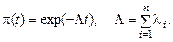
Точечные и интервальные оценки вероятности безотказной работы системы находят по соотношениям: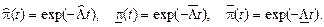

Формулы для расчета параметра Λ см. в табл. 5.3.

Пример расчета для варианта № 1:

S₁=5+7+10(5-2)=42 ч, λ₁=2/42=0,0476,

S₂=5+6+9+10(8-3)=70 ч, λ₂=3/70=0,0429,

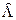=0,0476+0,0429=0,0905.

Для q = 0,9 и d_Σ = 2+3=5 по таблицам для квантилей χ²-распределения находим:

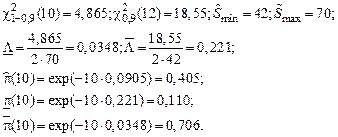
ОТВЕТЫ

Номер варианта	Вероятность безотказной работы
Номер варианта	Средняя	Нижняя граница	Верхняя граница
1	0,405	0,110	0,706
2	0,468	0,171	0,757
3	0,581	0,266	0,812
4	0,348	0,0760	0,667
5	0,557	0,266	0,784
6	0,589	0,104	0,706
7	0,654	0,164	0,757
8	0,728	0,258	0,812
9	0,538	0,0707	0,667
10	0,690	0,255	0,784
11	0,291	0,109	0,818
12	0,376	0,0669	0,700
13	0,477	0,132	0,766
14	0,267	0,027	0,662
15	0,475	0,157	0,781
16	0,467	0,037	0,603
17	0,534	0,050	0,706
18	0,624	0,106	0,770
19	0,473	0,0455	0,652
20	0,638	0,157	0,774

Для справки:

Параметр	Х=10	Х=12	Х=16	Х=18	Х=20
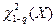
	4,865		9,31	10,865
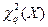
		18,55		25,989	28,412