Оценка остаточного ресурса по результатам
Контрольная работа №4
ОЦЕНКА ОСТАТОЧНОГО РЕСУРСА ПО РЕЗУЛЬТАТАМ
ИСПЫТАНИЙ ПАРТИИ ИЗДЕЛИЙ
Задача оценки остаточного ресурса актуальна потому, что расчетный ресурс, как правило, определен с запасом. Техническое устройство, таким образом, может эксплуатироваться и после исчерпания назначенного ресурса. Поэтому, с точки зрения эффективности использования, целесообразно иметь более реалистичные данные о ресурсе технического устройства.
Точечная оценка среднего остаточного ресурса по результатам испытаний N объектов, не достигших предельного состояния, определяется выражением:
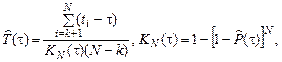 (4.1)
(4.1)
где N – объем выборки; τ – наработка, для которой определяется остаточный ресурс; k – количество отказавших объектов на интервале наработки (0, τ).
Формулы для расчета доверительных границ остаточного ресурса приведены в справочной литературе.
задание к контрольной работе 4
Определить непараметрическим методом вероятность безотказной работы P(τ) на интервале времени (0, τ) и средний остаточный ресурс объекта T(τ) после наработки в течение τ часов при условиях: испытано N объектов, их наработки до отказов ti, ч.
| Номер варианта | N | ti, ч | τ, ч |
| 1 | 10 | 250, 12050, 12500, 14100, 14450, 16050, 17100, 18950, 19200, 19700 | 10000 |
| 2 | 10 | 250, 2050, 12500, 14100, 14450, 16050, 17100, 18950, 19200, 19700 | 10000 |
| 3 | 10 | 250, 6050, 9500, 14100, 14450, 16050, 17100, 18950, 19200, 19700 | 10000 |
| 4 | 10 | 500, 12050, 12500, 14100, 14450, 16050, 17100, 18500, 19000, 19500 | 10000 |
| 5 | 10 | 500, 6050, 12500, 14100, 14450, 16050, 17100, 18500, 19000, 19500 | 10000 |
| 6 | 10 | 3000, 6050, 7500, 8500, 9100, 9900, 17000, 18500, 19000, 19500 | 10000 |
| 7 | 8 | 1000, 8050, 8500, 9000, 9500, 10000, 10500, 11000 | 8000 |
| 8 | 8 | 1000, 6050, 8500, 9000, 9500, 10000, 10500, 11000 | 8000 |
| 9 | 8 | 1000, 6000, 7500, 9000, 9500, 10000, 10500, 11000 | 8000 |
| 10 | 8 | 3000, 6000, 8300, 8900, 9500, 10000, 10500, 11000 | 9000 |
| 11 | 8 | 4000, 6000, 8000, 8500, 9500, 10000, 10500, 10700 | 9000 |
| 12 | 8 | 800, 5000, 7500, 9000, 9500, 10000, 10500, 11000 | 8000 |
| 13 | 6 | 1000, 6100, 6500, 7000, 7500, 8000 | 6000 |
| 14 | 6 | 1000, 2000, 6500, 7000, 7500, 8000 | 6000 |
| 15 | 6 | 1000, 3000, 5500, 7000, 7500, 8000 | 6000 |
| 16 | 6 | 1000, 6100, 7000, 7500, 8500, 9000 | 6000 |
| 17 | 6 | 1000, 5900, 7000, 8000, 9000, 10000 | 6000 |
| 18 | 6 | 1000, 4000, 5000, 7000, 7500, 8000 | 6000 |
| 19 | 6 | 1000, 5900, 7000, 8000, 9000, 10000 | 4000 |
| 20 | 6 | 1000, 3000, 5500, 7000, 7500, 8000 | 6000 |
Пример решения для варианта № 1.
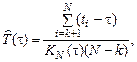
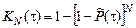 ,
,
где N = 10, t=10000, k = 1 – число отказавших объектов на интервале (0, t), а
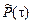 = 1–1/10 = 0,90 - находят непараметрическим методом.
= 1–1/10 = 0,90 - находят непараметрическим методом.
Оценка вероятности безотказной работы за время t определяется линейной интерполяцией в интервале (t i; ti-1):
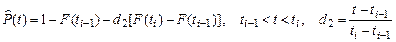 , где вероятность отказа при наработке t i определяют непараметрическим методом:
, где вероятность отказа при наработке t i определяют непараметрическим методом:
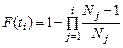 .
.
Вычислим остаточный ресурс после наработки в течение τ часов:
KN=1–(0,1)10 » 1;
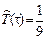 (2050+2500+4100+4450+6050+7100+8950+9200+9700)=6011 ч.
(2050+2500+4100+4450+6050+7100+8950+9200+9700)=6011 ч.
Примечание. Если бы мы оценивали по тем же результатам испытаний среднюю наработку до отказа непараметрическим методом, то она была бы равна: 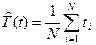 =14440 ч, а у нас уже получилось не менее 10000+6011=16011 ч.
=14440 ч, а у нас уже получилось не менее 10000+6011=16011 ч.
ОТВЕТЫ
| Номер варианта | k | P(τ) | KN | T(τ), ч |
| 1 | 1 | 0,817 | 1 | 6010 |
| 2 | 2 | 0,724 | 1 | 6510 |
| 3 | 3 | 0,689 | 1 | 7080 |
| 4 | 1 | 0,818 | 1 | 5920 |
| 5 | 2 | 0,739 | 1 | 6400 |
| 6 | 6 | 0,386 | 0,99 | 8590 |
| 7 | 1 | 0,751 | 1 | 1520 |
| 8 | 2 | 0,65 | 1 | 1750 |
| 9 | 3 | 0,583 | 1 | 2000 |
| 10 | 4 | 0,48 | 0,995 | 1260 |
| 11 | 4 | 0,44 | 0,99 | 1190 |
| 12 | 3 | 0,583 | 1 | 2000 |
| 13 | 1 | 0,669 | 1 | 1020 |
| 14 | 2 | 0,52 | 0,99 | 1260 |
| 15 | 3 | 0,444 | 0,97 | 1550 |
| 16 | 1 | 0,67 | 1 | 1620 |
| 17 | 2 | 0,65 | 1 | 2500 |
| 18 | 3 | 0,42 | 0,96 | 1560 |
| 19 | 1 | 0,73 | 1 | 3980 |
| 20 | 3 | 0,44 | 0,97 | 1550 |








