Экспериментальные методы исследования надежности
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 3
ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ НАДЕЖНОСТИ
3.2. Оценка показателей надежности экспериментальными методами
Различают параметрический и непараметрический методы экспериментальной оценки показателей надежности.
Непараметрический метод – непосредственная оценка показателя надежности при неизвестном законе распределения.
Параметрический метод – оценка показателя надежности по вычисленным параметрам распределения показателя при известном законе распределения.
Параметрические методы применяют при нормальном, экспоненциальном, логарифмически нормальном, диффузионном распределениях и при распределении Вейбулла.
Точечную оценку непараметрическим методом вычисляют при r > 5. При меньших значениях используют нижние доверительные границы показателей надежности. Для планов без восстановления и замены объектов последовательность вычисления показателей следующая: полученные экспериментально наработки до отказов и до цензурирования выстраивают в вариационный ряд в порядке возрастания; вычисляют оценку интегральной функции распределения
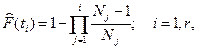 (3.1)
(3.1)
где Nj – количество работоспособных изделий до j-го отказа в вариационном ряду.
Для планов [NUT], [NUN], [NUr]
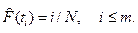 (3.2)
(3.2)
Здесь m=d для планов [NUT], [NMT] и [NRT] и m=r для планов [NUr], [NMr] и [NRr].
Формулы вычисления точечных оценок показателей надежности для некоторых планов испытаний приведены в табл. 3.1.
Таблица 3.1
Формулы для вычисления значений точечных оценок
показателей надежности
| План испытаний | Средняя наработка до отказа, средний ресурс (срок службы, срок сохраняемости, время восстановления) | Гамма-процентная наработка, гамма-процентный ресурс (срок службы, срок сохраняемости) | Вероятность безотказной работы за наработку t |
| [NUN] | 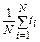
|
где 1-γ/100 – регламентированная вероятность |
|
| [NUr] [NUT] | 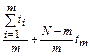
|
Точечная оценка параметрическим методом. Формулы для вычисления точечных оценок показателей надежности для некоторых законов распределения приведены в табл. 3.2.
Для оценки показателя надежности необходимо вычислить точечные оценки параметров распределения. Формулы вычисления точечной оценки параметра λ экспоненциального распределения приведены в табл. 3.2.
Формулы вычислений параметров для других законов распределения можно найти в справочниках по надежности.
Таблица 3.2
Формулы для вычисления значений точечных оценок показателей
надежности при известном законе распределения
| Закон распределения | Средняя наработка до отказа, средний ресурс (срок службы, срок сохраняемости, время восстановления) | Гамма-процентная наработка, гамма-процентный ресурс (срок службы, срок сохраняемости) | Вероятность безотказной работы за наработку t |
Экспоненциальный
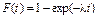
| 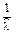
| 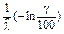
| 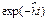
|
Нормальный
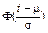
| 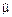
| 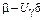
| 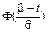
|
Вейбулла
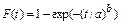
| 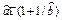
| 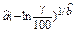
| 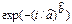
|
Таблица 3.3
Точечные оценки параметра λ экспоненциального распределения
| План испытаний | Оценка параметра λ |
| [NUN] | 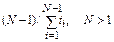
|
| [NUr] | 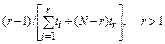
|
| [NUT], | 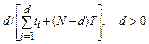
|
| [NUz] | 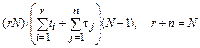
|
| [NMr] | 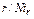
|
| [NMT] | d/NT |
ЗАДАНИЕ К КОНТРОЛЬНОЙ РАБОТЕ 3
Проведены испытания N образцов. Произошло r отказов (план испытаний [NUr]). Наработки до отказа равны ti. Определить среднюю наработку до отказа, если закон распределения наработки экспоненциальный.
Варианты
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| N | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 20 | 20 | 20 |
| r | 5 | 4 | 6 | 3 | 8 | 7 | 5 | 5 | 7 | 8 |
| ti | 4 5 6 7 8 | 4 5 6 6,2 | 3 3,4 4,5 5 5,5 6 | 8 9 10 | 3 3,5 4 4,5 4,8 5 5,2 5,7 | 3,5 4 4,5 4,8 5 5,2 5,7 | 4,5 4,8 5 5,2 5,7 | 4,5 4,8 5 5,2 5,7 | 3 3,5 4 4,5 4,8 5 5,2 | 3 3,5 4 4,5 4,8 5 5,2 5,7 |
| Вариант | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| N | 20 | 20 | 20 | 20 | 25 | 25 | 25 | 25 | 25 | 25 |
| r | 3 | 6 | 4 | 5 | 4 | 6 | 3 | 2 | 7 | 5 |
| ti | 2 3 4 | 4 4,5 4,8 5 5,2 5,7 | 4 4,5 5 5,5 | 4 4,5 5 5,5 6 | 5 5 5,5 6 | 4 4,5 4,8 5 5,5 6 | 6 7 8 | 6 7 | 3 3,5 4 4,5 4,8 5 5,2 | 5 5,5 5,6 5,8 6 |
Решение. При экспоненциальном законе распределения средняя наработка до отказа: Т0=1/λ, где λ – интенсивность отказов. При избранном плане испытаний
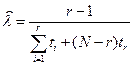 ,
, 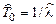 .
.
ОТВЕТЫ
| Варианты | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| λ | .0174 | .0164 | .0292 | .0067 | .0435 | .0366 | .0238 | .0361 | .061 | .0671 |
| Т0,ч | 57,5 | 60,8 | 34,3 | 148,5 | 23 | 27,3 | 41,9 | 27,7 | 16,4 | 14,9 |
| Варианты | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| λ | .0259 | .0459 | .028 | .0348 | .0203 | .0348 | .0102 | .0058 | .0416 | .027 |
| Т0,ч | 38,6 | 21,8 | 35,7 | 28,8 | 49,2 | 28,8 | 98,5 | 174 | 20,6 | 37 |