Функции алгебры логики

Дата: 2025-05-25; Просмотры: 3
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Применение структурно-логического метода будем рассматривать на примере простой системы (ПРИМЕР № 13).Рассмотрим логико-вероятностный метод анализа структурной схемы надежности, основанный на применении функции алгебры логики (ФАЛ).

Применение ФАЛ основано на том, что каждый элемент структурной схемы надежности может находиться лишь в двух состояниях: исправном (обозначается «1») и отказовом (обозначается «0»). ФАЛ – это логическая формула работоспособного/неработоспособного состояния.

Нормальной формой ФАЛ называют формулу, приведенную к виду, содержащему только операции сложения, умножения и отрицания. ФАЛ преобразуется в нормальную форму путем применения основных законов логики.

Применяются два метода составления ФАЛ:

1 – определение всех возможных минимальных условий по безотказности элементов, которые обеспечивают работоспособное состояние системы. Этот метод применяют для составления логических схем методами минимальных путей функционирования и минимальных сечений отказов (подробнее – позднее);

2 – рассмотрение всех возможных несовместных работоспособных состояний системы.

 

ПРИМЕР № 13

Проанализировать надежность системы, изображенной на рисунке. Составить логические формулы работоспособного и неработоспособного состояний. Найти выражение для вероятности безотказной работы системы при равнонадежных элементах. Составить дерево отказов.

 

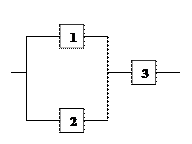
Составим ФАЛ работоспособного состояния с учетом совместных событий:

.

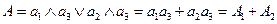Аналогично ФАЛ неработоспособного состояния:

.

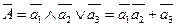Вероятность безотказной работы системы вычисляется на основе теорем сложения и умножения вероятностей:

.

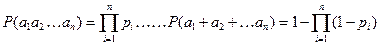В нашем случае, при независимости событий: P( A)=1-(1- pA1)(1- pA2)= pA1+ pA2- pA1 pA2=( pA1= p1 p3, pA2= p2 p3)= p1 p3+ p2 p3- p1 p2 p3= p3( p1+ p2- p1 p2). Здесь учтено также, что по правилам логики а i ai= ai.

При равной надежности элементов системы Р(А)=р2(2-р)=2р2-р3.

Дерево отказов выглядит следующим образом:

 

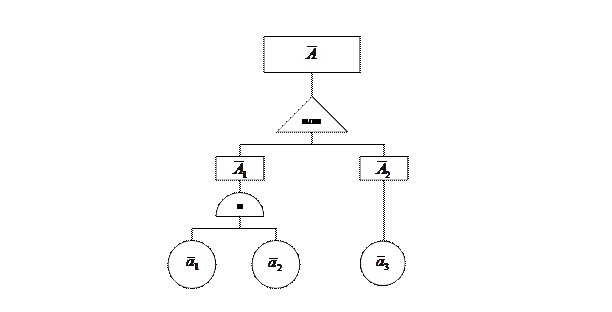
Проделаем то же самое, описав возможные работоспособные состояния системы с учетом несовместных событий (ФАЛ в такой форме называется совершенной дизъюнктивной нормальной формой – СДНФ):

 

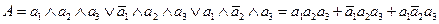
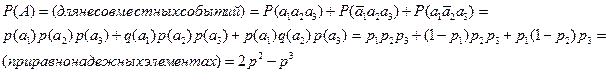
Таблица истинности для ФАЛ

 

В таблице истинности должны быть рассмотрены все возможные комбинации работоспособного и неработоспособного состояний элементов системы (табл.2.1). В системе, состоящей из n элементов, таких состояний может быть 2n.

Таблица 2.1

Таблица истинности ФАЛ

1 2 3 А ФАЛ состояния системы Вероятность состояния системы (при равнонадежных элементах)
0 0 0 0 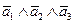q3=(1-p)3
0 0 1 0 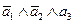q2p=p(1-p)2=p-2p2+p3
0 1 0 0 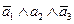q2p=p(1-p)2=p-2p2+p3
0 1 1 1 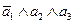qp2=p2(1-p)=p2-p3
1 0 0 0 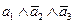q2p=p(1-p)2=p-2p2+p3
1 0 1 1 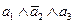qp2=p2(1-p)=p2-p3
1 1 0 0 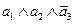qp2=p2(1-p)=p2-p3
1 1 1 1 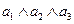p3

 

Суммируя все работоспособные состояния, получим: Р(А)=2р2-р3.

 

Мажоритарная система представляет собой вариант системы с параллельным соединением элементов, в которой отказ происходит при потере работоспособности не всех ее элементов, а какой-то их части. Обозначение такой системы «А из Б», где А и Б – числа, указывает на то, что отказ системы наступает, когда работоспособность сохраняют менее чем А любых ее элементов.

Для расчета надежности мажоритарных систем используют различные методы. При небольшом количестве элементов это может быть метод прямого перебора. Суть его заключается в следующем. Для каждой их возможных комбинаций состояний элементов системы по теореме умножения вычисляют ее вероятность. Если k-е состояние характеризуется тем, что из n элементов работоспособны k, а остальные нет, то вероятность такой комбинации равна

.

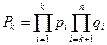Затем по теореме суммирования вероятностей складывают вероятности всех работоспособных состояний. Так определяют вероятность безотказной работы мажоритарной системы. При большом количестве элементов метод прямого перебора трудоёмок, поэтому применяют комбинаторный метод. Вероятность события, при котором из общего количества n элементов работоспособны k элементов, равна

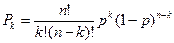. (2.8)

Вероятность безотказной работы системы с k≥m работоспособными элементами из общего их количества n равна

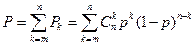, (2.9)

где биномиальный коэффициент из n элементов по k равен числу сочетаний из n по k:

.

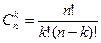Мажоритарная система при m=1 совпадает с системой параллельного соединения элементов, а при m=n – последовательного. Вероятность безотказной работы мажоритарной системы всегда выше, чем последовательной, и ниже, чем параллельной систем (табл. 2.2).

Таблица 2.2

Вероятность безотказной работы мажоритарной системы

m

n
1 2 3 4 5
1 p 2p-p2 3p-3p2+p3 4p-6p2+4p3-p4 5p-10p2+10p3-5p4+p5
2 - p2 3p2-2p3 6p2-8p3+3p4 10p2-20p3+15p4-4p5
3 - - p3 4p3-3p4 10p3-15p4+6p5
4 - - - p4 5p4-4p5
5 - - - - p5

 

В мостиковых системах параллельные ветви элементов соединены между собой другими элементами. В простых случаях расчет надежности мостиковой системы может быть проведен методом прямого перебора, но с учетом положения элементов в схеме.

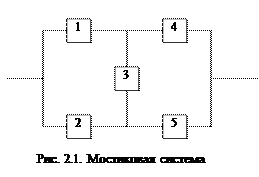
Если схема системы не сводится к одному из простых видов соединений, прибегают к логико-вероятностному методу ее анализа, в котором применяется аппарат математической логики. Логико-вероятностный анализ состоит в разработке формальной модели системы в виде соотношений алгебры логики, определяющей условия работоспособности/неработоспособности системы. Каждый i-й элемент может находиться в одном из несовместных событий: работоспособном a или неработоспособном 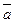состоянии. Рассмотрим пример простой мостиковой системы (рис. 2.1).

 

ЗАДАНИЕ К КОНТРОЛЬНОЙ РАБОТЕ 2

 

Проанализировать надежность системы, изображенной на рис. 2.2. Составить логические формулы работоспособного и неработоспособного состояний. Найти выражение для вероятности безотказной работы системы P(A) и ее значение по известным значениям вероятности безотказной работы элементов pi. Составить дерево отказов.

Рис. 2.2. Расчетная система

 

Варианты

Вариант 1 2 3 4 5 6 7 8 9 10
p1 0,7 0,7 0,7 0,7 0,7 0,6 0,6 0,6 0,9 0,8
p2 0,9 0,8 0,6 0,6 0,6 0,8 0,7 0,7 0,7 0,7
p3 0,7 0,9 0,8 0,9 0,6 0,9 0,9 0,8 0,7 0,8
Вариант 11 12 13 14 15 16 17 18 19 20
p1 0,7 0,6 0,7 0,6 0,9 0,8 0,9 0,8 0,9 0,8
p2 0,6 0,6 0,7 0,6 0,6 0,8 0,9 0,9 0,7 0,7
p3 0,7 0,6 0,7 0,7 0,7 0,6 0,6 0,6 0,6 0,6

 

Решение. Логическая формула работоспособного состояния

.

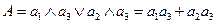Логическая формула неработоспособного состояния

.

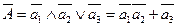Вероятность безотказной работы системы вычисляется на основе теорем сложения и умножения вероятностей:

.

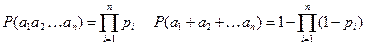В нашем случае P(A) =1 – (1 – pA1)(1 – pA2) = pA1 + pA2 - pA1pA2= (pA1=p1p3, pA2=p2p3) = p1p3+p2p3-p1p2p3=p3(p1+p2-p1p2). При равной надежности элементов системы Р(А)=р2(2–р).

Примечание: При переходе от логических формул к алгебраическим операциям умножения вероятностей следует учитывать, что aiai≡ ai.

 

ОТВЕТЫ

Варианты 1 2 3 4 5 6 7 8 9 10
Р(А) 0,68 0,85 0,70 0,79 0,53 0,83 0,78 0,70 0,68 0,75
Варианты 11 12 13 14 15 16 17 18 19 20
Р(А) 0,62 0,50 0,64 0,59 0,67 0,58 0,59 0,59 0,58 0,56