Уравнение Колмогорова для состояний. Предельные вероятности состояний
Практическое занятие 1
Уравнение Колмогорова для состояний. Предельные вероятности состояний
Рассмотрим систему, которая может находиться в 4-х состояниях: S0 – оба узла исправны; S1 – первый узел в ремонте; S2 – второй узел в ремонте; S3 – оба узла в ремонте (рис. 1).
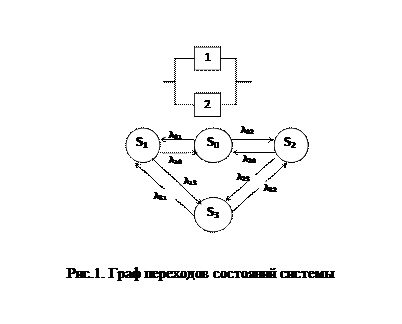
Вероятностью i-го состояния называется вероятность pi(t) того, что в момент t система будет находиться в состоянии Si. Очевидно, что для любого момента t сумма вероятностей всех состояний равна единице.
Рассмотрим систему в момент t и, задав малый промежуток Δt, найдем вероятность p0(t+Δt) того, что система в момент t+Δt будет находиться в состоянии S0. Это достигается разными способами.
1. Система в момент t с вероятностью p0(t) находилась в состоянии S0, а за время Δt не вышла из него.
Вывести систему из этого состояния можно суммарным простейшим потоком с интенсивностью (λ01+λ02), т.е. с вероятностью, приближенно равной (λ01+λ02)Δt. А вероятность того, что система не выйдет из состояния S0, равна [1-(λ01+λ02)Δt]. Вероятность того, что система будет находиться в состоянии S0 (т.е. того, что находилась в состоянии S0 и не выйдет из него за время Δt), по теореме умножения вероятностей равна:
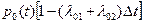
2. Система в момент t с вероятностями р1(t) (или p2(t)) находилась в состоянии S1 или S2 и за время Δt перешла в состояние S0.
Потоком интенсивностью λ10 (или λ20) система перейдет в состояние S0 с вероятностью, приближенно равной λ10Δt (или λ20Δt). Вероятность того, что система будет находиться в состоянии S0 по этому способу, равна р1(t)λ10Δt (или р2(t)λ20Δt).
Применяя теорему сложения вероятностей, получим
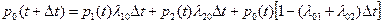 ,
,
oткуда
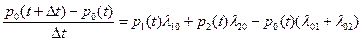 .
.
Переходя к пределу при Δt=0 получим в левой части уравнения производную dp0(t)/dt:
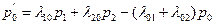 .
.
Рассуждая аналогично для других состояний системы Si, можно получить систему дифференциальных уравнений Колмогорова для вероятностей состояний:
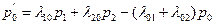 ,
,
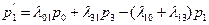 ,
,
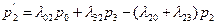 ,
,
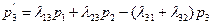 .
.
Сформулируем правило составления уравнений Колмогорова. В левой части каждого из них стоит производная вероятности i-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).
В системе независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение:
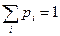
Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент t = 0. Так, например, рассматриваемую систему уравнений естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии S0, т.е. при начальных условиях p0(0)=1, p1(0)=p2(0)=p3(0)=0.
Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени. Особый интерес представляют вероятности системы pi(t) в предельном стационарном режиме, т.е. при t=∞, которые называются предельными (или финальными) вероятностями состояний.
В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.
Предельная вероятность состояния Si имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии. Например, если предельная вероятность состояния S0 p0=0,5, то это означает, что в среднем половину времени система находится в состоянии S0.
Так как предельные вероятности постоянны (не зависят от времени), то заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для нашего случая такая система уравнений имеет вид:
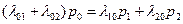 ,
,
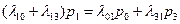 ,
,
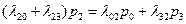 ,
,
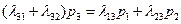 .
.
Эту систему можно составить непосредственно по размеченному графу состояний, если руководствоваться правилом, согласно которому слева в уравнениях стоит предельная вероятность данного состояния pi, умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.
ПРИМЕР. Найти предельные вероятности для рассмотренной выше системы S при λ01=1, λ02=2, λ10=2, λ13=2, λ20=3, λ23=1, λ31=3, λ32=2.
Решение. Система алгебраических уравнений, описывающих стационарный режим данной системы, имеет вид:
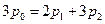 ,
,
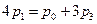 ,
,
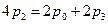 ,
,
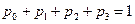 .
.
ПРИМЕЧАНИЕ: Здесь вместо одного «лишнего» уравнения системы мы записали условие нормировки.
Решив систему, получим: p0=0,40, p1=0,20, p2=0,27, p3=0,13, т.е. в предельном, стационарном режиме система S в среднем 40% времени будет находиться в состоянии S0 (оба узла исправны), 20% — в состоянии S1 (первый узел ремонтируется, второй работает), 27% — в состоянии S2 (второй узел ремонтируется, первый работает) и 13% времени — в состоянии S3 (оба узла ремонтируются).
ЗАДАНИЕ К КОНТРОЛЬНОЙ РАБОТЕ 1
Техническое устройство может находиться в одном из трех состояний S0, S1, S2. Интенсивность потоков, которые переводят устройства из одного состояния в другое, известны (варианты в таблице).
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| λ01 | 3 | 1 | 3 | 0 | 5 | 4 | 1 | 1 | 3 | 1 |
| λ02 | 5 | 2 | 2 | 1 | 0 | 2 | 3 | 3 | 4 | 2 |
| l10 | 1 | 3 | 5 | 2 | 3 | 1 | 5 | 0 | 5 | 1 |
| l12 | 2 | 5 | 4 | 5 | 4 | 0 | 2 | 5 | 2 | 4 |
| l20 | 0 | 4 | 1 | 4 | 2 | 3 | 0 | 2 | 1 | 1 |
| l21 | 4 | 0 | 0 | 3 | 1 | 5 | 4 | 2 | 3 | 2 |
| Вариант | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| λ01 | 2 | 2 | 5 | 2 | 3 | 3 | 4 | 0 | 4 | 1 |
| λ02 | 0 | 1 | 1 | 3 | 2 | 3 | 4 | 1 | 0 | 2 |
| l10 | 3 | 4 | 3 | 2 | 4 | 0 | 5 | 5 | 4 | 5 |
| l12 | 5 | 1 | 2 | 3 | 5 | 2 | 3 | 1 | 1 | 3 |
| l20 | 2 | 4 | 1 | 0 | 1 | 5 | 2 | 2 | 2 | 4 |
| l21 | 1 | 2 | 4 | 1 | 0 | 1 | 1 | 3 | 5 | 2 |
Необходимо построить размеченный граф состояний, записать систему уравнений Колмогорова, найти финальные вероятности и сделать анализ полученных решений.
Пример решения: Техническое устройство может находиться в одном из трех состояний S0, S1, S2. (рис. 2).
 |
Интенсивность потоков, переводящих устройство из состояния, заданы в таблице.
| λ01 | λ02 | λ10 | λ12 | λ20 | λ21 |
| 2 | 2 | 1 | 2 | 3 | 0 |
По графу запишем систему уравнений Колмогорова в общем виде:
dp 0 ( t )/ dt =λ10 p 1 ( t )+λ20 p 2 ( t )-(λ01+λ02) p 0 ( t );
dp 1 ( t )/ dt =λ01 p 0 ( t )+λ21 p 2 ( t )-(λ10+λ12) p 1 ( t );
dp 2 ( t )/ dt =λ02 p 0 ( t )+λ12 p 1 ( t )-(λ20+λ21) p 2 ( t );
p0(t)+p1(t)+p2(t)=1.
Вместо интенсивности потоков λij запишем их значения и получим систему:
dp0(t)/dt=p1(t)+3p2(t)-4p0(t);
dp1(t)/dt=2p0(t)-3p1(t);
dp2(t)/dt=2p0(t)+2p1(t)-3p2(t);
p 0 ( t )+ p 1 ( t )+ p 2 ( t )=1.
Чтобы найти финальные вероятности состояний, в уравнениях Колмогорова отбросим первое уравнения, а по остальным составим систему алгебраических уравнений:
2p0-3p1=0;
2p0+2p1-3p2=0;
p0+p1+p2=1.
Результат: При достаточно большом времени работы техническое устройство с вероятностью p0=0,36 будет находиться в состоянии S0, с вероятностью p1=0,24 в состоянии S1 и с вероятностью p2=0,4 в состоянии S2.
Правильность расчетов проверяется по условию нормировки: 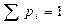 .
.








