Рассмотрим третью задачу анализа модели на чувствительность. В каких пределах допустимо изменение коэффициентов целевой функции?
В рамках анализа модели задачи на чувствительность к изменениям коэффициентов целевой функции могут исследоваться следующие вопросы:
1) каков диапазон изменения (увеличения или уменьшения) того или иного коэффициента целевой функции, при котором не происходит изменения оптимального решения?
2) насколько следует изменить тот или иной коэффициент целевой функции, чтобы сделать некоторый недефицитный ресурс дефицитным и, наоборот, дефицитный ресурс сделать недефицитным?
Рассматривая первый вопрос, обозначим через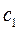 
и 
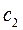доходы фабрики от продажи 1 т краски К1 и 1 т краски К2 соответственно. Тогда целевую функцию можно представить в следующем виде: 
.
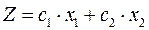Переместим линию уровня вправо параллельно самой себе до совмещения с точкой максимума С. При увеличении 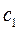или уменьшении 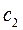линия уровня вращается (вокруг точки С) по часовой стрелке.
Если же 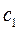уменьшается или 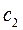увеличивается, эта прямая вращается в противоположном направлении - против часовой стрелки. Таким образом, точка С будет оставаться оптимальной точкой до тех пор, пока наклон прямой не выйдет за пределы, определяемые наклонами прямых, соответствующих ограничениям (1) и (2). Когда наклон линии уровня станет равным наклону прямой (1), получим две альтернативные оптимальные угловые точки С и D. Аналогично, если наклон линии уровня станет равным наклону прямой (2), будем иметь альтернативные оптимальные угловые точки В и С. (Наличие альтернативных оптимумов свидетельствует о том, что одно и то же оптимальное значение 
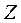может достигаться при различных значениях переменных. Как только наклон линии уровня выйдет за пределы указанного выше интервала, получим некоторое новое оптимальное решение (точка В или точка D).
Найдем допустимый интервал изменения 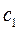, при котором точка С остается оптимальной. Исходное значение коэффициента 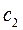= 2 оставим неизменным, а значение 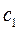можно увеличивать до тех пор, пока линия уровня не совпадет с прямой (2), или уменьшать, пока линия уровня не совпадет с прямой (1). Эти крайние значения коэффициента 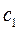можно определить из равенства наклонов линии уровня и прямой (2) (максимальное значение линии уровня) и равенства наклонов линии уровня и прямой (1) (минимальное значение ).
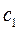Найдем угловой коэффициент линии уровня: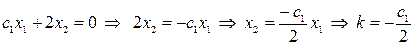 
, угловой коэффициент граничной прямой (1): 
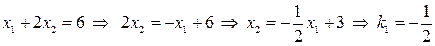, и угловой коэффициент граничной прямой (2): 
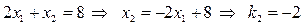. Из равенства 
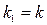, или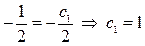 
находим минимальное значение 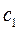, а из равенства 
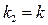, или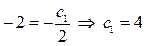 
- максимальное значение 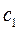. Таким образом, 
, 
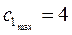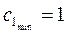, то есть оптимальное решение задачи не изменится, если оптовая цена краски К1 будет находиться в диапазоне от 1 до 4 тыс. долл., при этом доход фабрики будет заключен в пределах от 6 до 16, тыс. долл. ( 
, 
).
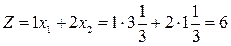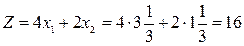Аналогично находится диапазон изменения коэффициента 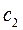если 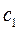будет неизменным: 
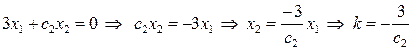- угловой коэффициент линии уровня. Из равенства 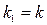, или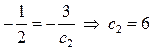 
находим максимальное минимальное значение 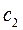, а из равенства 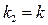, или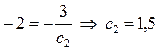 
- минимальное значение 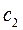. Таким образом, 
, 
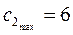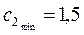, то есть оптимальное решение задачи не изменится, если оптовая цена краски К2 будет находиться в диапазоне от 1,5 до 6 тыс. долл., при этом доход фабрики будет заключен в пределах от 12 до 18, тыс. долл. ( 
, 
).
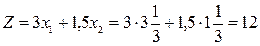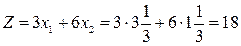Таким образом, из приведенных выше расчетов и графической их иллюстрации следует, что если цена на краску первого вида станет меньше 1 тыс. руб./т (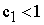 
), то наиболее выгодным будет производство красок в точке D (см. рисунок). При этом общее потребление сырья В снизится, что приведет к его недефицитности (прямая (2)), а дефицитными будут ресурсы (1) и (4).