§9.4. алгоритмы, обеспечивающие функционирование аналитических и цифровых фотограмметрических систем
Ниже приведены алгоритмы, обеспечивающие функционирование аналитических фотограмметрических систем (аФС). Для цифровых фотограмметрических систем эти алгоритмы аналогичны, за исключе- нием калибровки измерительных систем стереокомпаратора, который отсутствует в цифровых системах. в качестве измерительной системы в цифровых фотограмметрических системах выступает сами цифровые изображения, подлежащие обработке. Кроме того отличительной осо- бенностью алгоритмов, обеспечивающих функционирование цифровых фотограмметрических систем, является большая степень автоматизации
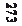 Т а б л и ц а 9.1
Т а б л и ц а 9.1
|
Фотограмметри- ческая система |
Год появления на рынке |
Типы изображений |
Стереонаблюдения | Фотометриче- ская обработка | Фототриангуляция | ЦМП, ЦМР, Ортофотоплан | Создание контур- ной части карты | |||||||||||||||
| Изменение контраста | Методы интерполирования яркостей | Фотометрическая коррекция | внутреннее ориентирование | взаимное ориентирование | внешнее ориентирование | Отбраковка грубых измерений | Самокалибровка | выделение линий перегиба | Редактирование ЦМР | Создание плотной ЦМП | Создание ЦМР по ЦМП | Проведение линии пореза с учетом контуров | Создание фотоплана | Создание действительного ортофото | выделение контурных точек | выделение линейных объектов | выделение зданий | Наложение на модель 3D-векторов | ||||
| Фотомод | 1994 | 0,2,3,4 | а,З,П | 7 | С,Б,К | 7 | 7 | 7 | 5 | 7 | 7 | 5,6 | 5 | 7 | + | 5 | 7 | – | 6 | 6 | 6 | + |
| ЦФС ЦНИИГаиК/ DIGITALS ГЕО- СИСТЕМа | 1995 | 0,1,2,4 | Б,П, а,З | 7 | С,Б,К | 7 | 7 | 7 | 5 | 7 | 7 | 5,6 | 5 | 7 | + | 6 | 7 | 6 | 6 | 6 | 6 | + |
| Фотоскан | 2006 | 0,4 | – | 7 | С,Б,К | 7 | 7 | 7 | 5 | 7 | 7 | – | – | 7 | – | 7 | 7 | 7 | – | – | – | – |
| INPHO | 1980 | 0,2,3,4 | а,З,П | 7 | С,Б,К | 7 | 7 | 7 | 5 | 7 | 7 | 5,6 | 5 | 7 | + | 7 | 7 | – | 6 | 6 | 6 | + |
| IMAGINE Photogrammetry | 1991 | 0,2,3,4 | а,З | 7 | С,Б,К | 7 | 7 | 7 | 5 | 7 | 7 | 5,6 | 5 | 7 | + | 7 | 7 | 7 | – | 6 | 6 | + |
| Correlator3D | 2003 | 0,2,3,4 | – | 7 | С,Б,К | 7 | 7 | 7 | 5 | 7 | 7 | 7 | 5 | 7 | + | 7 | 7 | 7 | 6 | 6 | 6 | + |
| SURE | 2013 | 0,2,4 | – | 7 | С,Б,К | 7 | – | – | – | 7 | – | – | – | 7 | – | – | 7 | 7 | – | – | – | – |
| Pix4Dmapper | 2014 | 0,4 | – | 7 | С,Б,К | 7 | 7 | 7 | 5 | 7 | 7 | 7 | 5 | 7 | + | 7 | 7 | 7 | 6 | 6 | 6 | + |
Обозначения: 0 — кадровые снимки; 1 — панорамные снимки; 2 — сканерные изображения; 3 — радиолокационные изображения; 4 — снимки, полученные с БПла; 5 — интерактивный; 6 — автоматизированный; 7 — автоматический; Б — бинокулярная оптическая насадка; П — поляроидный метод наблюдения; а — анаглифический метод наблюдения; З — затворные очки; С — метод «ближайшего соседа»; Б — билинейный метод интерполирования яркостей; К — кубический метод интерполирования яркостей
измерений точек снимков на всех этапах их обработки. вопросы авто- матизации измерений были рассмотрены отдельно в главе 5.
калибровка измерительных систем стереокомпаратора аналитических фотограмметрических систем
Производится с помощью специальной измерительной сетки, пред- ставляющей собой плоскопараллельную стеклянную пластину, на одной из поверхностей которой нанесена сетка крестов, координаты которых известны с высокой точностью (до 0,5 мкм) (рис. 9.3).
Измерительную сетку закладывают в каретку стереокомпаратора и измеряют координаты крестов в системе координат (СК) измерительной системы Ocxcyc. Для исключения систематических ошибок измеритель- ных систем обычно используют формулы аффинных преобразований:
æ x k ö = æ a0 ö + Ïæ xc ö = æ a0 ö + æ a1
a2 öæ xc ö
(9.4.1)
ç y ÷ ç b
÷ ç y ÷ ç b ÷
ç b b
÷ç b ÷
или
è k ø è
0 ø è
c ø è 0 ø
è 1 2 øè c ø
x k = a0 + a1xc + a2yc;
y = b
+ b x
+ b y , (9.4.2)
k 0 1 c 2 c
где xc, yc — координаты точки в системе координат измерительной си- стемы; x k, y k — координаты точки в системе координат измерительной сетки (истинные значения координат, которые мы в дальнейшем будем называть координатами в системе координат калибровочной изме-
 |  | ||
рис. 9.3
рительной системы); a i, b i — параметры аффинного преобразования;
П — матрица аффинного преобразования.
Параметры a0, b0 являются координатами начала СК измерительной сетки в СК измерительной системы, а посредством параметров a1, a2, b1,b2 учитывают неперпендикулярность осей СК измерительной системы и отличие масштабов датчиков координат от номинальных значений.
Каждый измеренный крест измерительной сетки позволяет соста- вить два уравнения поправок:
a0 + a1xc + a2yc - x k = v x ;
b + b x
+ b y - y
= v . (9.4.3)
0 1 c 2 c k y
Очевидно, что для определение шести параметров аффинного пре- образования необходимо измерить не менее трех крестов не лежащих на одной прямой. Обычно при калибровке измеряют 25 крестов, равно- мерно расположенных на измерительной сетке. Определение параметров аффинного преобразования производят в результате решения системы уравнений поправок (9.4.3) по методу наименьших квадратов.
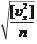
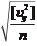 По значениям поправок v x, v y определяют средние квадратические ошибки измерения координат х и ó (точность измерительных систем стереокомпаратора):
По значениям поправок v x, v y определяют средние квадратические ошибки измерения координат х и ó (точность измерительных систем стереокомпаратора):
m x =
; m y = ,
(9.4.4)
где n — количество измеренных крестов.
При последующей фотограмметрической обработке снимков вы- числение координат точек снимка в СК калиброванной измерительной системы производят по формулам
æ x k ö = Ïæ xc ö
(9.4.5)
ç y ÷ ç y ÷
или
è k ø è c ø
x k = a1xc + a2yc;
y k = b1xc + b1yc. (9.4.6)
При обработки снимков на аналитической фотограмметрической системе возникает задача определения координат точек в СК изме- рительной системы по значениям их координат в СК калиброванной измерительной системы. Эти определения производят по формулам:
æ xc ö = Ï-1 æ x k ö
(9.4.7)
ç y ÷ ç y ÷
или
è c ø è k ø
xc = A1x k + A2y k ;
y = B x + B y , (9.4.8)
c 1 k 2 k
|
в которых A i, B i — элементы обратной матрицы П .
Внутреннее ориентирование снимков
Для фотограмметрической обработки снимка необходимо измерить координаты точек снимка х, ó в СК снимка ох ó. При наведении измери-
тельной марки на точку снимка
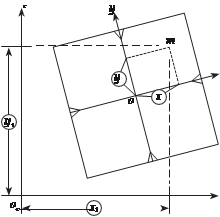 y датчики координат измеритель-
y датчики координат измеритель-
ной системы стереокомпаратора
фиксируют координаты точки
х , ó в СК измерительной систе-
c c
x мы оcхcóc (рис. 9.4).
Зная параметры калибровки
a , b , вычисляют координаты
i i
точки в СК калиброванной си- стемы:
x k = a1xc + a2yc;
y = bx + b y . (9.4.9)
k 1 c 2 c
рис. 9.4
xc Для определения коорди- нат точек х, ó в СК снимка по координатам этих точек, опре- делённых в СК калиброванной
измерительной системы х k, ó k, обычно используют формулы аффинного преобразования:
æ x ö = æ a o¢ ö + P æ x k ö = æ a o¢ ö + æ a1¢
a2¢ öæ x k ö
(9.4.10)
ç y ÷
ç b¢ ÷
ç y ÷
ç b¢ ÷
ç b¢
b¢ ÷ç y ÷
или
è ø è o ø
è k ø
è o ø
è 1 2 øè k ø
x = a o¢ + a1¢x k + a2¢y k ; y = b o¢ + b1¢x k + b2¢y k .
Параметры аффинного преобразования a i¢, b i¢ позволяют учесть не только положение и ориентацию СК снимка в СК калиброванной из- мерительной системы, но и учесть систематические искажения снимка,
вызываемые изменением масштабов снимка по осям х, ó и неперпенди- кулярностью осей х и ó. Эти искажения возникают из-за деформации фотоплёнки, на которой был получен снимок.
Параметры a i¢, b i¢ можно определить по координатам х k, ó k коорди- натных меток, полученным в результате их измерения на аналитической
стереофотограмметрической системе (аСФС), и значениям координат этих меток х, ó, полученным при калибровке съёмочной камеры.
Для определения параметров a i¢, b i¢ для каждой координатной метки составляют уравнения
a o¢ + a1¢x k + a2¢y k - x = V x ;
b o¢ + b1¢x k + b2¢y k - x = V y
(9.4.11)
и решают полученную систему уравнений по методу наименьших квадратов.
Очевидно, что для определения параметров a i¢, b i¢ необходимо из- мерить координаты не менее трех меток, не лежащих на одной прямой.
При обработке снимков на аСФС возникает задача определения координат точек снимка в СК калиброванной измерительной системы по их значениям в СК снимка. Определения производят по формулам
æ x k ö = P-1 æ x - a o¢ ö = æ A1¢
A2¢ öæ x - a o¢ ö
(9.4.12)
ç k ÷ ç y - b o¢ ÷ ç B1¢
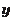
B2¢ ÷ç y - b o¢ ÷
или
è ø è ø è
øè ø
где
x k = A1¢(x - a o¢ ) + A o¢ (y - b o¢ );
y k = B1¢(y - y o¢ ) + B2¢ (y - b o¢ ),
A i¢, B i¢ — элементы обратной матрицы P‒1.
(9.4.13)
в случае, если при калибровке съёмочной камеры определялись калиброванные расстояния между координатными метками l x, l y для определения координат точек в СК снимка по измеренным координатам
точек в системе калиброванной измерительной системы используют формулы
x = k x[cos j(x k - a o ) + sin j(y k - b o )];
y = k y[-sin j(x k - a o ) + cos j(y k - b o )],
(9.4.14)
в которых a o, b o — координаты начала СК снимка в СК калиброванной измерительной системы; j — угол разворота СК снимка относительно СК калиброванной системы; k x, k y — коэффициенты деформации снимка по осям х и ó.
Если калиброванные расстояния между координатными метками l x, l y неизвестны (рис. 9.5), то для определения координат точек в системе координат снимка используют формулы:
x = cos j(x k - a o ) + sin j(y k - b o );
y = -sin j(x
- a ) + cosj(y
- b ).
(9.4.15)
yc y
3
|
l x
y
o φ
k o k o
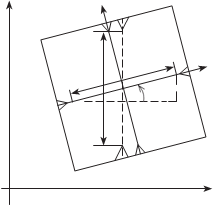 Значение параметров j, a o, b o, k x, k y определяют по измерен- ным значениям координат коор-
Значение параметров j, a o, b o, k x, k y определяют по измерен- ным значениям координат коор-
x динатных меток в СК калибро- ванной измерительной системы
2 по формулам:
1
j= arctg
4
y - y

|
|
2 1
|
|
-
2 1
(9.4.16)
|
где x k , y k , x k , y k — координаты
oc
рис. 9.5
xc 1 и 2 координатных меток в СК калиброванной измерительной системы;

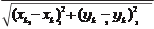 k = l x = l x ;
k = l x = l x ;
x l
xj
l y l y

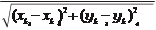 k y = l =
k y = l =
(9.4.17)
;
yj
где l x, l y — калиброванные значения расстояний между координатными
|
метками; x k , y k — координаты координатных меток в СК калиброван-
ной измерительной системы.
Параметры a o, b o определяют, как координаты x k, y k точки пере- сечения прямых линий, проведённых через координатные метки 1–2 и 3–4, по формулам:
a = (y k
- y k ) + a1x k
- a2 x k ;

|
o a - a
1 2
b o = y k + a1(a o - x k ) = y k + a2 (a o - x k ),
(9.4.18)
1 1 4 4
где a
= y k2 - y k1 ; b = y k3 - y k4 .


|
|
|
|
|
|
x k - x k x k - x k
Для определения координат точек снимка в СК калиброванной измерительной системы по координатам этих точек в СК снимка ис- пользуют формулы:
если калиброванные расстояния l x, l y между координатными мет- ками известны
x = a + 1 (x cosj - y sin j);
|
k o
x
(9.4.19)
y = b + 1 (x sin j + y cos j);
|
k o
x
если калиброванные расстояния не известны
x k = a o + x cos j - y sin j;
y = b + x sin j + y cosj.
(9.4.20)
k o








