§8.3. объединение и внешнее ориентирование отдельных дискретных моделей в общую модель объекта
 Z'
Z'
S4
 Z' Y'
Z' Y'
X'
S1
Объект
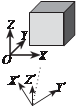 S2
S2
На практике, для получения
 Z ' трехмерной модели всего объекта
Z ' трехмерной модели всего объекта
Y ' бывает недостаточно снять его
X ' S3 с одной точки, поэтому делают серию съемок с различных то-
чек стояния S i (рис. 8.11). в этом случае возникает задача объ- единения трехмерных моделей
рис. 8.11
объекта в единую модель. Эта задача решается по связующим
точкам, которые располагаются в зоне перекрытия между моделями. в качестве связующих точек часто используют специальные отражатели- маркеры (те же, что и для внешнего ориентирования модели), которые легко опознаются в соседних моделях.
Задача объединения моделей решается на основе уравнений (8.2.1) аналогично внешнему ориентированию модели. Далее общая модель ориентируется внешне по опорным точкам по методу, описанному в §8.2. в результате имеем X, Y, Z, d для всей совокупности точек объекта в единой системе координат объекта OXYZ.
Иногда в качестве связующих точек используют естественные контуры объекта, попавшие в зону перекрытия моделей. Измерение связующих точек может выполняться в интерактивном режиме с по- мощью оператора или автоматически.
На рис. 8.12 показан пример объединения (взаимного ориенти- рования) двух моделей, по связующим точкам, измерение которых выполнялось автоматически (рис. 8.12, а — две исходные модели, рис. 8.12, б — общая модель объекта).

а б
рис. 8.12
§8.4. визуализация трехмерных дискретных моделей
Как отмечалось выше, для каждой точки модели объекта фиксиру- ется интенсивность отраженного сигнала, которая может быть исполь- зована для визуализации объекта в так называемых псевдоцветах. Для получения реальных яркостей в каждой точке сканирования в сканере применяется цифровая камера, основанная на матрице ПЗС (рис. 8.13). С помощью этой камеры сначала получают серию изображений, по- крывающих весь объект в пределах предполагаемого сканирования. Затем объект сканируют, а соответствующие яркости берут с этих снимков. Такой подход позволяет в последующей обработке оперировать не только с облаком точек лазерного сканирования, но и с цифровыми изображениями объекта, что существенно повышает информативность полученной информации об объекте.
|
Рассмотрим более подробно получение яркостей изображе- ния для каждой точки сканиро- вания со снимков. Итак, сначала производится съемка всего объ- екта путем поворотов и наклонов камеры (или соответствующего зеркала) с помощью моторов последовательно на углы, рав- ные углам поля зрения камеры
(см. рис. 8.13). Здесь стрелками
рис. 8.13
 y
y
z S i
x Объект
f
|
r→ m
показаны возможные повороты и наклоны камеры в системе координат сканера.
|
Z' R
S
R M
Si →
Y' R M
φ v
X'
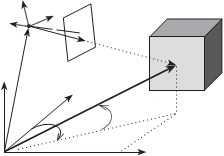
На рис. 8.14 показаны систе- ма координат сканера SX′Y′Z′, в которой производится определе- ние координат точек объекта М, и система координат камеры S ix yz, которая может изменять свое
положение и ориентацию от- носительно системы координат
рис. 8.14
сканера во время съемки. Наша
задача найти координаты вектора r в системе координат камеры с тем, чтобы по ним взять со снимка в точке m соответствующую яркость d изображения точки M объекта.
Из рис. 8.14 следует, что
или
|
R R M
NA r =
|
R Si
-
(8.4.1)
, (8.4.2)
i R M R Si
где N — скаляр; аi — матрица поворота системы координат камеры в момент съемки i относительно система координат сканера; r — век- тор, определяющий положение точки m в системе координат камеры;
R M — вектор, определяющий положение точки M в системе коорди-
нат сканера; R Si — вектор, определяющий положение начала системы
координат камеры относительно системы координат сканера в момент съемки i.
Из (8.4.2) имеем
r = AT 1 ( - ) (8.4.3)
i N R M R Si
или в координатной форме
æ x ö
1 æ X ¢ - X Si ö
ç y ÷ = AT
ç Y ¢ - Y ÷. (8.4.4)
ç ÷ i N ç
Si ÷
ç -f ÷
ç Z ¢ - Z Si ÷
è ø è ø
Если выразить из третьего уравнения выражения (8.4.4) значение 1/N и подставить в первые два, то получим известные в фотограмметрии уравнения коллинеарности:
 x = -f a11 ( X ¢ - X Si ) + a21 (Y ¢ - Y Si ) + a31 (Z ¢ - Z Si ) ;
x = -f a11 ( X ¢ - X Si ) + a21 (Y ¢ - Y Si ) + a31 (Z ¢ - Z Si ) ;
a13 ( X ¢ - X Si ) + a23 (Y ¢ - Y S Si ) + a33 (Z ¢ - Z Si )
a ( X ¢ - X ) + a (Y ¢ - Y ) + a (Z ¢ - Z )
(8.4.5)
y = -f 12
Si 22
Si 32
Si .
a113 ( X ¢ - X Si ) + a23 (Y ¢ - Y Si ) + a33 (Z ¢ - Z Si )
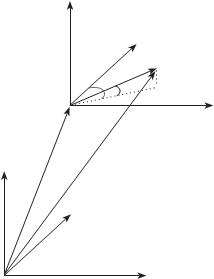
в этих уравнениях известны все величины, необходимые для вычисления координат x, y. Так, координаты точки объекта X′,Y′,Z′ вычисляются по (8.1.1), а элемен- ты внешнего ориентирования
снимка следующим образом. Как
Z'
 Y'
Y'
S i
c i
φk v k
следует из рис. 8.15, вектор
R Si ,
S o X'
определяющий положение цен- тра проекции камеры S i в момент
фотографирования i в системе Z '
координат сканера SX′Y′Z′, равен
R So
R Si
R Si
|
R S 0
+ c i , (8.4.6) Y '
где
R S 0 — вектор, определяю-
щий положение точки вращения камеры в системе координат сканера; c i — вектор, задающий
S X'
рис. 8.15
положение центра проекции камеры S i в системе координат S0X′Y′Z′, параллельной системе координат сканера SX′Y′Z′.
в координатной форме уравнение (8.4.6) имеет вид:
æ X Si ö æ X S 0 ö æ cos nk sin jk ö
ç Y Si ÷ = ç Y S 0 ÷ + c ç cos nk cosjk ÷,
(8.4.7)
ç ÷ ç ÷ ç ÷
ç Z Si ÷
ç Z S 0 ÷
ç sin jk ÷
è ø è ø è ø
где с — модуль вектора c i (величина постоянная для данного сканера и камеры); jk, νk — горизонтальный и вертикальный углы наклона камеры
(задаются и измеряются сканером — величины кратные соответствую- щим углам поля зрения камеры).
величины X S0, Y S0, Z S0, c являются постоянными для данного сканера и определяются в результате его калибровки. Направляющие косинусы a ij в (8.4.5) вычисляют по известным формулам, подставляя в них вместо α, ω соответствующие значения jk, νk, при этом κ = 0. в результате для каждой точки объекта с координатами X′,Y′,Z′ полу- чается яркость изображения d, взятая со снимка по координатам x, y,
вычисленным по (8.4.5).
Теперь трехмерную модель можно визуализировать в естествен- ных или псевдоцветах (рис. 8.16, 8.17) под различными углами зрения с целью ее измерения (векторизации элементов объекта, определения объемов, площадей и т.д.). Кроме того модель можно представить в виде триангуляции Делоне (см. рис. 8.16).
 |  |
рис. 8.16 рис. 8.17
§8.5. Подвижные сканерные системы
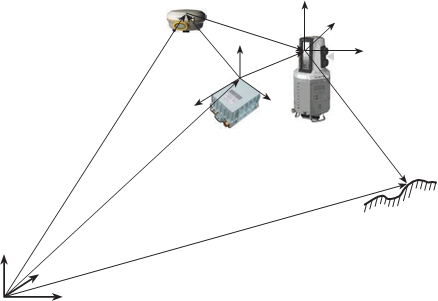
Подвижные сканерные системы предназначены для съемки протяжен- ных объектов, таких как улицы городов, тоннели, береговая линия и т.п. На рис. 8.18 показаны некоторые примеры подвижных сканерных систем. Подвижная сканерная система состоит из одного или нескольких сканеров, ГНСС-приемника и инерциальной геодезической системы INS.
все эти элементы жестко закре- плены на платформе, которая устанавливается на носитель (ав- томобиль, катер и др.). Очевидно, что во время сканирования по- ложение и ориентация самого сканера (системы координат сканера SX′Y′Z′) будут непрерыв- но изменяться из-за движения носителя, т.е. в каждый момент времени у сканера будут свои элементы внешнего ориентиро- вания. Для определения этих эле- ментов и служат GPS-приемник (определяет линейные элементы внешнего ориентирования ска-
нера X S,Y S,Z S) и инерциальная система INS (определяет угловые элементы внешнего ориентиро-
вания сканера α, ω, κ и линейные совместно с GPS), входящие в комплект подвижной сканерной системы. Кроме того, для точно- го определения координат точек объекта в системе координат объекта необходимо знать вза- имное положение всех элементов системы (GPS, INS и сканера), ко- торое определяется в результате калибровки системы.
Получим формулы для вы- числения координат точек объ- екта по результатам съемки с

рис. 8.18
помощью подвижной сканерной системы. На рис. 8.19:
OGPSXYZ — система координат объекта, в которой измеряется по- ложение антенны GPS (вектор RGPS );
SX′Y′Z′ — система координат сканера, в которой определяется по- ложение точки объекта М (вектор R );
GPS
|
→
GPS/INS
→
|
GPS/S
Z
→r
Z'
 Y'
Y'
S
X'
INS/S
X
|
RGPS
OINS
Y
→
R
→
RINS M
→
R M
Z
Y
OGPS X
рис. 8.19
OINSXYZ — система координат инерциальной навигационной си- стемы;
r , r , r — векторы, задающие взаимное положение инер-
INS/GPS INS/S GPS/S
циальной системы, сканера и антенны GPS.
|
Таким образом, вектор , определяющий положение точки М
объекта в системе координат объекта, можно получить по следующей формуле:
=
+ A r
+ A A
, (8.5.1)
где =
R M
- A r
RINS INS INS/S
.
INS INS/S R
RINS
RGPS INS GPS/INS
Тогда R M = RGPS + AINS[rINS/S - rGPS/INS + AINS/S R].
Окончательно получим
= + A [r + A ]. (8.5.2)
R M RGPS INS GPS/S INS/S R
в координатной форме уравнение (8.5.2) можно записать так:
æ X ö æ X GPS ö
éæ X GPS ö
æ X ¢öù
ç ÷ ç ÷
êç S ÷
ç ÷ú
|
ç Y ÷ = ç YGPS ÷ + AINS êç Y GPS ÷ + AINS/S ç Y ¢ ÷ú , (8.5.3)
ç Z ÷ ç ZGPS ÷
êç Z GPS ÷
ç Z ¢ ÷ú
è ø è ø
ëè S ø
è øû
где XGPSYGPSZGPS — координаты центра антенны GPS-приемника, которые измеряются с помощью этого приемника; AINS — матрица поворота, которая вычисляется по трем углам α, ω, κ, измеряемым инерциаль- ной системой, т.е. эта матрица определяет угловую ориентацию си- стемы координат OINSXYZ относительно системы координат объекта OGPSXYZ; AINS/S — матрица поворота, определяющая взаимную угловую ориентацию (углы ∆α, ∆ω, ∆κ) системы координат сканера SX′Y′Z′ и
системы координат инерциальной навигационной системы OINSXYZ;
X GPS , Y GPS, Z GPS — координаты вектора r , определяющего взаимное
S S S
GPS/S
положение сканера и антенны GPS в системе координат инерциальной системы; X′, Y′, Z′ — измеренные координаты точки объекта в системе координат сканера.
|
в уравнениях (8.5.3) величины X GPS , Y GPS, Z GPS и AINS/S — посто-
|
янные для данной подвижной сканерной системы и определяются в ре- зультате калибровки системы. Калибровка выполняется по тест-объекту, который представляет собой набор маркированных точек с известными координатами в системе координат объекта. Этот тест-объект скани- руется при неподвижном положении сканерной системы. в результате имеем координаты X′, Y′, Z′ всех точек тест-объекта. Кроме того, фикси- руются XGPSYGPSZGPS и α, ω, κ, при которых выполнялось сканирование. Таким образом, в уравнениях (8.5.3) неизвестны шесть параметров: X GPS , Y GPS, Z GPS , ∆α, ∆ω, ∆κ. Одна опорная точка дает три уравнения с шестью неизвестными, поэтому минимальное число опорных точек равно двум, однако, в этом случае может возникнуть неопределенность при вычислении угловых элементов. Поэтому минимальным числом опорных точек следует считать три точки, не лежащие на одной прямой. лучше иметь больше опорных точек, разнесенных по площади. Задача решается по методу наименьших квадратов при использовании всех
точек тест-объекта. в результате имеем неизвестные параметры, кото- рые используются при реальной съемке объекта. На рис. 8.20 показаны примеры съемок, выполненных подвижной сканерной системой.
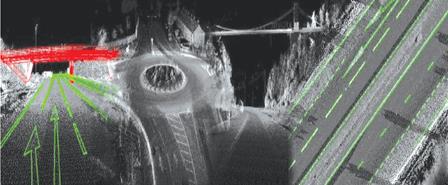
рис. 8.20
§8.6. Устройство и технические характеристики наземных лазерных сканеров
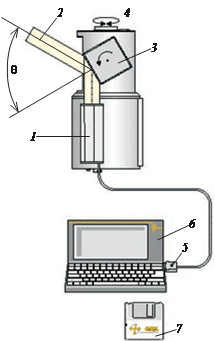 На рис. 8.21 показана прин- ципиальная схема трехмерного лазерного сканера, здесь 1 — ла- зерный дальномер; 2 — лазерный луч; 3 — вертикальная развертка (вращающаяся полигональная зеркальная призма); 4 — горизон- тальная развертка (вращающаяся оптическая головная часть скане- ра); 5 — кабель передачи данных; 6 — компьютер; 7 — программ- ное обеспечение.
На рис. 8.21 показана прин- ципиальная схема трехмерного лазерного сканера, здесь 1 — ла- зерный дальномер; 2 — лазерный луч; 3 — вертикальная развертка (вращающаяся полигональная зеркальная призма); 4 — горизон- тальная развертка (вращающаяся оптическая головная часть скане- ра); 5 — кабель передачи данных; 6 — компьютер; 7 — программ- ное обеспечение.
На рис. 8.22 показаны при- меры наиболее распространен- ных наземных лазерных скане- ров, а в табл. 8.1 приведены их характеристики.
рис. 8.21



 |  |  |
рис. 8.22
Т а б л и ц а 8.1
| Фирма изгото- витель | Марка | Изме- ряемые расстоя- ния, м | Поле зрения: горизон- тальное/ вертикальное, угл. градусы | Угловые интерва- лы, угл. градусы | Угловая точность, угл. градусы | линейная точность (для 50 м), мм | Скорость сканирова- ния, точек в секунду |
| Z+F | PROFILER 9012 | 0,3‒120 | 360/360 | 0,0007 | 0,02 | 2 | 1016 000 |
| Trimbl | TX8 | 0,6‒120 | 360/317 | 0,005 | 2 | 1016 000 | |
| Leica | HDS7000 | 0,3‒183 | 360/320 | 0,0004 | 0,007 | 0,8 | 1016 000 |
| Leica | ScanStation C10 | 1,5‒300 | 360/270 | 0,003 | 4 | 50 000 | |
| Faro | Focus 3D X330 | 0,6‒330 | 360/300 | 0,009 | 0,009 | 0,3 | 97 000 |
| Maptek | ISite 8200 | 1‒500 | 360/125 | 0,025 | 0,001 | 1 | 40 000 |
| Riegl | LMS-Z620 | 2‒2000 | 360/80 | 0,0025 | 5 | 11 000 | |
| Optech | ILRIS LR | 3‒3000 | 40/40 | 0,001 | 7 | 10 000 | |
| Riegl | VZ-6000 | 5‒6000 | 360/320 | 0,002 | 0,0005 | 15 | 222 000 |









