§8.1. Принцип формирования дискретной трехмерной модели объекта съемки лазерным сканером
Сканер предназначен для съемки различных объектов (зданий, со- оружений), местности и т.д. Результатом съемки является трехмерная модель объекта в виде совокупности точек, для каждой из которых определены пространственные координаты X, Y, Z и интенсивность отраженного сигнала d. все сканеры можно разделить по принципу действия на три группы: импульсные, фазовые и триангуляционные. Рассмотрим каждую из этих групп.
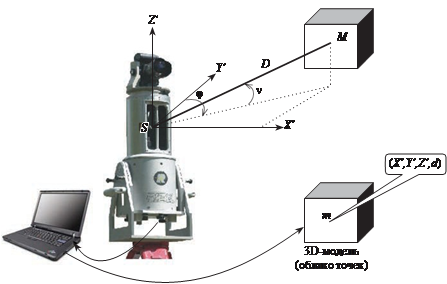
Импульсные и фазовые сканеры представляют собой устройство, объединяющее в себе теодолит, лазерный дальномер и сенсор. Таким образом, для любой точки объекта регистрируются горизонтальный j и вертикальный ν углы с помощью теодолита, расстояние D с помощью лазерного дальномера и интенсивность отраженного сигнала d дально- мера с помощью сенсора (рис. 8.1).
Задавая диапазон (jmin, νmin, jmax, νmax) и шаг (Dj, Dν) изменения го- ризонтальных и вертикальных углов, сканер автоматически с помощью моторов последовательно устанавливает луч лазера и регистрирует параметры j, ν, D и d для каждой точки объекта в заданных пределах. Точность установки Dj, Dν с помощью моторов ниже точности измерения углов j, ν, поэтому для каждой точки сканирования регистрируются значения j, ν.
Соответствующие координаты точек модели объекта вычисляются по известным формулам:
X ¢ = D cos nsin j;
Y ¢ = D cosn cos j;
Z ¢ = D sin n.
(8.1.1)
 Объект
Объект
рис. 8.1
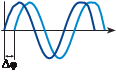
Координаты точек модели объекта X′, Y′, Z′ получаются в простран- ственной системе координат сканера (модели) SX′Y′Z′ (см. рис. 8.1). Эта система координат связана с системой отсчетов горизонтальных и верти- кальных углов в сканере и в общем случае произвольно ориентирована в пространстве. в зависимости от метода измерения расстояния D ска- неры можно разделить на две большие группы: импульсные и фазовые. И м п у л ь с н ы е с к а н е р ы основаны на измерении времени t (рис. 8.2, a) прохождения лазерного луча от сканера до объекта и об-
ратно. в этом случае расстояние вычисляется как:
D = vt , (8.1.2)
2
где v — скорость распространения электромагнитных волн.
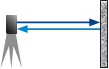
Ф а з о в ы е с к а н е р ы основаны на измерении разности фаз ∆φ (рис. 8.2, б) посылаемых и принимаемых модулированных сигналов и количества целых длин волн между сканером и объектом. Расстояние можно вычислить по формуле
 D = K l + Dj l, (8.1.3)
D = K l + Dj l, (8.1.3)
2p
где K — целое количество длин волн, укладывающихся на дан- ном расстоянии; λ — длина вол- ны; ∆φ — разность фаз между прямой и обратной волной.
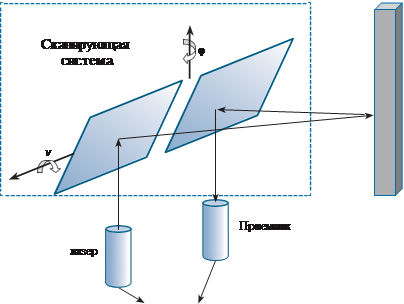
На рис. 8.3 показан принцип импульсного/фазового методов
 а б
а б
рис. 8.2
измерения расстояний наземным лазерным сканером. Сканирование осуществляется за счет вращения зеркал вокруг горизонтальной и вертикальной осей. лазерный луч проходит от излучателя до объекта и обратно до приемника. При этом измеряется время прохождения луча (для импульсного сканера) или фаза (для фазового сканера). Главное преимущество фазового метода измерения расстояний — более высокая точность и скорость съемки.
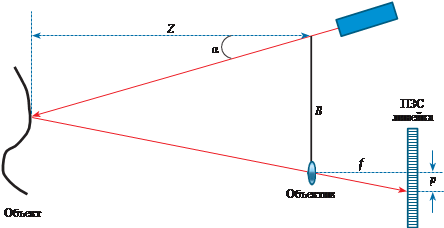
Т р и а н г у л я ц и о н н ы е с к а н е р ы. На рис. 8.4 показана прин- ципиальная схема лазерного сканера триангуляционного типа. Сканер
 Объект
Объект
 |
рис. 8.3
 лазер
лазер
рис. 8.4
состоит из лазера и камеры, фиксирующей положение отраженного от объекта лазерного пятна на линейке ПЗС. лазер и камера жестко за- фиксированы относительно друг друга на величину базиса В. Угловая ориентация сканера (луча сканера) относительно камеры (главной оп- тической оси камеры) также фиксирована, т.е. угол α = const.
Как следует из рис. 8.4 расстояние от сканера до объекта Z (отсто- яние) может быть вычислено по следующей формуле:
Z =B f ,
p + f tga
(8.1.4)
 Матрица ПЗС
Матрица ПЗС
лазер
Объектив
где f — фокусное расстояние ка- меры; р — координата изображе- ния пятна лазера на линейке ПЗС относительно главной точки.
На практике вместо лазера,
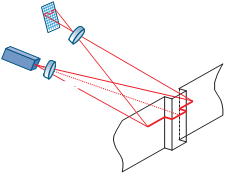
Проектирую- щая оптика
рис. 8.5
Объект
генерирующего луч, чаще ис- пользуют лазер, генерирующий плоскость и дающий на объекте след в виде линии, а вместо каме- ры, основанной на линейке ПЗС, используют камеру с матрицей ПЗС. Это дает возможность в

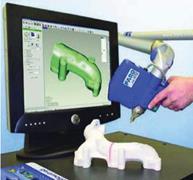
рис. 8.6
один момент времени измерять не одну точку объекта, а целый про- филь (рис. 8.5).
На рис. 8.6 показан пример триангуляционного сканера фирмы
«FARO», входящего в состав контрольно-измерительной машины (из- мерительной руки), которая позволяет задавать пространственное по- ложение и ориентацию сканера в любой момент времени.
Подобные системы позволяют строить трехмерные модели объек- тов в виде облака точек в режиме реального времени с высокой степенью точности (от микронов до десятых долей миллиметра в зависимости от отстояния). Максимальное отстояние для триангуляционных сканеров составляет примерно 5 м. Ожидаемую среднюю квадратическую ошибку определения координат точек модели m Z можно подсчитать по формуле
Z 2
 m Z »
m Z »
fB m p .
(8.1.5)
Здесь m p — средняя квадратическая ошибка измерения координат точек снимка, принадлежащих профилю (см. рис. 8.4). Эта величина в значительной степени зависит от разрешения камеры и от алгоритмов, применяемых для автоматического измерения координат точек снимков. Формула (8.1.5) получена на основе дифференцирования исходного урав- нения (8.1.4) по измеряемой величине р. Недостатком метода является высокая стоимость оборудования.
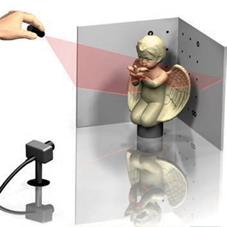
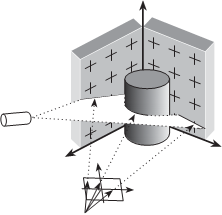
Рассмотрим другой подход к созданию трехмерных моделей объ- ектов, основанный на применении видеокамеры, лазера с плоской раз- верткой и тест-объекта с сетью опорных точек (рис. 8.7).
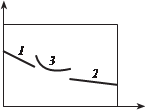
Суть метода заключается в следующем. Исследуемый объект (в данном случае это цилиндр) помещается на фоне тест-объекта (см. рис. 8.7). Тест-объект представляет собой две плоские пластины, жестко закрепленные между собой под прямым углом. На каждую из этих пластин нанесены маркированные точки (например, в виде крестов, окружностей и т.д.), координаты X,Y,Z которых определены заранее. Перед объектом устанавливается неподвижно цифровая видеокамера, которая постоянно его снимает. в это время оператор, держа в руке только лазер с плоской разверткой, сканирует весь объект. в результате на каждом снимке отображается след пересечения плоскости скани- рования с объектом 3 и тест-объектом 1 и 2 (рис. 8.8). Причем, если съемку выполнять в затемненном помещении, то на каждом снимке будет изображаться только этот след. Далее, применяя известные ал-
горитмы фильтрации изображе-
 Z
Z
P1
P3
|
X R1 R3
2
r3 x
|
r1
2
Sr
рис. 8.7
 y
y
ния, можно выделить пиксели, принадлежащие изображению следа пересечения объекта с плоскостью сканирования. За-
P2 тем для каждого пикселя вос- станавливают проектирующий луч r (см. рис. 8.7) и находят точку пересечения этого луча
с плоскостью сканирования P3.
Y в результате получается про-
филь объекта в виде набора то- чек с известными координатами X,Y,Z в системе координат тест- объекта. Затем плоскость скани- рования перемещают и получают следующий профиль и т.д. Кроме того можно поменять точку ска- нирования или повернуть объект и получить другую серию про- филей и т.д. в результате имеем 3D-модель исследуемого объекта в виде облака точек поверхности
o x
рис. 8.8
объекта с известными координа- тами X,Y,Z. При необходимости
можно присвоить каждой точке реальную яркость (цвет) изображения, взяв ее со снимков объекта, полученных при нормальном освещении.
Рассмотрим более подробно алгоритм получения координат X,Y,Z
точек объекта.
Этап 1. Определение элементов внешнего ориентирования снимков. Поскольку камера во время съемки стоит неподвижно, то все снимки будут иметь одинаковые элементы внешнего ориентирования, которые определяются путем решения обратной засечки по снимку тест-объекта. Для автоматизации процесса распознавания точек тест- объекта и измерения координат их изображений можно использовать
кодированные метки. Предварительно камера калибруется.
Этап 2. выделение пикселей на снимке (см. рис. 8.8), принад- лежащих изображению следа сечения плоскости сканирования P3 (см. рис. 8.7) с плоскостями тест-объекта P1, P2 и объекта исследова- ний не представляет никаких трудностей, т.к. яркости этих пикселей значительно отличаются от яркостей других пикселей. Теперь следует разделить все выделенные пиксели на три группы (см. рис. 8.8). Здесь 1, 2 — участки изображения следов сечения плоскости сканирования с плоскостями тест-объекта. Очевидно, что они на снимке изображают- ся в виде отдельных прямых. Это обстоятельство и используется для разделения пикселей на группы. Пиксели, которые не лежат на этих прямых, принадлежат изображению следа сечения плоскости скани- рования с объектом.
Этап 3. вычисление координат X,Y,Z точек, принадлежащих сле-
дам сечения плоскостей тест-объекта P1 и P2 с плоскостью сканирова-
ния P3. Другими словами вычисляются координаты векторов R1 и R2
(см. рис. 8.7) в системе координат объекта.
Координаты вектора R1 можно определить по известным формулам фотограмметрии:
æ X ö æ X S ö æ X ¢ ö
ç Y ÷ = ç Y S ÷ + N ç Y ¢ ÷, (8.1.6)
ç ÷ ç ÷ ç ÷
ç Z ÷ ç Z S ÷ ç Z ¢ ÷
è ø è ø è ø
æ X ¢ ö æ x - x0 ö
где
ç Y ¢ ÷ = A ç y - y0 ÷; x, y — координаты вектора (определены на
ç ÷ ç ÷
ç Z ¢ ÷ ç -f ÷
è ø è ø
предыдущем этапе); а — матрица поворота системы координат
снимка относительно системы координат объекта (определена в ре- зультате решения обратной засечки); X S, Y S, Z S — координаты цен- тра проекции (определены в результате решения обратной засечки);
x0, y0, f, d x, d y — координаты главной точки, фокусное расстояние и поправки за влияние дисторсии объектива (определяются в результате калибровки камеры); N — скаляр.
в уравнении (8.1.6) все величины известны, кроме скаляра N. Для его определения зададим плоскость P1 (см. рис. 8.7) следующим урав- нением:
AX + BY + CZ + D = 0. (8.1.7)
Коэффициенты A, B, C, D уравнения (8.1.7) находим по методу наи- меньших квадратов по точкам тест-объекта, у которых Y = const. Так как
координаты вектора R1 принадлежат этой плоскости, то можно записать
(подставляя (8.1.6) в (8.1.7)) следующее:
откуда
A( X S + NX ¢) + B(Y S + NY ¢) + C(Z S + NZ ¢) + D = 0,
(8.1.8)
 N = AX S + BY S + CZ S + D . (8.1.9)
N = AX S + BY S + CZ S + D . (8.1.9)
AX ¢ + BY ¢ + CZ ¢
Подставляя N, вычисленное по (8.1.9), в (8.1.6) получаем все три координаты точки, принадлежащей следу сечения плоскости P1 пло- скостью сканирования P3. аналогично получаем координаты всех точек, принадлежащих этому следу. Затем получаем координаты точек,
принадлежащих следу пересечения плоскости тест-объекта P2 с той
же плоскостью сканирования, т.е. координаты векторов R2 , исполь-
зуя при этом тот же алгоритм (8.1.6)–(8.1.9). Коэффициенты A, B, C, D уравнения (8.1.7) в этом случае определяются по точкам тест-объекта, у которых X = const.
Этап 4. Определение координат X,Y,Z точек, принадлежащих следу
сечения плоскости сканирования и объекта, т.е. определение координат векторов R3 .
Задача решается по тому же алгоритму (8.1.6)–(8.1.9), описанному выше. Коэффициенты A, B, C, D уравнения (8.1.7) плоскости сканиро-
вания P3 (см. рис. 8.7) определяются по методу наименьших квадратов,
используя точки, принадлежащие этой плоскости (вектора R1 и R2 ), которые определены на предыдущем этапе.
Этапы 2–4 повторяются для всех снимков, полученных видеокаме- рой. Оператор меняет положение и ориентацию лазера, облучая каждый раз различные участки поверхности исследуемого объекта. Если при этом объект оставался неподвижным, то все точки получаются в единой системе координат. в результате получается трехмерная модель объ- екта в виде плотного облака точек с координатами X,Y,Z. Если объект повернуть, так чтобы изучить поверхность объекта с другой стороны, то в результате получим модель объекта в другой системе координат. Для получения всего объекта в единой системе координат можно вос- пользоваться алгоритмами соединения трехмерных моделей, которые будут описанны в §8.3.
Этап 5. Получение яркости изображения (цвета) для каждой точки трехмерной модели объекта.
Соответствующие яркости (цвета) можно получить со снимка ис- следуемого объекта, используя известные уравнения коллинеарности:
x = x
- f a11( X - X S ) + a21(Y - Y S ) + a31(Z - Z S ) ;

0 a ( X - X ) + a
(Y - Y ) + a (Z - Z )
13 S 23
S 33 S
(8.1.10)
y = y
- f a12 ( X - X S ) + a22 (Y - Y S ) + a32 (Z - Z S ) ,

0 a ( X - X ) + a (Y - Y ) + a (Z - Z )
13 S 23 S 33 S
где X, Y, Z — координаты точки трехмерной модели объекта; x, y — ко- ординаты соответствующей точки на снимке.
|
По координатам x, y со снимка берется яркость (цвет) и присваивается соответствующей точке трехмерной модели. Для этих целей снимок может быть получен другой цифровой каме- рой с лучшим фотометрическим и геометрическим разрешением, чем у видеокамеры. Таким об- разом, получается 3D-модель объекта в реальном масштабе времени с реальными текстура- ми. На рис. 8.9 показан пример применения описанной выше
системы фирмы «DAVID».
рис. 8.9
Очевидно, что триангуляционные сканеры используются для по- лучения трехмерных моделей объектов в виде плотного облака точек для небольших по размерам объектов. Для изучения больших объектов применяют импульсные и фазовые сканеры.