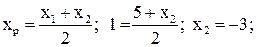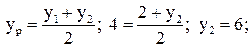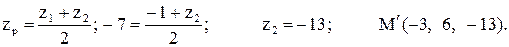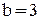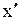2. Уравнение прямой ВС: ; ; .
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
«АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ»
Задача 1. Общее уравнение прямой на плоскости имеет вид
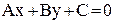 , (1)
, (1)
где А, В – координаты нормального (перпендикулярного) вектора прямой.
Уравнение прямой, проходящей через точку 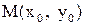 , перпендикулярно вектору
, перпендикулярно вектору 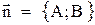 :
:
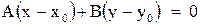 . (2)
. (2)
Уравнение прямой, проходящей через точку 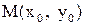 , параллельно вектору
, параллельно вектору 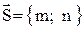 , имеет вид
, имеет вид
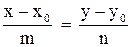 . (3)
. (3)
Уравнение прямой, проходящей через две заданные точки 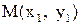 и
и 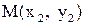 :
:
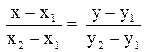 (4)
(4)
Уравнение прямой, проходящей через данную точку 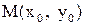 в данной направлении, имеет вид
в данной направлении, имеет вид
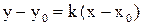 (5)
(5)
где 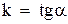 - угловой коэффициент прямой,
- угловой коэффициент прямой, 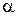 - угол, образованный прямой с положительным направлением на оси ОХ.
- угол, образованный прямой с положительным направлением на оси ОХ.
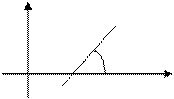 у
у
|
х
Если прямая проходит через начало координат, то ее уравнение имеет вид
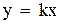 . (6)
. (6)
Уравнение 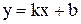 (7)
(7)
называется уравнением прямой с угловым коэффициентом, где b – величина отрезка, отсекаемого прямой от оси ОУ.
у
b 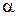
х
Пусть две прямые заданы общими уравнениями
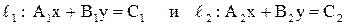 .
.
Если 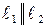 , то
, то 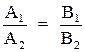 .
.
Если 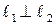 , то
, то 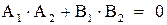 .
.
Если 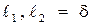 , то
, то 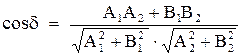 .
.
Пусть две прямые заданы уравнениями с угловым коэффициентом
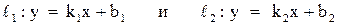 .
.
Если 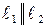 , то
, то 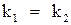 .
.
Если 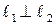 , то
, то 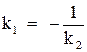 .
.
Если 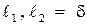 , то
, то 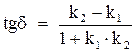 .
.
Расстояние 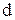 от точки
от точки 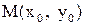 до прямой
до прямой 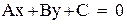 вычисляется по формуле
вычисляется по формуле
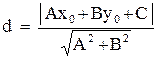 (8)
(8)
Пример 1
Даны координаты вершин треугольника 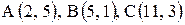 .
.
1) Вычислить длину стороны 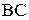 .
.
2) Составить уравнение линии 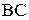 .
.
3) Составить уравнение высоты, проведенной из вершины А, и найти ее длину.
4) Найти точку пересечения медиан.
5) Найти косинус внутреннего угла при вершине В.
6) Найти координаты точки М, расположенной симметрично точке А, относительно прямой ВС.
 А
А
О
В С
М
Решение
1. Длина стороны ВС равна модулю вектора 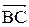 .
.
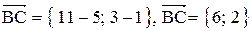 ;
; 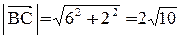 .
.
2. Уравнение прямой ВС: 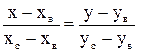 ;
; 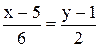 ;
; 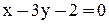 .
.
3. Уравнение высоты АК запишем как уравнение прямой, проходящей через точку 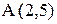 перпендикулярно вектору
перпендикулярно вектору 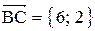 :
: 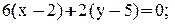
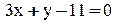 . Длину высоты АК можно найти как расстояние от точки А до прямой ВС:
. Длину высоты АК можно найти как расстояние от точки А до прямой ВС: 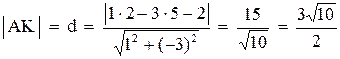 .
.
4. Найдем координаты точки N – середины стороны ВС:
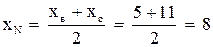 ;
; 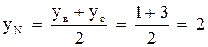 ;
; 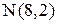 .
.
Точка пересечения медиан О делит каждую медиану на отрезки в отношении 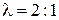 .
.
Используем формулы деления отрезка в данном отношении 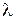 :
:
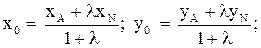
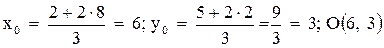 .
.
5. Косинус угла при вершине В найдем как косинус угла между векторами 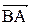 и
и 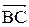
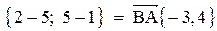 ;
; 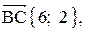
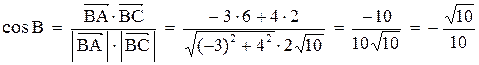 .
.
6. Точка М, симметричная точке А относительно прямой ВС, расположена на прямой АК, перпендикулярной к прямой ВС, на таком же расстоянии от прямой, как и точка А. Координаты точки К найдем как решения системы 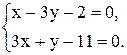 Систему решим по формулам Крамера:
Систему решим по формулам Крамера: 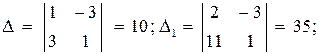
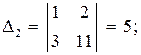
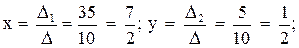
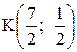 .
.
Точка К является серединой отрезка АМ.
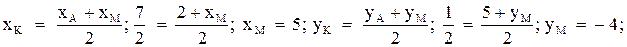
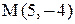 .
.
Пример 2
Через точку М(3, 5) провести прямую так, чтобы она отсекала от координатного угла равнобедренный треугольник.
«Провести прямую» - это значит записать уравнение прямой, при этом делать чертеж и проводить прямую не обязательно.
Будем искать уравнение прямой в отрезках, т. е. в форме 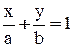 , где a и b – величины отрезков, отсекаемых прямой на осях координат. По условию задачи
, где a и b – величины отрезков, отсекаемых прямой на осях координат. По условию задачи 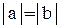 и прямая проходит через точку М(3, 5). Следовательно,
и прямая проходит через точку М(3, 5). Следовательно, 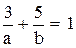 . Для определения а и b имеем две системы:
. Для определения а и b имеем две системы: 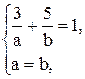 и
и 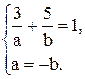
Решение первой системы: 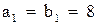 , решение второй системы:
, решение второй системы: 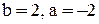 . Получаем две прямые:
. Получаем две прямые: 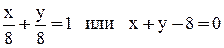 и
и 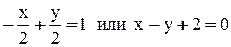
З а д а ч а 3
Канонические уравнения кривых второго порядка имеют вид
1) 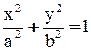 - эллипс с фокусами
- эллипс с фокусами 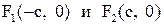 , где
, где 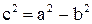 , и эксцентриситетом
, и эксцентриситетом 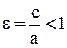 . Если
. Если 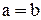 , то уравнение
, то уравнение 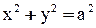 описывает окружность, в этом случае
описывает окружность, в этом случае 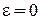 ;
;
2) 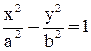 - гипербола с фокусами
- гипербола с фокусами 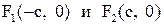 , где
, где 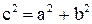 , и эксцентриситетом
, и эксцентриситетом 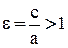 . Прямые
. Прямые 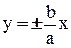 являются асимптотами гиперболы;
являются асимптотами гиперболы;
3) 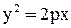 - парабола, симметричная оси Ох, с фокусом
- парабола, симметричная оси Ох, с фокусом 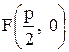 и директрисой
и директрисой 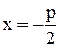 ,
, 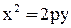 - парабола, симметричная относительно Оу, с фокусом
- парабола, симметричная относительно Оу, с фокусом 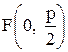 и директрисой
и директрисой 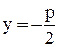 .
.
Пример 3
Составить уравнение параболы с вершиной в начале координат, если ее директриса параллельна оси Оу и проходит через левый фокус гиперболы:
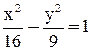 .
.
Определим координаты левого фокуса гиперболы: 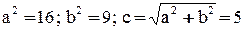 ,
, 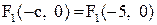 . Так как директриса параболы параллельна оси Оу и проходит через точку
. Так как директриса параболы параллельна оси Оу и проходит через точку 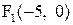 , то она имеет уравнение
, то она имеет уравнение 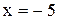 . Определим значение параметра р параболы:
. Определим значение параметра р параболы: 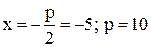 . Каноническое уравнение параболы имеет вид
. Каноническое уравнение параболы имеет вид 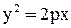 , т. е.
, т. е. 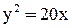 .
.
З а д а ч а 4
Нормальные уравнения кривых второго порядка с центром в точке 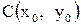 имеют вид
имеют вид
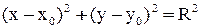 - окружность радиусом R;
- окружность радиусом R;
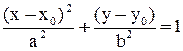 - эллипс с полуосями а и b;
- эллипс с полуосями а и b;
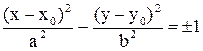 - гипербола;
- гипербола;
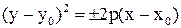 или
или 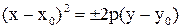 - парабола.
- парабола.
Пример 4
Дано уравнение линии 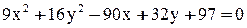 . Записать уравнение линии в нормальной форме и построить эту кривую.
. Записать уравнение линии в нормальной форме и построить эту кривую.
Чтобы привести уравнение к нормальной форме, сгруппируем слагаемые, содержащие только х и у, вынося коэффициенты при 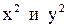 за скобки:
за скобки:
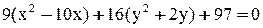 .
.
Дополняем выражения в скобках до полных квадратов:
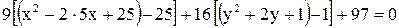 ;
;
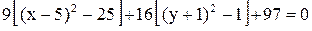 ;
;
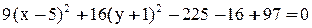 ;
;
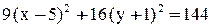 .
.
Разделив обе части на 144, получим нормальное уравнение эллипса:
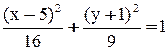 с полуосями
с полуосями 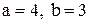 с центром в точке
с центром в точке 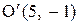 . Через точку
. Через точку 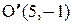 проведем новые оси координат (
проведем новые оси координат ( 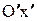 и
и 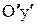 ) параллельные соответственно осям Ох и Оу. По обе стороны от точки
) параллельные соответственно осям Ох и Оу. По обе стороны от точки 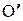 отложим по оси
отложим по оси 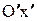 отрезки длиной
отрезки длиной 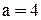 , а по оси
, а по оси 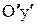 -
- 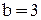 , получив таким образом вершины эллипса. Проведя через вершины вспомогательные отрезки, параллельные осям, получим прямоугольник, в который нужно вписать эллипс. Чертим эллипс.
, получив таким образом вершины эллипса. Проведя через вершины вспомогательные отрезки, параллельные осям, получим прямоугольник, в который нужно вписать эллипс. Чертим эллипс.
 у
у 

 х
х
|

|
|
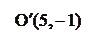
|
Координаты фокусов эллипса в новых осях: 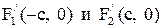 . Здесь
. Здесь 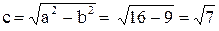 . Старыми координатами фокусов будут
. Старыми координатами фокусов будут 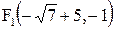
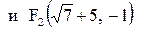 , т. к.
, т. к. 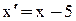 и
и 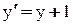
З а д а ч а 5
Общее уравнение плоскости имеет вид: 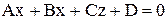 , где
, где 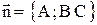 - ненулевой вектор, перпендикулярный плоскости (нормальный вектор плоскости).
- ненулевой вектор, перпендикулярный плоскости (нормальный вектор плоскости).
Уравнение плоскости, проходящей через три данные точки 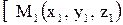 ,
, 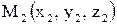 и
и 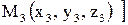 определяется равенством
определяется равенством
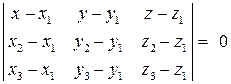 .
.
Расстояние от точки 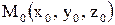 до плоскости
до плоскости 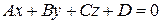 находится по формуле
находится по формуле 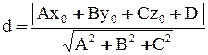 .
.
Пример 5
Найти расстояние от точки 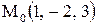 до плоскости, проходящей через точки
до плоскости, проходящей через точки 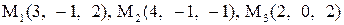 .
.
Найдем уравнение плоскости, проходящей через точки 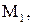
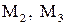 :
:
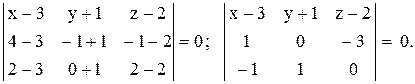
Вычислим определитель, разложив его по первой строке:
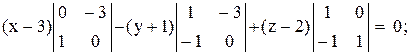
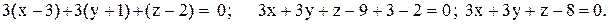
Найдем расстояние от точки  до плоскости
до плоскости 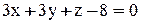 .
.
З а д а ч а 6
Косинус угла 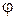 между плоскостями
между плоскостями 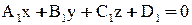 и
и 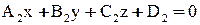 вычисляется по формуле
вычисляется по формуле
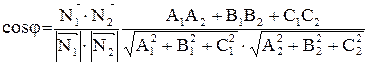 .
.
Пример 6
Найти угол между плоскостями 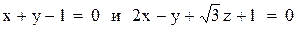 .
.
Найдем косинус искомого угла:
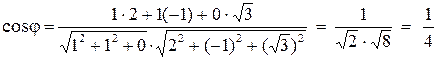 ,
, 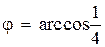 .
.
З а д а ч а 7
Канонические уравнения прямой в пространстве имеют вид
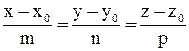 , (9)
, (9)
где 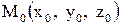 - точка, лежащая на прямой, а
- точка, лежащая на прямой, а 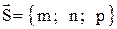 - направляющий вектор прямой (ненулевой вектор, параллельный прямой).
- направляющий вектор прямой (ненулевой вектор, параллельный прямой).
Чтобы перейти от общих уравнений прямой
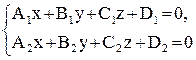 (10)
(10)
к ее каноническим уравнениям, нужно на прямой найти какую-нибудь точку 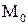 и определить направляющий вектор прямой
и определить направляющий вектор прямой 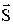 . Точку
. Точку 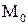 можно найти так: задаем произвольно значение одной переменной, например,
можно найти так: задаем произвольно значение одной переменной, например, 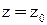 , и из общих уравнений прямой (10) найдем значения
, и из общих уравнений прямой (10) найдем значения 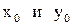 . Направляющий вектор
. Направляющий вектор 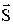 параллелен
параллелен
линии пересечения плоскостей (10) и, следовательно, перпендикулярен векторам 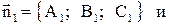
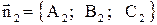 . Поэтому в качестве
. Поэтому в качестве 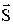 можно взять вектор
можно взять вектор
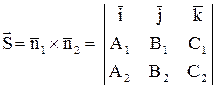 .
.
Пример 7
Написать канонические уравнения прямой 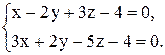
Найдем точку 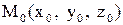 , лежащую на прямой. Пусть
, лежащую на прямой. Пусть 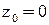 .
.
Тогда 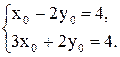
Решив систему, найдем 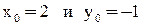 . Таким образом,
. Таким образом, 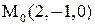 . Найдем направляющий вектор прямой
. Найдем направляющий вектор прямой
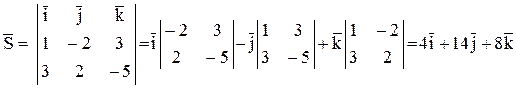 .
.
Запишем канонические уравнения: 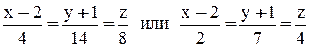 .
.
З а д а ч а 8
Точка пересечения Р прямой и плоскости находится следующим образом: уравнения прямой приводят к параметрическому виду 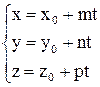 , затем подставляют в уравнение плоскости
, затем подставляют в уравнение плоскости 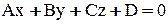 и определяют значение параметра t , соответствующее точке пересечения. Если при такой подстановке уравнение плоскости выполняется при любом t, то прямая лежит в плоскости, а если не выполняется ни при каком t, то прямая параллельна плоскости. Найденное значение t подставляют в параметрические уравнения прямой.
и определяют значение параметра t , соответствующее точке пересечения. Если при такой подстановке уравнение плоскости выполняется при любом t, то прямая лежит в плоскости, а если не выполняется ни при каком t, то прямая параллельна плоскости. Найденное значение t подставляют в параметрические уравнения прямой.
Пример 8
Найти точку пересечения прямой 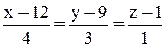 и плоскости
и плоскости 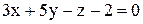 .
.
Приведем уравнения прямой к параметрическому виду:
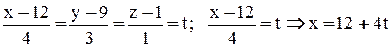 ;
; 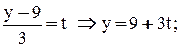
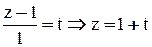 , т. е. параметрические уравнения прямой имеют вид
, т. е. параметрические уравнения прямой имеют вид
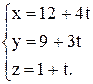
Подставив х, у, z в уравнение плоскости, найдем t:
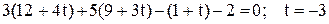 .
.
Искомая точка пересечения прямой и плоскости имеет координаты
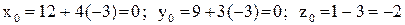 , т. е.
, т. е. 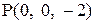 .
.
З а д а ч а 9
Чтобы найти точку 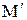 , симметричную точке
, симметричную точке 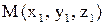 относительно прямой, нужно найти проекцию точки М на прямую
относительно прямой, нужно найти проекцию точки М на прямую 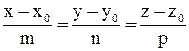 . Проекция будет серединой отрезка
. Проекция будет серединой отрезка  . Проекция есть точка пересечения прямой с перпендикулярной к ней плоскостью, проходящей через точку М. Так как вектор
. Проекция есть точка пересечения прямой с перпендикулярной к ней плоскостью, проходящей через точку М. Так как вектор 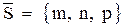 перпендикулярен этой плоскости, ее уравнение запишем в виде
перпендикулярен этой плоскости, ее уравнение запишем в виде
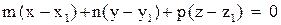 .
.
Далее, как и в предыдущей задаче, находим точку Р (точку пересечения данной прямой с найденной плоскостью). Зная середину отрезка 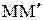 , найдем координаты точки
, найдем координаты точки 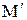 . Чтобы найти точку
. Чтобы найти точку 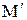 , симметричную точке
, симметричную точке 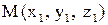 относительно плоскости
относительно плоскости 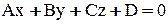 , нужно найти проекцию точки М на плоскость. Проекция будет серединой отрезка
, нужно найти проекцию точки М на плоскость. Проекция будет серединой отрезка 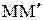 .
.
Проекция точки 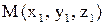 на плоскость будет точкой пересечения перпендикуляра к плоскости, проходящего через точку М, с самой плоскостью. Вектор
на плоскость будет точкой пересечения перпендикуляра к плоскости, проходящего через точку М, с самой плоскостью. Вектор 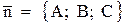 будет направляющим вектором перпендикулярной прямой.
будет направляющим вектором перпендикулярной прямой.
Далее, как и в задаче 9, находим точку пересечения перпендикуляра с данной плоскостью.
Зная середину отрезка 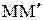 , найдем координаты точки
, найдем координаты точки 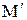 .
.
Пример 9
Найти точку 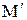 , симметричную точке
, симметричную точке 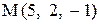 относительно плоскости
относительно плоскости 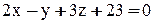 .
.
Запишем канонические уравнения перпендикуляра  к плоскости. Вектор
к плоскости. Вектор 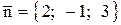 будет направляющим вектором перпендикуляра
будет направляющим вектором перпендикуляра
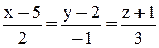 .
.
Параметрические уравнения прямой 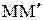 :
: 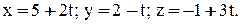 Подставляя х, у, z из этих уравнений в данное уравнение плоскости, найдем значение t:
Подставляя х, у, z из этих уравнений в данное уравнение плоскости, найдем значение t:
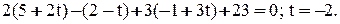
Точка Р пересечения прямой с плоскостью будет иметь координаты
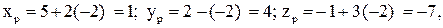 т. е.
т. е. 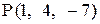 .
.
Так как Р – середина отрезка 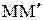 и
и 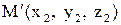 - координаты, так как если то
- координаты, так как если то