§7.7. определение приближенных значений элементов внешнего ориентирования снимков

Дата: 2025-06-02; Просмотры: 20

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

(7.6.10)

Как было показано выше, в общем случае элементы внешнего ориентирования снимков во время съемки могут принимать произволь- ные значения. Например, угловые элементы внешнего ориентирования снимков могут варьироваться от 0 до 360°. Решение фотограмметри- ческих задач (прямая и обратная засечки, взаимное ориентирование пары снимков, внешнее ориентирование модели и фототриангуляция) выполняются методом последовательных приближений, который тре- бует знания приближенных значений неизвестных элементов внешнего ориентирования снимков.

Существует достаточно много различных способов решения этой задачи. Самый простой из них это получение приближенных значений элементов внешнего ориентирования со схемы съемки, которая рисуется на бумаге или в специальном программном обеспечении, где оператор расставляет на экране компьютера точки съемки вокруг объекта. Коор- динаты центров проекции снимаются с этой схемы в заданной системе координат, а углы наклона камеры вычисляются в этой системе коорди- нат после того как оператор задаст направление съемки с данной точки. Если известны координаты опорных точек, то приближенные зна- чения элементов внешнего ориентирования снимка можно вычислить

на основе известных уравнений проективных преобразований:

x = L1 X + L2Y + L3Z + L4 ; y = L5 X + L6Y + L7Z + L8 , (7.7.1)

L9 X + L10Y + L11Z + 1 L9 X + L10Y + L111Z + 1

где x, y — координаты точки на снимке; X,Y,Z — координаты соответ- ствующей точки на объекте; L1, …, L11 — коэффициенты проективных преобразований.

Уравнения (7.7.1) можно переписать следующим образом:

L1 X + L2Y + L3Z + L4 - xXL9 - xYL10 - xZL11 - x = v x ;

L X + LY + L Z + L

- y XL

- y YL

- y ZL

- y = v . (7.7.2)

5 6 7 8 9 10 11 y

Уравнения (7.7.2) линейны относительно неизвестных коэффици- ентов проективных преобразований. Эти уравнения составляют для всех опорных точек и решают по методу наименьших квадратов. в результате находят значения всех одиннадцати коэффициентов, при- чем минимальное количество опорных точек в этом случае равно пяти.

Если известны коэффициенты проективных преобразований, то по ним можно вычислить элементы внутреннего и внешнего ориенти- рования снимка по следующим формулам:

x = (L L + L L + L L )L2; y = (L L + L L + L L )L2;

0 1 9 2 10 3 11 0 5 9 6 10 7 11

f = (L2 + L2 + L2 )L2 - X 2 ; f = (L2 + L2 + L2 )L2 - Y 2 ;

x 1 2 3 S y 5 6 7 S

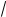
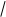a= sin-1(L L); w= (1-gt -L L ); a = L(x L - L ) f ;

9 10 11 11 0 9 1 x

(7.7.3)

é X ù é L L L ù-1 éL ù

ê ú ê

1 2 3 -1

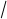
k= cos-1(a ) cos a; êY ú = êL L L ú êL ú , ãäå L =.

11 S

5 6 7 8

L2 + L2

+ L2

êëZ S úû

êëL9

L10

L11 úû

êë 1 úû

9 10 11

Формулы (7.7.3) получены путем преобразований уравнений (7.7.1) и известных уравнений коллинеарности. Таким образом, вычисляют элементы внешнего и внутреннего ориентирования снимка, используя прямые формулы. Здесь надо иметь в виду то обстоятельство, что опор- ные точки не должны располагаться в одной плоскости. Ограничение связано с тем, что в этом случае при решении системы уравнений (7.7.2) возникает неопределенность, так как коэффициенты проективных преобразований сильно коррелируют между собой из-за того, что они зависят от элементов внутреннего и внешнего ориентирования снимка. Одновременное нахождение этих двух групп неизвестных по опорным точкам, расположенным в одной плоскости, приводит к многозначно- сти решения. Эта проблема была освещена при рассмотрении вопроса калибровки камеры по тест-объекту (см. §7.3).

Рассмотрим другой вариант получения приближенных значений неизвестных. Предположим, что съемка объекта ведется таким образом, что всю совокупность снимков можно разделить на отдельные стере- опары. взаимные углы наклона снимков, составляющих стереопару, желательно выбирать небольшими, с тем чтобы можно было организо- вать стереоизмерения координат точек снимков. Однако это требование необязательно, т.к. взаимное ориентирование пары снимков можно вы- полнить при больших углах наклона.

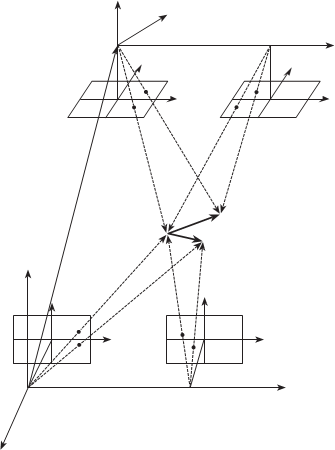
На рис. 7.35 показаны две стереопары, произвольно ориентирован- ные относительно друг друга, но имеющие перекрытие. Наша задача получить приближенные значения элементов внешнего ориентирования всех снимков на основе прямых формул. Данная задача решается в три этапа: 1) сначала выполняют взаимное ориентирование пар снимков и построение независимых моделей; 2) затем эти модели объединяют в общую модель объекта; 3) общая модель объекта ориентируется внешне и вычисляются элементы внешнего ориентирования всех снимков. Рас- смотрим каждый из этих этапов более подробно.

в з а и м н о е ор и е н т и р о в а н и е с т е р е о па р выполняется известным способом независимо друг от друга и получают модели в своих системах координат S1XYZ и S3XYZ. На рис. 7.35 точки первой модели обозначены M1 и M2, а второй — M1 и М′2. Этот этап не вызывает никаких затруднений. в качестве начальных приближений элементов взаимного ориентирования можно взять нули.

Z

Y

S4

3

y y

x x

Z R3

R S3

O X

Y

y

R3M

M1 R1M

M2

R1

y

M'2

x x

X

S1 S2

Z

рис. 7.35

О б ъ е д ин е ни е о т д е ль ны х м о д е л е й в общую модель объекта выполняется на основе известных уравнений перехода из одной системы координат в другую. Предположим, что общая модель объекта будет строиться в системе координат первой модели S1XYZ. Тогда пере- ход из системы координат второй модели в систему координат первой можно записать следующим образом (см. рис. 7.35):

  

R1 = R S + A3R3t, (7.7.4)

где



R1 и



R3 — векторы, определяющие положение точки М1 модели в

системе координат S1XYZ и S3XYZ соответственно; R S — вектор, зада-

ющий положение начала системы координат S3XYZ относительно S1XYZ;

а3 — матрица поворота одной системы координат относительно другой;

t — масштабный коэффициент второй модели относительно первой.

в уравнении (7.7.4) неизвестными являются R S , а3, t. Для их на-

хождения сначала перенесем начала систем координат первой и второй моделей S1XYZ и S3XYZ в любую из общих точек, например, в точку М1. Тогда (7.7.4) преобразуется к виду:

 

R1M = A3R3M t,

 

(7.7.5)

где R1M и R3M — векторы, определяющие положение соответствующих

точек моделей М2 и М′2 в системах координат параллельных системам координат S1XYZ и S3XYZ с началом в точке М1.

введем обозначения:

тогда 

C = At, (7.7.6)



R1M = С R3M . (7.7.7)

в координатной форме (7.7.7) запишется:

æ X ö

ç Y ÷

æ c11

= ç c21

c12 c22

c13 öæ X ö

c23 ÷ç Y ÷

. (7.7.8)

ç ÷ ç ÷ç ÷

ç Z ÷

ç c31

c32

c33 ÷ç Z ÷

è ø1M è øè ø3M

Уравнения (7.7.8) являются линейными, они позволяют найти сразу элементы матрицы С , т.е. найти направляющие косинусы, умноженные на масштабный коэффициент (7.7.6). Для нахождения этих элементов, как видно из (7.7.8), достаточно три общие точки. Уравнения составляются отдельно по каждой оси координат для n общих точек двух моделей:

æ X1 ö

æ X1 .

X n ö

ç ÷ = (c11

c12

c13 )ç Y1

. Y n ÷

. (7.7.9)

ç X n ÷

ç Z1 .

Z n ÷

è ø1M è ø3M

Решая (7.7.9), найдем первую строку матрицы С, т.е. элементы c11, c12, c13. аналогично найдем вторую и третью строчки матрицы С, составляя и решая систему уравнений по осям Y1M и Z1M:

æ Y1 ö

ç : ÷

= (c21

c22

æ X1 .

c23 )ç Y1 .

X n ö

Y n ÷

; (7.7.10)

ç ÷ ç ÷

çY n ÷

ç Z1 .

Z n ÷

è ø1M è ø3M

æ Z1 ö

æ X1 .

X n ö

ç ÷ = (c31

c32

c33 )ç Y1

. Y n ÷

. (7.7.11)

ç Z n ÷

ç Z1 .

Z n ÷

è ø1M è ø3M

вследствие естественных ошибок, которые присущи координатам X,Y,Z точек моделей, у найденной таким образом матрицы С векторы- строки могут не образовывать ортогональной системы (скалярные произведения векторов-строк должны быть равны нулю). Поэтому при нахождении второй строки матрицы С к системе уравнений (7.7.10) следует добавить следующее уравнение:

0 = c21c11 + c22c12 + c23c13

(7.7.12)

с известными c11, c12, c13 и решить совместно. К системе уравнений (7.7.11) добавляют уравнения

0 = c31c11 + c32c12 + c33c13;

0 = c31c21 + c32c22 + c33c23

(7.7.13)

с известными уже элементами c11, c12, c13 и c21, c22, c23, которые также решают совместно.

Теперь надо выделить из матрицы С масштабный коэффициент и получить ортогональную матрицу а. Для этого воспользуемся одним из условий ортогональности матрицы а, например, следующим:

a2 + a2 + a2 = 1

(7.7.14)

11 12 13

æ c ö2

æ c ö2

æ c ö2

или, согласно (7.7.6), ç

11 ÷ + ç

12 ÷ + ç

13 ÷ = 1. Отсюда

è t ø è t ø

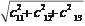t =

è t ø

; (7.7.15)

A = 1C. (7.7.16)

t

Зная значение ортогональной матрицы поворота а, всегда можно получить углы наклона и поворота одной модели относительно другой по элементам этой матрицы (см. главу 1).

Теперь, используя (7.7.5) или (7.7.7), осуществим переход из системы координат второй модели в систему координат первой и выполним обрат- ный перенос начала системы координат из точки М1 в точку S1. аналогич- но можно ориентировать остальные модели и получить общую модель объекта в единой системе координат S1XYZ. Далее по аналогичной схеме можно перейти к системе координат объекта OXYZ (см. рис. 7.35), т.е. выполнить внешнее ориентирование общей модели по опорным точкам. Если необходимо узнать ориентацию каждого снимка в системе координат объекта, то достаточно перемножить соответствующие ма-

трицы поворота. Так, например, для снимка S3 имеем

A3 = A0AA¢3 , (7.7.17)

где а3 — искомая матрица поворота системы координат снимка S3x yz относительно системы координат объекта; а0 — матрица поворота си- стемы координат общей модели S1XYZ относительно системы координат объекта OXYZ (получается в результате внешнего ориентирования об- щей модели); а — матрица поворота системы координат второй модели S3XYZ относительно системы координат исходной модели S1XYZ (полу- чается по формуле (7.7.16)); а′3 — матрица поворота системы координат снимка S3x yz относительно S3XYZ (получается в результате взаимного ориентирования стереопары).

л и не й н ые э л е ме н т ы в не ш не г о о р ие н т и р о в а н и я снимков X S,Y S,Z S в системе координат объекта OXYZ можно вычислить по следующей формуле:

æ X S ö æ X S1 ö æ X S ö

ç Y S ÷ = ç Y S1 ÷ + A0 ç Y S ÷

t, (7.7.18)

ç ÷ ç ÷ ç ÷

ç Z S ÷

ç Z S1 ÷

ç Z S ÷

è ø è ø è øM

где X S1,Y S1,Z S1 — координаты начала системы координат общей модели относительно системы координат объекта; (X SY SZ S)М — координаты центра проекции любого снимка в системе координат общей модели (получаются в результате объединения отдельных моделей); t — мас- штабный коэффициент общей модели (получается в результате внешнего ориентирования общей модели).

Таким образом, изложенный метод последовательного построения общей модели объекта в единой системе координат позволяет получить элементы внешнего ориентирования всех снимков, произвольно ори-

ентированных в этой системе координат, которые можно использовать в качестве начальных приближений для дальнейшего их совместного уравнивания.