§7.6. особенности фотограмметрической обработки наземных снимков
Фотограмметрическая обработка одиночных и стереопар назем- ных снимков производится таким же образом, что и обработка аэро- и космических кадровых снимков, то есть методами прямой, обратной
рис. 7. 33
и двойной обратной фотограмметрической засечки, методом связок, а также построением маршрутной и блочной фототриангуляции. в качестве опорной информации при фотограмметрической обработке
наземных снимков, так же как и при обработке аэрокосмических сним- ков используют координаты опорных точек и центров проекции снимков и значения угловых элементов внешнего ориентирования снимков.
При наземной фотограмметрической съемке зданий, инженерных сооружений и других объектов в качестве опорной информации мож- но использовать измеренные длины отрезков между точками объекта, точками фотографирования, точками фотографирования и точками объекта. Так же в качестве опорной информации можно использовать принадлежность точек объекта, изобразившихся на стереопаре снимков, вертикальному или горизонтальному объектам, горизонтальной пло- скости. Опорной информацией могут служить и опорные направления
— значения дирекционного и вертикального углов, определенных из точки фотографирования на точку объекта, изобразившейся на снимке.
При построении сети фототриангуляции по наземным снимкам или фотограмметрической обработке стереопары таких снимков, в случае, если была измерена длина отрезка D i между точками объекта, координаты изображений которых измерены на стереопарах снимков, для каждого такого отрезка составляется условное уравнение
- 
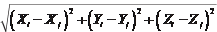D ij
= 0, (7.6.1)
в котором X i, Y i, Z i — координаты точки i объекта; X j, Y j, Z j — координаты точки j объекта.
в случае, если была измерена длина базиса фотографирования В
составляется условное уравнение
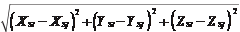- B = 0, (7.6.2)
в котором X Si, Y Si, Z Si и X Sj, Y Sj, Z Sj — координаты центров проекции i и j
снимков стереопары.
Если были измерены отрезки D i от центра проекции S i до точки объекта i составляется условное уравнение
- 
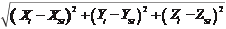D i
= 0, (7.6.3)
где X i, Y i, Z i — координаты точки i объекта; X Si, Y Si, Z Si — координаты
i-го центра проекции.
Если на стереопаре наземных снимков были измерены координа- ты изображений двух точек объекта, расположенных на вертикальной
прямой, то составляют условные уравнения
X i - X j = 0; Y i - Y j = 0, (7.6.4)
в которых X i, Y i — координаты точки i объекта; X j, Y j — координаты точки j объекта.
в случае, если на стереопаре наземных снимков измерены коорди- наты изображений точек объекта, расположенных на горизонтальной плоскости, то для любой пары точек составляют условное уравнение
Z i ‒ Z j = 0, (7.6.5)
в котором Z i и Z j — значения высот i и j точек объекта.
Принадлежность точек объекта i, j, k плоскости, произвольно ори- ентированной в пространстве (например, точки, принадлежащие стене здания), можно записать следующим образом:
X i - X j X i - X k X j - X k
Y i - Y j Y i - Y k Y j - Y k
Z i - Z j Z i - Z k Z j - Z k
= 0. (7.6.6 )
Уравнение поправок, соответствующее условному уравнению (7.6.1), имеет вид
в котором l D
dD + l D = v D , (7.6.7)
= D0 ‒ D; D0 — приближенное значение длины отрезка;
D — измеренное значение длины отрезка.
Уравнения поправок, соответствующие условным уравнениям (7.6.2) – (7.6.6), получают аналогично.
Если при выполнении назем-
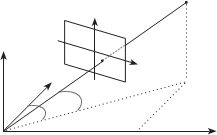ной фотограмметрической съемки M
в качестве опорной информации y D
с точек фотографирования были P
измерены дирекционные j и вер-
Z Z–Z S
тикальные ν углы на точки сни- маемого объекта, изобразившиеся на снимке (рис. 7.34), для точки объекта на которую измерены эти
углы можно составить известные S
уравнения коллинеарности:
m
Y
ν
φ
X–X S
x
M0
Y–Y S
X
рис. 7. 34
x = x
- f a11( X - X S ) + a21(Y - Y S ) + a31(Z - Z S ) ;
0 a ( X - X ) + a
(Y - Y ) + a (Z - Z )
13 S 23
S 33 S
(7.6.8)
y = y
- f a12 ( X - X S ) + a22 (Y - Y S ) + a32 (Z - Z S ) .
0 a ( X - X ) + a
(Y - Y ) + a (Z - Z )
13 S 23
Из рис. 7.34 следует, что
S 33 S
X - X S = D cos nsin j;
Y - Y S = D cosn cos j;
Z - Z S = D sin n.
Подставив значения X ‒ X S, Y ‒ Y S, Z ‒ Z S в уравнения коллинеарности (7.6.8), после преобразований получим уравнения
x = x
- f a11 cos nsin j + a21 cos ncosj + a31 sin n ;
0 a cos nsin j + a
cos ncosj + a sin n
13 23
33 (7.6.9)
y = y
- f a12 cos nsin j + a22 cos ncosj + a32 sin n .
0 a cos nsin j + a cosn cos j + a
sin n
13 23 33
Уравнения (7.6.9) называют уравнениями к о л л и н е а р н о с т и в п о л я р н ы х к о ор д и на т а х. в этих уравнениях неизвестными являются угловые элементы внешнего ориентирования снимка w, a, κ. Очевидно, что для их определения необходимо измерить на снимке ко- ординаты изображений не менее двух точек объекта, на которые были измерены дирекционный и вертикальный углы.
Уравнения поправок, соответствующие условным уравнениям (7.6.9), имеют вид:
a1dw + a2da + a3dk + l x = v x ;
b1dw + b2da + b3dk + l y = v y .