Калибровка цифровых фотокамер по снимкам пространственного тест-объекта
в этом методе фотограмметрическая калибровка цифровых фото- камер производится по снимкам пространственного тест-объекта. Тест-объект представляет собой пространственное поле маркированных точек. Наиболее оптимальным вариантом конструкции пространствен- ного тест-объекта служит тест-объект, представленный на рис. 7.13. Этот тест-объект может быть смонтирован в прямоугольном помещении с размерами по осям X и Y от 2,5 до 5 м, а по оси Z от 6 до 10 м.
На дальней от съемочной камеры стене помещения жестко укре- пляют маркированные точки, равномерно расположенные по площади. Кроме того, на верхней, нижней и боковых стенах помещения укрепля-
ют ряды маркированных точек в сечениях стен плоскостями параллельными плоскости даль- ней стены. Максимальное рас- стояние между маркированными точками тест-объекта вдоль оси Z должно составлять от 0,2 до 0,4 расстояния от дальней стены до точки фотографирова- ния (рис. 7.14). При калибровке длиннофокусных (узкоуголь-

рис. 7.13
ных) съемочных камер это отношение выбирается равным 0,4, а корот- кофокусных (широкоугольных) — 0,2. Для решения задачи калибровки необходимо располагать точки тест-объекта не менее чем в двух пло- скостях. Однако для обеспечения возможности калибровки камер с раз- личными фокусными расстояниями и повышения точности калибровки желательно располагать точки тест-объекта в 3–5 плоскостях.
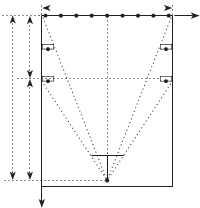 На нулевом уровне марки располагаются по вертикали 6–7 рядами, в каждом из которых по 8–10 марок (см. рис. 7.14). На первом, втором уровнях и последующих уровнях марки располагаются по периферии по 8–10 марок на каждой стене, на потолке и на полу. Точки (марки) тест- объекта должны быть выполнены в виде четких геометрических фигур, обеспечивающих максимальную точность наведения измерительной марки цифровой фотограмметри-
На нулевом уровне марки располагаются по вертикали 6–7 рядами, в каждом из которых по 8–10 марок (см. рис. 7.14). На первом, втором уровнях и последующих уровнях марки располагаются по периферии по 8–10 марок на каждой стене, на потолке и на полу. Точки (марки) тест- объекта должны быть выполнены в виде четких геометрических фигур, обеспечивающих максимальную точность наведения измерительной марки цифровой фотограмметри-
ческой системы при измерении координат их изображений на снимках в интерактивном и ав- томатическом режимах.
Координаты точек тест- объекта должны быть определе- ны в местной прямоугольной си- стеме координат, координатная плоскость XY которой должна быть приблизительно параллель- на плоскости дальней стены, а ось Z — дополнять систему ко- ординат до правой.
∆X X
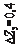 -0 уровень
-0 уровень
-2 уровень
 -1 уровень
-1 уровень
l X
f S
Z
рис. 7.14
Координаты X и Y точек должны быть определены со средними квадратическими погрешностями, максимально допустимые значения
которых определяются по формуле m
X = m Y
= 0,1 Zmin D, где Z
 f
f
min
— рас-
стояние по оси Z от точки фотографирования до ближайшей к ней точки тест-объекта; 0,1 — точность (в пикселях), с которой можно измерить координаты точек снимков в автоматическом режиме; f — фокусное расстояние съемочной камеры; ∆ — размер пикселя светоприемной ма- трицы съемочной камеры. Такая точность координат точек тест-объекта обеспечит точность определения координат главной точки и дисторсии объектива примерно 0,2–0,5 пикселя.
Координаты Z точек должны быть определены со средними ква- дратическими погрешностями, максимальное значение которых, опре- деляется по формуле m Z = ΔZ/20 000, где ∆Z — глубина тест-объекта, т.е. расстояние вдоль оси Z от дальней стены до ближайшей к съемочной камере точки тест-объекта. Такая точность точек тест-объекта обеспечит точность определения фокусного расстояния камеры примерно 1/10000.
Пример: предположим, что камера имеет f = 50 мм, а размер пикселя
∆ = 0,005 мм. Тест-объект имеет следующие размеры: Zmin= 6 м; ∆Z = 2 м. Тогда
m X=m Y=0,06 мм, m Z = 0,1 мм.
Определение пространственных координат точек тест-объекта целесообразно проводить методом прямой геодезической засечки с помощью электронных тахеометров, обеспечивающих измерение го- ризонтальных и вертикальных углов со средними квадратическими погрешностями 3–5².
Определение элементов внутреннего ориентирования съемочных камер, т.е. их фотограмметрическая калибровка по снимкам простран- ственного тест-объекта, основано на совместном решении системы уравнений коллинеарности, составляемых для каждого измеренного на цифровом снимке изображения точки тест-объекта. Эти уравнения имеют вид:
x - f a11 ( X - X S ) + a21 (Y - Y S ) + a31 (Z - Z S ) - x + d

= 0; ü
|
a13
( X - X S
) + a23
(Y - Y S
) + a33
(Z - Z S )
x ï
ï (7.3.2)
a ( X - X ) + a (Y - Y ) + a (Z - Z ) ý
y0 - f
12
a13
S
( X - X S
22
) + a23
S
(Y - Y S
32
) + a33
S
(Z - Z S )
- y + d y
= 0,ï
þ
где f — фокусное расстояние съемочной камеры; x0, y0 — координаты
главной точки в системе координат снимка; x, y — координаты изобра- жения точки тест-объекта в системе координат снимка; X, Y, Z — коорди- наты соответствующей точки тест-объекта в системе координат объекта; X S, Y S, Z S — координаты точки фотографирования (центра проекции); a ij — элементы матрицы преобразования координат (направляющие косинусы), являющиеся функциями угловых элементов внешнего ориен- тирования съемочной камеры ω, α, κ; d x, d y — поправки в измеренные на снимке координаты x, y изображения точки тест-объекта за дисторсию объектива, определяемые уравнениями (7.3.1).
Полученную по всем измеренным на снимке изображениям точек тест-объекта систему уравнений решают способом приближений по ме- тоду наименьших квадратов. в результате решения системы уравнений определяют элементы внешнего ориентирования снимка X S, Y S, Z S, ω, α, κ и элементы внутреннего ориентирования снимка f, x0, y0, k1, k2, k3, p1, p2 с оценкой точности их определения.
При решении исходные уравнения приводят к линейному виду, раскладывая их в ряд Тейлора с сохранением членов только первого порядка малости, и переходят к уравнениям поправок вида:
Bδ + L = V,
(7.3.3)
где B — матрица коэффициентов уравнений поправок (частные произ- водные от исходных уравнений по неизвестным) размерностью m×n (m
— число уравнений, n — число неизвестных); δ — матрица поправок к элементам внешнего ориентирования снимка и элементам внутреннего ориентирования, размерностью 1×n; L — матрица свободных членов размерностью 1×m; V — матрица поправок в измеренные координаты точек снимка размерностью 1×m.
в нашем случае m = 2k, где k — число точек тест-объекта, измерен- ных на снимке, n = 14.
æ a a a ... a a ö
ædX S ö
æ l ö
æ v ö
ç 11 12 13 113 114 ÷
ç dY ÷
ç x1 ÷
ç x1 ÷
ç b11
b12
b13 ... b113
b1 14 ÷
ç S ÷
ç l y1 ÷
ç v y1 ÷
B = ç . . . . . . ÷; δ = ç dZ S ÷; L = ç ... ÷; V = ç ... ÷.
ç ÷ ç ... ÷ ç ÷ ç ÷
ç a k1 a k 2 a k 3 .... a k 13 a k 14 ÷ ç ÷ ç l xk ÷ ç v xk ÷
ç b b b
... b b ÷
ç dp1 ÷
ç l ÷
ç v ÷
è k1 k 2 k 3
k 13 k 14 ø
çç dp ÷÷
è y k ø
è y k ø
è 2 ø
Значения коэффициентов уравнений поправок (7.3.3) a i, b i вычис- ляются по известным значениям координат х, ó изображений точек тест-объекта измеренных на снимке, координат точек тест-объекта X, Y, Z и приближенным значениям элементов внешнего ориентирования снимка X S, Y S, Z S, ω, α, κ и элементов внутреннего ориентирования снимка f, x0, y0, k1, k2, k3, p1, p2. Свободные члены l х, l ó вычисляются по формулам (7.3.2) таким же образом.
Для решения системы линейных уравнений (7.3.3) по методу наи- меньших квадратов переходят к нормальным уравнениям:
BT PBδ + BT PL = 0
или
Nδ + LN = 0,
(7.3.4)
где N — матрица коэффициентов нормальных уравнений размерностью n×n; LN — матрица размерностью 1×n свободных членов нормальных уравнений; P — диагональная матрица весов измерений,
æ p1 0 0 ... 0 ö
|
|
ç p2
P = ç 0 0
0 ... ÷
|
|
p ... 0 ÷; p = 1 ;
3 i m2
|
|
ç ... ... ... ...
è 0 0 0 0
÷ i
÷
p m ø÷
m i — средняя квадратическая ошибка i-го измерения. в результате решения уравнений (7.3.4) получим:
δ = –N–1LN
или
δ = QLN (7.3.5)
где Q — обратная матрица коэффициентов нормальных уравнений.
Таким образом, получают поправки ко всем приближенным значениям неизвестных элементов внешнего ориентирования снимка и элементам внутреннего ориентирования камеры и вычисляют их уточненные значения:
|
X S¢ = X 0 + dX ¢;
|
p2¢ = p0 + dp2¢ .
По уточненным значениям неизвестных снова составляют уравне- ния поправок (7.3.3) и решают полученную систему уравнений по мето- ду наименьших квадратов. Так продолжают до тех пор, пока поправки к неизвестным станут пренебрегаемо малыми величинами. в результате получают уравненные значения элементов внешнего ориентирования снимка и элементы внутреннего ориентирования камеры. в последнем приближении выполняют оценку точности определения неизвестных, т.е. вычисляют средние квадратические ошибки неизвестных:
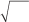 m j =m
m j =m
 m=
m=
Q jj ; (7.3.6)
, (7.3.7)
где μ — средняя квадратическая ошибка единицы веса; Q jj — диагональ- ные элементы обратной матрицы; m–n — число избыточных измерений. С целью повышения надежности и точности определения элементов внутреннего ориентирования калибруемых камер, целесообразно про- изводить съемку тест-объекта многократно с поворотом камеры вокруг оптической оси объектива на 180° и определять искомые параметры в результате совместной обработки измерений, выполненных по всем
полученным снимкам.
|
Критерием оценки точности проведенной фотограмметрической калибровки цифровой камеры и, как следствие, критерием пригодности камеры для выполнения фотограмметрических определений являются значения остаточных погрешностей координат измеренных на снимке точек. Их значения в зависимости от типа калибруемой съемочной ка- меры должны лежать в пределах
от 0,15 до 0,5 пикселя.
По тест-объекту кафедры фотограмметрии МИИГаиК бы- ла выполнена калибровка циф- ровой фотокамеры (рис. 7.15). На рис. 7.16 и 7.17 представлены два образца сертификатов этой кали- бровки. в первом сертификате за единицу измерений был принят пиксель, а во втором миллиметр.
рис. 7.15
СЕРТИФИКАТ КАЛИБРОВКИ ЦИФРОВОЙ ФОТОКАМЕРЫ
Тип камеры – CANON 5D MARK II Серийный номер – 2931522107
Объектив CANON LENS EF – 50 мм
Серийный номер – 14786
Фокусное расстояние
f = 8075,4 +/– 0,4 пикселя
Координаты главной точки:
x0 = 6,4 +/– 0,4 пикселя
y0 = 16,8 +/– 0,6 пикселя
 ó
ó
х
Начало системы координат снимка совмещено с центром матрицы
Параметры радиальной дисторсии:
k1 = –2,1391E–009 +/– 1,4421E–011
k2 = 2,8649E–017 +/– 1,3462E–018
Поправки в координаты измеренных на снимке точек, учитывающие влияние радиальной дисторсии, вычисляют по формулам:
d x = (x − x0 )(r 2k1 + r 4k2 ) ;
d y = ( y − y0 )(r 2k1 + r 4k2 ),
где r =
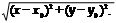
рис. 7.16
СЕРТИФИКАТ КАЛИБРОВКИ ЦИФРОВОЙ ФОТОКАМЕРЫ
Тип камеры – CANON 5D MARK II Серийный номер – 2931522107
Объектив CANON LENS EF – 50 мм
Серийный номер – 14786 Размер пикселя – 6,2 мкм Фокусное расстояние
f = 50,068 +/– 0,002 мм
Координаты главной точки:
x0 = 0,040 +/– 0,003 мм
y0 = 0,104 +/– 0,004 мм
 ó
ó
х
Начало системы координат снимка совмещено с центром матрицы
Параметры радиальной дисторсии:
k1 = –5,5646E−005 +/− 3,7515E−007
k2 = 1,9388E−008 +/− 9,1104E−010
Поправки в координаты измеренных на снимке точек, учитывающие влияние радиальной дисторсии, вычисляют по формулам:
d x = (x − x0 )(r 2k1 + r 4k2 ) ;
d y = ( y − y0 )(r 2k1 + r 4k2 ) ,
где r =
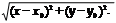
рис. 7.17
К а л и бр о в к а ц и ф р о в ы х ф о т о к а м е р п о с н и м к а м п л о с к о г о т е с т - о б ъ е к т а, представляющего собой поле марки- рованных точек, расположенных в плоскости, имеет свои особенности, связанные с возможной неопределенностью решения задачи в следствии корреляции фокусного расстояния f с отстоянием Z S при решении об- ратной засечки. Это обстоятельство поясняет рис. 7.18.
Предположем, что плоский тест-объект был снят камерой с фокус- ным расстоянием f из точки S, установленной от объекта на отстоянии
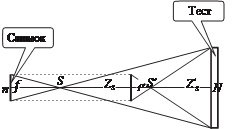 Z S = SN. в результате решения об- ратной засечки при совместном нахождении f и Z S возникает мно- гозначность решения, одним из которых являются произвольные значения f′ и Z′S (см. рис. 7.18), при котором все проектирующие лучи пересекаются в точке S′. в то же время для пространствен-
Z S = SN. в результате решения об- ратной засечки при совместном нахождении f и Z S возникает мно- гозначность решения, одним из которых являются произвольные значения f′ и Z′S (см. рис. 7.18), при котором все проектирующие лучи пересекаются в точке S′. в то же время для пространствен-
рис. 7. 18
ного объекта существует только одно решение в точке S, так как
в точке S′ не пересекаются все лучи (рис. 7.19).
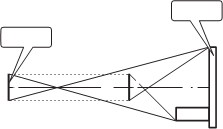
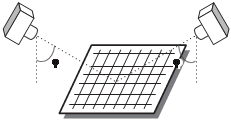
При использовании для фотограмметрической калибровки цифро- вых фотокамер плоского тест-объекта съемку необходимо выполнять при горизонтальном расположении камеры и с наклоном оптической оси камеры относительно плоскости тест-объекта (рис. 7.20), что позволит избежать неопределенности решения задачи. Рекомендуется выполнить наклонную съемку со всех сторон тест-объекта при приблизительно равном угле наклона съемочной камеры.
Снимок
n f S
Z f ' S'
Тест
 Z ' S N
Z ' S N
h
Рис. 7.21 иллюстрирует то обстоятельство, что при съемке плоского тест-объекта с на- клоном оптической оси камеры относительно этого объекта проблема неопределенности решения обратной засечки отсут- ствует, так как существует толь- ко одно решение для точки S (по
|
аналогии с пространственным
рис. 7. 19
тест-объектом (см. рис. 7.19)).
 Определение элементов внутреннего ориентирования камеры по полученным таким образом снимкам производится в результате совместной обра- ботки результатов измерений по всем полученным снимкам, так же, как и при обработке снимков пространственного тест-объекта. Точки (марки) тест-объекта должны быть выполнены в виде четких геометрических фигур, обеспечивающих максимальную
Определение элементов внутреннего ориентирования камеры по полученным таким образом снимкам производится в результате совместной обра- ботки результатов измерений по всем полученным снимкам, так же, как и при обработке снимков пространственного тест-объекта. Точки (марки) тест-объекта должны быть выполнены в виде четких геометрических фигур, обеспечивающих максимальную
точность наведения при измере- n
|
нии их координат тахеометром на объекте и с помощью фото- грамметрической системы на снимках. Наиболее оптималь- ными фигурами для маркирова- ния точек тест-объекта являются окружность и крест. На рис. 7.22 приведен пример плоского тест- объекта, имеющего маркирован- ные точки в виде окружностей (ГОСНИИаС). Причем каждая точка имеет уникальный гра- фический код, позволяющий автоматически определить номер данной точки.

 рис. 7. 20
рис. 7. 20
рис. 7. 21
рис. 7. 22
§7.4. Системы координат и элементы ориентирования наземных снимков
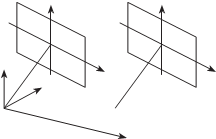
в наземной фотограмметрии используются те же системы ко- ординат снимка, объекта и фотограмметрической модели, которые применяются при обработке аэро- и космических кадровых снимков. Дополнительно в наземной фотограмметрии используют б а з и с н у ю с и с т е м у к о о р д и н а т (рис. 7.23).
 y y
y y
Z x x Y
|
B
1 2
X
рис. 7. 23
Начало базисной системы координат совмещено с центром проекции левого снимка S1. Ось Z совмещена с вертикалью, проведенной из центра проек- ции S1. Ось X совпадает с про- екцией базиса фотографиро- вания на горизонтальную пло- скость XY, проведенную через центр проекции S1. Ось Y до- полняет систему до правой. в качестве элементов внешнего
ориентирования наземных снимков используются те же элементы, что и для аэроснимков. Единственное отличие заключается в значении поперечного угла наклона w, которое для наземных снимков равно примерно 90°. Следует отметить, что в наземной фотограмметрии в от- личии от аэрофотограмметрии углы наклона снимков могут принимать значения от 0 до 360°, в зависимости от решаемой задачи.










