§6.16. ортофототрансформирование изображений, полученных сканерными съемочными системами
Ортофототрансформирование кадровых космических снимков вы- полняется по тем же алгоритмам, что и аэрофотоснимки. При создании ортофотопланов по изображениям, полученным с помощью сканерных съемочных систем, имеются особенности, связанные прежде всего с геоме- трией построения таких изображений. Как известно, у таких изображений каждыйпиксельилистрока(взависимостиоттипа сканернойсистемы) име- ют свои элементы внешнего ориентирования. Поэтому достаточно сложно
d X,Y,Z
Z
М
O
S i m(x,y)
Строка исходного изображения
Цифровая модель рельефа
X
реализовать обратное трансфор- мирование из-за невозможности установить однозначное соответ- ствие между точками местности и сканерного изображения. Ортофо- тотрансформирование сканерных изображений можно выполнить с помощью прямого трансформи- рования по известным элементам внешнего ориентирования каждой
X , Y
O
Y
рис. 6.36
Ортофотоплан
X
строки или точки или с помощью обратного трансформирования, используя RPC-коэффициенты. Рассмотрим каждый из этих ва- риантов ортофототрансформиро- вания.
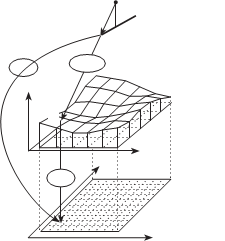
П р я м о е т р а н с ф о р м и р о в а н и е. Суть метода заключается в следующем. Предположим, что для каждого пикселя m(x, y) сканерного изображения известны элементы внешнего ориентирования (рис. 6.36). Тогда можно найти координаты X, Y, Z соответствующей точки местности М как точки пересечения вектора S im с цифровой моделью рельефа. Затем в пиксель ортофотоизображения с координатами X, Y переносится яркость пикселя исходного изображения d (см. рис. 6.36). Таким образом поступают с каждым пикселем сканерного изображения. в результате получают ортофотоплан на заданный участок местности. Определение координат X, Y, Z точки местности М производится методом приближений, следующим образом. Сначала вычисляются значения координат X, Y в системе координат цифрового ортофотоплана
по формулам
X = X
+ (Z - Z
) X ¢ ;
é X ¢ù é x - x0 ù
|
Z ¢ ê Y ¢ ú = ê - ú
Y ¢ ê ú
A êy y0 ú
(6.16.1)
Y = Y S + (Z - Z S ) Z ¢ ; êë Z ¢ úû
или по формулам
ê -f úû
X = R1(x, y, Z ) ;
R2 (x, y, Z )
Y = R3 (x, y, Z ) . (6.16.2)
R4 (x, y, Z )
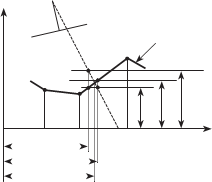
в первом приближении значение высоты узла принимают рав- ной среднему значению высот точек цифровой модели рельефа Z1 (рис. 6.37). По вычисленным
значениям X1, Y1 по цифровой Z
модели рельефа методом би-
|
линейной интерполяции опре- деляют уточненное значение высоты точки Z2, по которому определяют уточненное значе- ние координат точки X2,Y2. По координатам X ,Y , в свою оче-
S
f P Цифровая модель
O рельефа
|
|
Z 3 Z1
редь, определя
2 2
т овое значение O
ю н X1
высоты точки Z3. вычисление продолжают до тех пор, пока разность значений координат
X2
X3
рис. 6.37
X и Y точки в приближениях не будут превышать установленного до- пуска. возможен вариант, в котором контролируется разность высот точек в приближениях.
Прямое трансформирование имеет некоторые недостатки, а именно этот метод требует больших затрат машинного времени из-за итерацион- ного процесса нахождения координат точки местности М, соответствую- щей точке сканерного изображения m. Кроме того, в этом случае могут получиться разрывы в изображении ортофотоплана.
О б р а т н о е т р а н с ф о р м и р о в а н и е. Суть обратного транс- формирования заключается в следующем. Задаваясь координатами X, Y какого-либо пикселя на ортофотоплане, по цифровой модели рельефа определяют координату Z точки местности М (см. рис. 6.36) Затем по известным элементам внутреннего и внешнего ориентирования сним- ка и координатам точки местности М по уравнениям коллинеарности вычисляют координаты x, y, соответствующей точки m на исходном снимке по которым берется яркость d и переносится на ортофотоплан. Реализация данного принципа трансформирования для сканерных изо- бражений проблематична, так как неизвестно в какой момент времени было сформировано изображение точки местности М, а следовательно, непонятно на какой строке сканерного изображения находится данное изображение, т.е. элементы внешнего ориентирования какой строки сканерного изображения следует использовать для данной точки. По- этому задача обратного трансформирования реализуется в полной мере только при наличии RPC-коэффициентов. в этом случае, после нахож- дения координаты Z точки М местности по цифровой модели рельефа вычисляют координаты x,y точки m сканерного изображения, используя уравнения (6.5.7). Затем, по полученным координатам берется яркость изображения d и переносится на ортофотоснимок.
|
в настоящее время большинство поставщиков сканерных космиче- ских изображений поставляют эти изображения вместе со значениями RPC-коэффициентов. Если на данный участок местности имеются еще и опорные точки, то возможно уточнение значений RPC- коэффициентов в современных фотограмметрических системах. Это позволяет несколько повысить точность построения ортофотоплана по таким изображениям.
 |
Глава 7
 |