Тождества. Тождественные преобразования выражений
Второе ноября
Классная работа
Тождества. Тождественные преобразования выражений
№ 1 Найдем значения выражений
3(х+у) и 3х+3у
1) при х=5 и у=4:
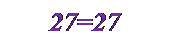3(х+у)=3(5+4)=3•9= 27,
3х+3у=3•5+3•4= 27;
2) при х=6 и у=5:
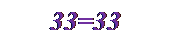3(х+у)=3(6+5)=3•11= 33,
3х+3у=3•6+3•5= 33.
В обоих случаях мы получили одинаковые результаты.
Из распределительного свойства следует, что вообще при любых значениях переменных значения выражений 3(х+у) и 3х+3у будут равны.
3(х+у) = 3х+3у
№ 2 Найдем значения выражений
2х+у и 2ху
1) при х=1, у=2 :
2х+у=2 • 1+2= 4,
2ху=2 • 1 • 2= 4
выражения принимают равные значения
2) при х=3, у=4 :
2х+у=2 • 3+4= 10,
2ху=2 • 3 • 4= 24
значения выражений не равны.
Говорят, что выражения 3(х+у) и 3х+3у являются тождественно равными, а выражения 2х+у и 2ху не являются тождественно равными.
Таким образом, равенство 3(х+у) = 3х+3у верно при любых значениях х и у. Такие равенства называются тождествами.
С тождествами мы уже встречались. Так, тождествами являются равенства, выражающие основные свойства действий над числами.
Примеры тождеств
a + b = b + a –переместительное свойство сложения
ab = ba –переместительное свойство умножения
(a + b ) + c = a + ( b + c ) –сочетательное свойство сложения
(ab ) c = a ( bc ) –сочетательное свойство умножения
a ( b + c ) = ab + ac –распределительное свойство умножения относительно сложения
а + 0 = а
а • 1 = а
а • 0 = 0
а : а=1
а + (-а) = 0
а • (- b ) = - ab
а- b = a + (- b )
(- a ) • (- b ) = ab
 |
Выполним тождественные преобразования выражений, руководствуясь свойствами действий над числами
№ 90 (б, г)
Упростите выражение, используя переместительное и сочетательное свойства умножения:
б) 4с • (-1,25)= 4 • (-1,25)•с =5с
г) -0,1 b • (-2,3с)= -0,1•(-2,3)• b •с=0,23 b с
№ 93 (б, г)
Замените выражение тождественно равным, используя распределительное свойство умножения:
|
г) -0,1 • (100а + 10b - с)= -10а – b + 0,1c