§6.10. методы получения стереопар радиолокационных изображений
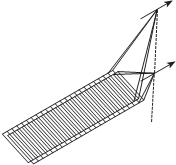
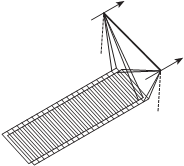
На рис. 6.24 показан традиционный метод получения стереопар радиолокационных изображений съемки с двух параллельных марш- рутов, а на рис. 6.25 – с двух разновысотных маршрутов (базис съем- ки В располагается вертикально). в первом случае (см. рис. 6.24) базис
 Направление Направление
Направление Направление
 S полета
S полета
H B
Направление
S2 полета
H2 B
полета
Направление
S S1
H
H1
полета
рис. 6.24 рис. 6.25
съемки В располагается горизонтально. Съемку с вертикального базиса удобно применять в случае, когда полеты над изучаемой территорией небезопасны, например, над территорией противника.
§6.11. определение координат точек объекта
по одиночному радиолокационному изображению
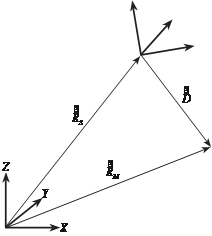
Положение точки местности М в системе координат объекта OXYZ
определяет вектор R M
. вектор D
определяет положение той же точки
относительно начала системы координат радиолокационной системы
Sx yz. вектор R S задает начало системы координат радиолокационной
системы Sx yz в системе координат объекта. Нужно определить коор- динаты точки М.
Из рис. 6.26 следует, что
или в координатной форме
R M = R S + D
(6.11.1)
æ X ö æ X S ö æ D X ö
çY ÷ = çY S ÷ + ç D Y ÷. (6.11.2)
ç ÷ ç ÷ ç ÷
ç Z ÷ ç Z ÷ ç D ÷
è ø è S ø è Z ø
 Здесь D X,D Y, D Z — координаты
Здесь D X,D Y, D Z — координаты
 вектора D в системе координат
вектора D в системе координат

 объекта. Эти координаты можно выразить через соответству- ющие координаты в системе координат радиолокационной системы:
объекта. Эти координаты можно выразить через соответству- ющие координаты в системе координат радиолокационной системы:
æ D X ö æ x ö
M ç D Y ÷ = A ç y ÷. (6.11.3)
ç ÷ ç ÷
çè D Z ÷ø
çè z ÷ø
O
рис. 6.26
Для определения коорди- нат x,y,z в системе координат радиолокационной системы вос- пользуемся рис. 6.27, из которого
следует, что
z
 æ x ö æ 0 ö
æ x ö æ 0 ö
ç y ÷ = D ç
sin j ÷,
(6.11.4)
ç ÷ ç ÷
çè z ÷ø
çè - cos j÷ø S
где D — наклонная дальность (берется со снимка).
Подставляя (6.11.3) и (6.11.4) в (6.11.2)
получим: M
X = X S + (a12 sin j - a13 cosj) D; z
Y = Y S + (a22 sin j - a23 cosj) D; Z = Z S + (a32 sin j - a33 cosj) D.
(6.11.5)
Элементы внешнего ориентирования радиолокационной системы известны из бортовых измерений. Неизвестным является
рис. 6.27
угол φ, который можно найти из третьего уравнения выражения (6.11.5) при условии, что высота точки Z известна.
Так как это уравнение нелинейно, то переходят к линейному урав- нению поправок
aδφ = l X, (6.11.6)
в результате решения которого находят угол φ.
Угол φ можно также найти, если известна высота фотографирова- ния относительно определяемой точки H = Z S – Z. Тогда, как следует из рис. 6.28,
cos j= H .
D
S
 (6.11.7)
(6.11.7)
Определив угол φ, вычис- φ D
ляют координаты X и Y точки H
М по первым двум уравнениям
выражений (6.11.5).
M
рис. 6.28
§6.12. определение координат точек объекта
по стереопаре радиолокационных изображений
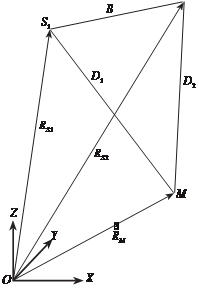 S2 Предположим, что точка местности М изобразилась на паре радиолокационных изо- бражений, полученных в момент S1 и S2 (рис. 6.29), следовательно, известны наклонные дальности D1 и D2. Необходимо найти ко- ординаты вектора R M.
S2 Предположим, что точка местности М изобразилась на паре радиолокационных изо- бражений, полученных в момент S1 и S2 (рис. 6.29), следовательно, известны наклонные дальности D1 и D2. Необходимо найти ко- ординаты вектора R M.
Из рис. 6.29 следует, что
R M = R Si + D i , i=1,2 (6.12.1)
или в координатной форме
æ X ö
æ X Si ö
æ D Xi ö
ç Y ÷ = ç Y ÷ + ç D
÷. (6.12.2)
ç ÷ ç Si ÷
ç Yi ÷
çè Z ÷ø
çè Z Si ÷ø
çè D Zi ÷ø
рис. 6.29
Подставляя в (6.12.2) значе- ния D Xi, D Yi, D Zi из (6.11.3) полу- чим
æ X ö
æ X Si ö
æ 0 ö
ç Y ÷ = ç Y Si ÷ + D i Ai ç sin ji ÷. .(6.12.3)
ç ÷ ç ÷ ç ÷
çè Z ÷ø
çè Z Si ÷ø
çè - cos ji ÷ø
Здесь неизвестными являются углы проектирования φ1, φ2. Чтобы их найти воспользуемся соотношением, которое следует из рис. 6.29:
B = D1 - D2 (6.12.4)
или в координатной форме
æ B X ö æ 0 ö
æ 0 ö
ç B Y ÷ = D1A1 ç sin j1 ÷ - D2A2 ç sin j2 ÷. (6.12.5)
ç ÷ ç ÷ ç ÷
çè B Z ÷ø
çè - cos j1 ÷ø
çè - cos j2 ÷ø
Из уравнений (6.12.5) найдем φ1 и φ2, составив систему уравнений поправок вида:
a1dj1 + a2dj2 + l X = v X ;ü
b dj + b dj + l = v ; ï
(6.12.6)
1 1 2 2 Y Y ý
|
c1dj1 + c2dj2 + l Z = v Z . ï
в этой системе три уравнения с двумя неизвестными. Задача ре- шается по методу наименьших квадратов способом последовательных приближений. После нахождения углов φ1 и φ2 вычисляют координаты точки М по формулам (6.12.3). аналогично поступают со всеми осталь- ными точками.








