§6.5. математическая модель сканерных изображений
Под математической моделью сканерных изображений будем понимать связь координат точек изображений и соответствующих ко- ординат точек местности. Эта связь может быть выражена в виде стро- гих математических зависимостей (с т р о г а я м а т е м а т и ч е с к а я м о д е л ь) или в виде приближенных математических зависимостей (п р и б л и ж е н на я ма т е ма т и ч е с к а я м о д е л ь) Рассмотрим каждую их них.
строгая математическая модель сканерных изображений
Эта модель выражается в виде известных уравнений коллинеар- ности:
прямые формулы
X = X
+ (Z - Z
) X ¢ ;ü

æ X ¢ö æ x ö
Si Si
Z ¢ ï ç ¢ ÷ = ç ÷
Y ¢ ý ãäå çY ÷
Ai ç y ÷;
(6.5.1)
Y = Y Si + (Z - Z Si ) ,

ï ç Z ¢ ÷ ç z ÷
обратные формулы
Z ¢ ïþ
è ø è ø
X * ü æ X * ö

æ X - X ö
|
|
|
x = z ; Si
Z ï ç
ý ãäå çY * ÷ = AT çY - Y ÷.
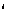
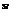
(6.5.2)
Y * ï ç ÷ ç ÷
 |
y = z
Z * , þ
è Z * ø
è Z - Z Si ø
Здесь x, y, z — координаты единичного вектора, определяющие направ- ление на точку сканерного изображения (6.2.2), (6.3.1), (6.4.2), (6.4.3); X,Y,Z — координаты соответствующей точки местности; X Si, Y Si, Z Si — значения линейных элементов внешнего ориентирования съемочной системы в момент формирования изображения i строки или точки изо- бражения; Ai, ωi, αi, κi — матрица поворота и соответствующие ей углы наклона и поворота системы координат сканера в момент формирования i строки или точки изображения.
По координате xс (абсцисса в системе координат сканерного изо- бражения) определяем время формирования изображения i строки изо- бражения, а следовательно, элементы внешнего ориентирования сканера во время формирования изображения этой строки. Уравнения (6.5.1) и (6.5.2) применяются для обработки сканерных изображений в случае, когда известны элементы внешнего ориентирования сканера во время формирования изображения.
приближенная математическая модель сканерных изображений
Применяется в случае обработки последних, когда элементы внеш- него ориентирования сканера неизвестны. в этом случае применяют различные функции для описания закона изменения элементов внешнего ориентирования сканера во время формирования изображения.
1. а п п р о к с и м а ц и я э л ем ен т о в в н еш н ег о о р и - е н т и р ов а н и я ( Э в О ) р а з ли чн ыми п о л ин о м а м и. Связь координат точек сканерного изображения и местности может быть представлена известными уравнениями коллинеарности (6.5.1), (6.5.2), в которых:
X Si = X S 0 + k1Dt i ;
Y Si = Y S 0 + k2Dt i ; Z Si = Z S 0 + k3Dt i ;
w = w + k Dt ; a = a + k Dt ; k = k
+ k Dt ,
(6.5.3)
i 0 4 i i
0 5 i
i 0 6 i
где X S0, …, κ0 — значения элементов внешнего ориентирования сканера в момент формирования первой строки снимка; k1, …, k6 — коэффициенты, характеризующие закон изменения элементов внешнего ориентирования сканера во времени
Dt i = t i - t0 , (6.5.4)
где t i — время получения i-й строки изображения; t0 — время получения первой строки изображения. Эти величины определяются по измере- ниям xc точек на сканерном изображении.
Уравнения (6.5.3) характеризуют линейный закон изменения эле-
ментов внешнего ориентирования сканера в зависимости от времени. возможна другая модель изменения ЭвО сканера, например, полином второй степени:
|
X Si = X So + k1Dt i + d1Dt 2 ;
.........................................
|
k i = kSo + k6Dt i +d6Dt 2.
(6.5.5)
Коэффициенты d будут описывать ускорение изменения ЭвО сканера. Значения элементов внешнего ориентирования сканера в момент формирования изображения начальной строки и закон изменения этих элементов во времени можно определить в результате решения обратной фотограмметрической засечки по опорным точкам. Каждая опорная точка дает возможность составить два уровня (6.5.2) с учетом (6.5.3). Для определения неизвестных значений ЭвО сканера в момент формирования первой строки X S0, …, κ0 и коэффициентов k1, …, k6 не- обходимо измерить минимум шесть опорных точек для составления 12 уравнений. Если еще необходимо определить d i (ускорение), то не-
обходимо 9 опорных точек.
При решении обратной за- сечки по сканерному изображе- нию для равнинной местности возникает неопределенность (множественность) решения задачи определения элементов внешнего ориентирования ска- нера. Как видно из рис. 6.14 для различных положений сканера в пространстве X S0, X Si лучи, про- ходящие через центр проекции
 рис. 6.14
рис. 6.14
и точки снимка, проходят через соответствующие точки на местности. Для избегания этого эффекта следует зафиксировать один из элементов
— X S0, Z S0 или α0. При космической съемке лучше зафиксировать высоту фотографирования Z S0.
2. Св я з ь к о ор д и на т т о ч е к м е с т н о с т и и с к а н е р -
н о г о и з о бр а ж е н и я , в ы р а ж е н на я ч е р е з д р о б н о - р а - ци о н а л ь н ы е ф у нк ции (RPC - к о э ф ф ици е н т ы). в последнее время широкое распространение получили так называемые RPC (rational polynomial coefficients) коэффициенты, которые входят в дробно-раци- ональные функции, описывающие связь координат точек местности и сканерного изображения. Эти функции имеют следующий вид:
прямые функции
 X = R1(x, y, Z ) ;
X = R1(x, y, Z ) ;
R2 (x, y, Z )
Y = R3 (x, y, Z ) ;
 R4 (x, y, Z )
R4 (x, y, Z )
(6.5.6)
обратные функции
 x = P1( X ,Y , Z ) ;
x = P1( X ,Y , Z ) ;
P2 ( X ,Y , Z )
y = P3 ( X ,Y , Z ) ,
 P4 ( X ,Y , Z )
P4 ( X ,Y , Z )
(6.5.7)
где x, y — координаты точек сканерного изображения; X,Y,Z — коорди- наты соответствующих точек местности; R1(x, y, Z), R2(x, y, Z), R3(x, y, Z), R4(x, y, Z), P1(X, Y, Z), P2(X, Y, Z), P3(X, Y, Z), P4(X, Y, Z) — полиномы, имею-
щие, например, следующий вид
R(x, y, Z ) = b0 + b1x + b2y + b3Z + b4 x2 + b5 x y +
+ b6y2Z + b7yZ 2 + b8Z 3 + b9 x2Z ;
(6.5.8)
P( X ,Y , Z ) = a0 + a1 X + a2Y + a3Z + a4 X 2 + a5 XY +
+ a6Y 2Z + a7YZ 2 + a8Z 3 + a9 X 2Z.
(6.5.9)
Коэффициенты a i, b i, входящие в уравнения (6.5.9), называются RPC-коэффициентами и поставляются с космическими сканерными изображениями вместо элементов внешнего ориентирования сканера во время получения изображения.
Рассмотрим процесс получения RPC-коэффициентов на примере изображений, полученных оптико-электронным сканером. При этом полагаем, что элементы внутреннего и внешнего ориентирования ска- нера известны.
На первом этапе устанавливают однозначное соответствие между пикселями сканерного изображения и пространством объекта. Для этого сначала восстанавливают связки проектирующих лучей по эле- ментам внутреннего ориентирования сканера и координатам x, y пик- селей сканерного изображения (рис. 6.15). Теперь, если сориентировать каждую связку проектирующих лучей строки по элементам внешнего ориентирования сканера в момент формирования этой строки S i, то проектирующие лучи пройдут, как известно, через соответствующие точки местности. Координаты точек местности можно вычислить по
(6.5.1), если известны соответствующие высоты Z этих точек. Задаваясь высотами некоторых плоскостей Z1, Z2, Z3, …, можно вычислить коор- динаты X, Y, Z i (i=1,2,3,…) точек пересечения проектирующих лучей с этими плоскостями. в результате будем иметь набор точек местности с координатами X, Y, Z i, каждой из которых соответствует точка на ска-
|
нерном изображении с координа-
S i S j
тами x, y. Количество плоскостей с известными отметками можно
(x, y)
(x, y)
(x, y)
(x, y)
задать произвольно. Например, взять три плоскости с отмет- ками, равными минимальной, максимальной и средней высоте
|
(X,Y, Z3) (X,Y, Z3)
3
(X,Y, Z2) Z2
(X,Y, Z1) Z1
рис. 6.15
на данном участке местности. Таким образом, можно получить для каждого пикселя сканерного изображения (координаты x, y) по три точки в пространстве
объекта (координаты X, Y, Z). Конечно такое огромное количество со- ответствующих точек изображения и местности никто не вычисляет, а задают некоторую регулярную сетку в плоскости изображения (напри- мер, каждый сотый пиксель вдоль оси x и вдоль оси y) и для каждого узла этой сетки вычисляют по три точки в пространстве объекта. Теперь достаточно составить уравнения (6.5.6) или (6.5.7) для каждой пары со- ответствующих точек изображения (x, y) и местности (X, Y, Z) и решить их относительно RPC-коэффициентов методом наименьших квадратов. Если элементы внешнего ориентирования сканера во время фор- мирования изображения неизвестны, то RPC-коэффициенты можно найти по опорным точкам c известными координатами X, Y, Z. Для этого необходимо опознать опорные точки на изображении и измерить их координаты x, y. Затем составляют уравнения (6.5.6) или (6.5.7) для каждой опорной точки и находят RPC-коэффициенты в результате решения системы уравнений (6.5.6) или (6.5.7). Недостаток такого под- хода — необходимость иметь большое количество опорных точек, рас- пределенных по всему диапазону изменения высот местности. Мини- мальное количество опорных точек составляет 20 (одна опорная точка позволяет составить два уравнения (6.5.6) или (6.5.7) с 40 неизвестными
RPC-коэффициентами).
К достоинствам данного метода аппроксимации математической модели сканерных изображений можно отнести следующее:
достаточно точные результаты обработки сканерных изображений, соизмеримые с разрешающей способностью изображений;
универсальность метода, он подходит для всех типов сенсоров.
3. С в я з ь к о о р д и н а т т о ч е к м е с т н о с т и и с к а н е р н о - г о и з о б р а ж е н и я , в ы р а ж е н на я ч е р е з а п п р о к с и м и р у - ю щи е ф у нк ци и. в качестве аппроксимирующих функций могут быть использованы различные функции, например:
п р о е к т и в н а я м о д е л ь (иначе ее называют Direct Linear Transformation — DLT)
x = A1 X + A2Y + A3Z + A4 ; y = B1 X + B2Y + B3Z + B4 , (6.5.10)


C1 X + C2Y + C3Z + 1 C1 X + C2Y + C3Z + 1
здесь в качестве неизвестных выступают 11 коэффициентов, для нахождения которых необходимо иметь минимум шесть опорных точек;
а ф ф и н на я м о д е л ь
x = A1 X + A2Y + A3Z + A4 ;
y = B1 X + B2Y + B3Z + B4 ,
(6.5.11)
в этом случае необходимо иметь минимум четыре опорные точки для нахождения восьми неизвестных коэффициентов;
па р а л л е л ь н о - п е р с п е к т и в на я м о д е л ь
 x = L1 X + L2Y + L3Z + L4 ;
x = L1 X + L2Y + L3Z + L4 ;
L5 X + L6Y + L7Z + 1
y = L8 X + L9Y + L10Z + L11,
(6.5.12)
необходимо иметь минимум шесть опорных точек для нахождения 11 неизвестных коэффициентов.
Как показали многочисленные эксперименты из всех приближен- ных методов описания математической модели сканерных изображений наиболее адекватно описывают первые два метода: метод, основанный на вычислении закона изменения элементов внешнего ориентирова- ния сканера во времени формирования изображения и метод RPC- коэффициентов. Как следствие они дают наиболее точные результаты обработки сканерных изображений.









