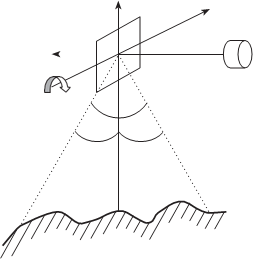
§6.3. принцип формирования изображения с помощью оптико-механической сканерной съемочной системы. системы координат сканера
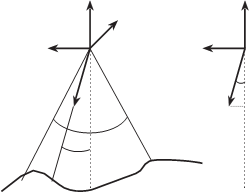
Изображение строки в оптико-механическом сканере формируется за счет вращения зеркала, а строки — за счет перемещения носителя съемочной системы. Таким образом, каждый пиксель изображения имеет свои элементы внешнего ориентирования: θ — угол поля зрения сканера, началом системы координат сканера является точка S — точка пересечения оси вращения зеркала и главной оптической оси объектива; ось x совпадает с осью вращения зеркала; ось z — с биссектрисой угла поля зрения съемочной системы; ось y дополняет систему до правой (рис. 6.8).
Система координат сканерного изображения задается так же как и для оптико-электронного сканера, т.е. ось yс совпадает c одной из строк изображения, начало системы координат О находится в середине строки, а ось xс дополняет систему до правой (рис. 6.9). По измеренным коорди- натам точки изображения xс, yс можно получить время формирования изображения данного пикселя, а следовательно, и элементы внешнего ориентирования сканера в этот момент.
z
 x
x
 Зеркало
Зеркало
 S
S
y
Объектив Фотоприемник
θ Диафрагма
θ θ
2 2
 z z
z z
x
y S y S
xc r z
r φ
m m y
θ
φ
M
рис. 6.9
Направление на точку местности М (см. рис. 6.9) в системе коор- динат сканера определяет единичный вектор r, координаты которого можно определить следующим образом:
æ 0 ö
æ 0 ö
q
r = ç sin j ÷ = ç y ÷; j =
y m ,
(6.3.1)
ç ÷ ç ÷ l
çè - cos j÷ø
çè z ÷ø y
где l y — размер кадра в пикселях вдоль оси y; y m — координата точки
m в системе координат изображения.
все дальнейшие рассуждения и определение координат точек местности по сканерным изображениям будут одинаковыми для опти- ко-механического и оптико-электронного сканеров.
§6.4. методы получения стереопар сканерных изображений
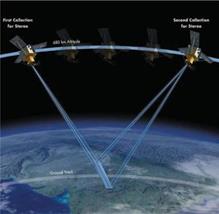
Существует два основных метода получения стереопар сканерных изображений: со смежных орбит и с одной орбиты (в аэросъемке марш- рут эквивалентен орбите).
См е ж н ы е ор б и т ы (рис. 6.10).
Недостаток: нельзя точно выбрать базис, одну и ту же территорию снимают в разное время (различные освещенность, тени и т.д.).
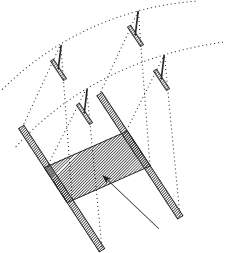
О д н а о р б и т а — о д н а к а м е р а наклоняется сначала на угол α1, а затем на угол α2. Задавая различные углы наклона камеры
|
Орбита 1
i
S1 Орбита 2
S j
S2
можно выбрать длину базиса B
(рис. 6.11).
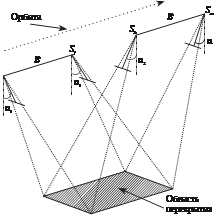
О д на о р б и т а — т р и к а м е р ы с наклоном оптиче- ских осей относительно друг друга на угол α, при этом одна камера смотрит в надир. в ре- зультате имеем три стереопары (рис. 6.12). У каждой камеры должно быть свое фокусное рас- стояние с тем, чтобы масштабы изображений были одинаковы- ми:
Область перекрытия
1 = f0
 m D0
m D0
. (6.4.1)
рис. 6.10
Очевидно, что D
= D0 ,
 cos a
cos a
тогда для сохранения масштаба должно быть
fí =
f0 .
 cos a
cos a
аналогично
 для камеры, которая направлена вперед fï
для камеры, которая направлена вперед fï
= f0 . cos a
|
2
S i
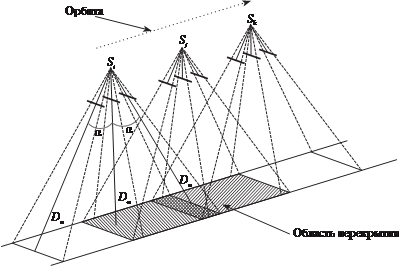
рис. 6.12
О д на к а м е р а с т р е м я л и н ей к а м и. Для получения стереоскопических сканерных изображений в фокальной плоскости объектива сканерной съемочной системы располагают не одну а три или более линейки ПЗС, формирующих изображение одного и того же участка местности под разными углами (рис. 6.13).
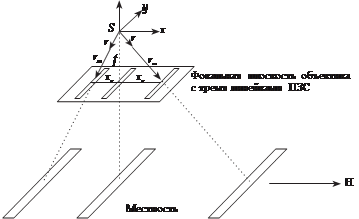 z
z
аправление полета
рис. 6.13
величины xн, xп являются постоянными величинами для камеры и определяются в результате ее калибровки. Координаты единичного вектора r, определяющего направление на точку местности в системе координат сканера, в зависимости от расположения линейки ПЗС будут вычисляться по следующим формулам:
æ xí - x0 ö
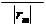 ç ÷
ç ÷
ç ÷ æ x ö
 |
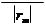 ç y - y ÷ ç ÷
ç y - y ÷ ç ÷
r = ç ÷ = ç y ÷,
ç ÷ ç z ÷
(6.4.2)
ç -f ÷ è ø


|
|
ç ÷

 где
где
r m =
ç r m ÷
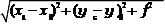 ;
;
æ xï - x0 ö
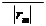 ç ÷
ç ÷
|
ç ÷ æ x ö
r = c 0 = ç y ÷,
(6.4.3)
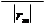 ç ÷ ç ÷
ç ÷ ç ÷
ç ÷ ç z ÷
ç -f ÷ è ø
ç ÷


|
|
ç r m ÷


 где r = (x - x )2 + (y - y )2 + f2 .
где r = (x - x )2 + (y - y )2 + f2 .
m ï 0 c 0