§5.10. Автоматическое построение плотного облака точек по паре снимков на основе полуглобального метода отождествления соответственных точек
в последнее время широкое распространение получили методы, позволяющие строить плотные облака точек по стереопаре снимков. Причем точки облака определяются для всех соответственных пик- селей стереопары. в основе этих методов лежит идентификация всех пикселей левого снимка стереопары с соответствующими пикселями правого снимка. Это можно сделать с помощью различных методов, которые составляют три большие группы: локальные, глобальные и полуглобальные методы.
К л о к а ль ным м е т о д а м о т о ж д е с тв л е ни я относятся все площадные методы отождествления (корреляционный, метод наимень- ших квадратов и их модификации), основанные на сравнении фрагментов изображений двух снимков вокруг интересующей точки, исходя из предпо- ложения, что продольные параллаксы для всех пикселей этих фрагментов не меняются. Такие методы не очень хорошо работают на участках снимков со слабовыраженной текстурой и на границах объектов с большим пере- падом высот (края крыш зданий и т.д.).
М е т о д ы гло б а л ь н о г о о т о ж де с т в л е н и я основаны на нахождении оптимального отождествления сразу для всех пикселей стереопары снимков. в этой группе методов анализируются не только разности яркостей соответствующих пикселей, но и взаимосвязи между соседними пикселями на предмет изменения разностей продольных па- раллаксов, что позволяет более точно (по сравнению с локальными мето- дами) определить продольные параллаксы для всех пикселей стереопары. Недостаток этой группы методов — большие затраты машинного времени. Наиболее распространенным в настоящее время алгоритмом построения плотного облака точек по стереопаре снимков является так называемое п о л у гл о б а л ь н о е о т о ж де с т в ле н ие (Semi- GlobalMatching (SGM)) — метод, предложенный Хиршмюллером. Рас-
смотрим более подробно данный метод.
|
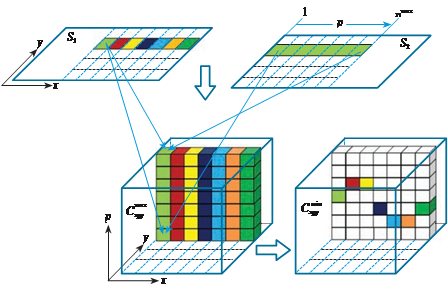
Суть метода заключается в том, чтобы каждому пикселю левого снимка стереопары S1 (рис. 5.25) был найден соответствующий пиксель на правом снимке S2. Метод рассчитан на применение трансформирован- ных снимков, т.е. все соответствующие точки находятся вдоль базисных (эпиполярных) линий. Каждый пиксель левого снимка сравнивается со всеми пикселями второго снимка в пределах возможного изменения про- дольных параллаксов pmax и каждый раз вычисляется «стоимость» C x p отождествления. Эта стоимость чаще всего вычисляется как разность соответствующих яркостей пикселей:
C x p = D1 - D2 , (5.10.1)
y xy py
где D1 , D2
— яркости пикселей соответственно первого и второго
xy py
снимков стереопары; p — продольный параллакс, p=x1–x2.
По (5.10.1) вычисляется стоимость для каждого пикселя левого снимка с координатами x, y и всех пикселей, лежащих в строке с орди- натой y на правом снимке и в пределах возможных продольных парал- лаксов p=1÷pmax, а результат заносится в соответствующую ячейку куба с координатами x, y, p (см. рис. 5.25, a). Таким образом, формируется куб стоимостей отождествления каждого пикселя на левом снимке с
 |
а б
рис. 5.25
возможными пикселями на правом. анализируя эти стоимости нахо- дят минимальные значения для каждого пикселя (см. рис. 5.25, б), так как чем меньше стоимость, тем больше вероятность того, что пиксели являются соответствующими (тот же принцип, что и в локальных мето- дах отождествления). в результате имеем для каждого пикселя левого снимка соответствующее значение продольного параллакса. Решение, показанное на рис. 5.25, б, является только первым приближением, так как основано на сравнении яркостей между пикселями и не учитывает связей между ними.
На втором этапе анализируются параллаксы соседних пикселей по восьми направлениям, и стоимость отождествления пикселей увеличи- вается в зависимости от величины разности продольных параллаксов. в общем виде задачу полуглобального отождествления можно записать в виде некоторого функционала, зависящего от параллаксов:
 E ( p) = åìC + åP éë p - p
E ( p) = åìC + åP éë p - p
= 1ùû + åP éë p - p > 1ûùü. (5.10.2)


 í xyp 1 q
í xyp 1 q
î
2 q ý
þ
Здесь C — функция стоимости отождествления точки с координата- ми x, y на левом снимке и точки с координатами x–p, y на правом снимке. второе слагаемое добавляет «штраф» P1=1 в значение стоимости С для текущего параллакса р, если разность параллаксов р и p q (продольный параллакс соседнего пикселя) равна единице, в остальных случаях P1=0. Третье слагаемое добавляет к стоимости отождествления С штраф P2, если разность параллаксов соседних пикселей больше единицы.
Глобальные методы отождествления минимизируют функционал (5.10.2) в двумерном пространстве, анализируя все связи каждого пикселя изображения, что очень трудоемко. Поэтому в полуглобальном методе анализ связей пикселей выполняется по независимым одномерным на- правлениям, что позволяет осуществить достаточно быстрые алгоритмы минимизации функционала (5.10.2). Обычно используют 8 направлений вокруг данного пикселя.
Добавление стоимости по каждому из восьми направлений L r
(рис. 5.26) можно выполнить независимо на основе рекурсивной формулы
L r ( x, y, p) = C ( x, y, p) + min{L r ( x r , y r , p), L r ( x r , y r , p -1) +
|
+ P1, L r ( x r , y r , p + 1) + P1, min L r ( x r , y r ,i) + P2}- (5.10.3)
-
|
min L r ( x r , y r , k ),
рис. 5.26
где x, y — координаты рассма- триваемого пикселя; р — зна- чение параллакса, для которого выполняется вычисление стои- мости отождествления; x r=x–r; y r=y–r; направления r задаются путем смещения к одному из восьми пикселей соседних с данным, т.е. r1=(1, 0), r2=(1, 1), …, r8=(1, –1).

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Минимизация по i и k вы-
полняется по выбранному диапа-
зону рассматриваемых параллаксов. Первый член в (5.10.3) представляет собой стоимость отождествления пикселей для данного параллакса, второй — стоимость оптимального предшествующего отождествления с добавлением штрафа, а третье слагаемое добавляется для предотвраще- ния излишнего роста функции стоимости. Третье слагаемое не влияет на выбор оптимальных значений.
Финальное значение (сглаженное) стоимости для каждого пикселя и каждого параллакса S(x, y, p) получается путем суммирования стои- мостей L r(x, y, p) по всем направлениям r:
S ( x, y, p) = åL r (x, y, p).
r
(5.10.4)
|
рис. 5.27
На заключительном этапе, анализируя S(x, y, p), находят для каждого пикселя с координатами x, y соответствующий парал- лакс р, для которого стоимость S минимальна. Затем достаточно решить прямые фотограмметри- ческие засечки для каждого пик- селя, чтобы получить 3D-модель объекта в виде плотного облака точек. На рис. 5.27 показан при- мер плотного облака точек,
построенного по множеству снимков, полученных с беспилотного летательного аппарата.









