Поиск точек на стереопаре снимков идеального случая съемки
Известно, что на стереопаре снимков идеального случая съемки (угловые элементы внешнего ориентирования снимков съемки равны нулю, а базис фотографирования параллелен оси Х системы координат объекта) ординаты ó соответственных точек равны и, как следствие, значения поперечных параллаксов для всех соответственных точек равны нулю. Очевидно, что при автоматической идентификации точек на стереопаре снимков область поиска на снимке ограничивается линией параллельной оси х снимка.
Преобразование (тр а н с ф о р м и р о в а н и е) исходной стереопары снимков в стереопару снимков идеального случая съемки очень широко применяется в цифровых фотограмметрических системах. Полученные таким образом стереопары снимков используются для выполнения работ по построению цифровых моделей рельефа и цифровых моделей объектов, так как при их использовании упрощается выполнение про- цессов идентификации соответственных точек на стереопаре снимков и создаются наиболее комфортные условия для стереонаблюдения и измерения снимков.
Для цифрового трансформирования снимков необходимо предва- рительно выполнить определение элементов взаимного ориентирования
снимков. врезультате цифрового трансформирования создается стереопа- ра снимков идеального случая съемки в системе координат фотограмме- трической модели, ось Х которой параллельна базису фотографирования.
использование базисных линий на нескольких перекрывающихся снимках
Если, предположим, имеется три перекрывающихся снимка, то
после измерений на втором сним- ке можно провести на третьем снимке две базисные линии по второму и третьему и первому и третьему снимкам (рис. 5.19). Здесь линия kl параллельна базису фотографирования B2, а линия np параллельна базису фотографирования B3. в резуль- тате соответствующая точка m3 получится как точка пересечения двух базисных линий.
Этот метод эффективен в цифровых интерактивных фотограмметрических системах (например, в системе CDW, Гер- мания) для обработки наземных снимков в режиме монокулярных измерений. Измерив координаты
S B1 S2
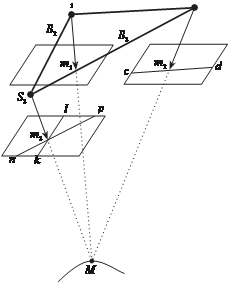рис. 5.19
точки m1 на левом снимке, на правом снимке проводится соответствую- щая базисная линия cd. Оператор находит соответствующую точку на правом снимке вдоль этой линии. На третьем снимке рисуются уже две базисные линии. Оператору (или коррелятору) остается только уточнить выбор соответственной точки в районе пересечения этих прямых.
сужение области поиска вдоль базисных линий
Рассмотрим возможность сужения области поиска вдоль базисной линии cd (см. рис. 5.19). Это можно сделать, если известны пределы из- менения объекта по глубине, т.е Zmin и Zmax (рис. 5.20).
Координаты концов участка базисной линии cd, вдоль которого
следует осуществлять поиск соответственной точки, вычисляются сле- дующим образом. Сначала, используя прямые формулы коллинеарности,
X = X
+ (Z - Z
) a11(x - x0 ) + a12 (y - y0 ) - a13f ;
S S a
(x - x ) + a
(y - y ) - a f
Y = Y
+ (Z - Z
31 0 32 0 33
) a21(x - x0 ) + a22 (y - y0 ) - a23f ,
(5.7.3)
S S a (x - x ) + a (y - y ) - a f
31 0 32 0 33
вычисляют координаты X, Y точек M c и M d, используя Zmin, Zmax соответ- ственно и координаты x, y точки m1 на левом снимке. Затем по обратным формулам
x = x
- f a11( X - X S ) + a21(Y - Y S ) + a31(Z - Z S ) ;
0 a ( X - X ) + a
(Y - Y ) + a (Z - Z )
13 S 23
S 33 S
(5.7.4)
y = y
- f a12 ( X - X S ) + a22 (Y - Y S ) + a32 (Z - Z S )
0 a ( X - X ) + a (Y - Y ) + a (Z - Z )
13 S 23 S 33 S
вычисляются координаты точек с и d на правом снимке.
Применяя автоматические методы отождествления одноименных точек вдоль отрезка базисной линии cd, находят соответственную точ-
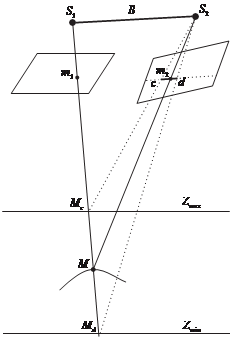ку m2. Естественно, чем точнее известны Zmin и Zmax, тем меньше отрезок cd и меньше время поис- ка соответственной точки. Если
точка изобразилась на трех и более снимках, то на третьем и последующих снимках соот- ветственная точка находится сначала как точка пересечения базисных линий, а затем ее по- ложение уточняется одним из ав- томатических методов отождест- вления одноименных точек.
Рассмотрим еще один при- мер решения задачи сужения области поиска соответствен- ных точек на паре снимков. Предположим, что требуется найти по паре снимков высоту Z точки местности, если у нее за-
рис. 5.20
даны плановые координаты X, Y.
в этом случае задаваясь Zmin и S1 S2
Zmax для данного участка мест- ности можно вычислить соот-
ветствующие точки на левом
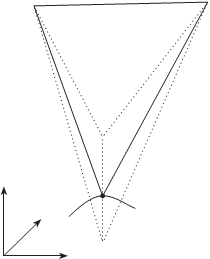
и правом снимках a, b и c, d (рис. 5.21), используя для это- го уравнения коллинеарности (5.7.4). Очевидно, что в пределах отрезков ab и cd существует только одна пара соответствен- ных точек, а именно — изображе-
ние точки М местности. Поэтому, Z
применяя один из методов ото- ждествления вдоль этих линий,
a b c d
Zmax
M
Y
находят соответственные точки m1, m2 и решают прямую засечку. Задачу можно решить гораздо быстрее, если задаться некото-
Zmin
|
O
рис. 5.21
рым шагом изменения высот точек местности ∆Z. Тогда для каждого значения Z i=Zmin+i∆Z (i=1÷n, n=(Zmax–Zmin)/∆Z) вычисляют значения коор- динат точек снимков по уравнениям (5.7.4) и коэффициенты корреляции для этих точек. Максимальное значение коэффициента корреляции укажет на соответствующие точки, а следовательно, и на точку М с искомой координатой Z (см. рис. 5.21). Шаг изменения координаты Z на первом этапе можно выбрать достаточно большим, затем уменьшить его до величины точности, с которой необходимо получить координату Z. Таким образом, получают координату Z с заданной точностью.
Рассмотренный алгоритм достаточно эффективен при создании цифровых моделей рельефа в виде регулярной сетки.
§5.8. Построение цифровой модели поверхности
На основе методов идентификации соответственных точек на со- седних снимках (см.§§5.4, 5.5) можно получить трехмерную модель объекта в виде плотной сети точек, покрывающую всю поверхность объекта, аналогично тому, как это получается в результате трехмерного лазерного сканирования. Для этого на объекте задается плотная сетка
с известными плановыми координатами X, Y и находятся соответству- ющие им координаты Z, используя методы, описанные выше. Однако, как известно, из-за различной перспективы снимков и рельефа объекта будут возникать проблемы при идентификации соответственных точек. Проблема может быть решена, если увеличить количество снимков объ- екта, полученных с различных точек фотографирования.
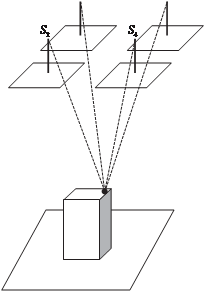
На рис. 5.22 видно, что изображения на парах перекрывающихся снимков S1–S2, S3–S4, S1–S4, S1–S3, S2–S3 вокруг интересующей нас точки различные, поэтому корреляция между ними будет низкая. Для пары снимков S2–S4 коэффициент корреляции будет максимальным, так как изображения вокруг интересующей нас точки идентичны. Этот вариант снимков используется для вычисления координаты Z данной точки.
Для повышения надежности идентификации соответственных точек рекомендуется выполнять съемку с продольным и попереч- ным перекрытиями не менее 60%. в этом случае существуют много комбинаций пар снимков при анализе корреляции для каждой точ- ки. Поэтому, например, в цифровой фотограмметрической системе
S1 S3
 |  |
б
 |
а в
рис. 5.22
INPHO (MATCH-T DSM) анализ корреляции для данной точки прово- дится по направлениям, указанным стрелками (см. рис. 5.22, в).
§5.9. методы автоматического отождествления соответственных точек, основанные
на выделении элементов изображения
Сущность этих методов состоит в следующем: сначала выделяются элементы изображений, а затем они отождествляются. в качестве эле- ментов изображения можно использовать точки, линии, полигоны и т.д. Для выделения этих элементов применяются различные операторы, с которыми осуществляется свертка изображений. Например, для вы- деления характерных точек существуют операторы Forstner, Moravic, Dreschler, Mar-Hildreth, SIFT и др. Задача этих операторов найти на изображении области с наибольшим изменением контраста, в которых затем получатся наилучшие результаты корреляции. выделенные с помощью о п е р а т о р а F o r s t n e r точки инвариантны к поворотам, и как следствие в этих точках корреляция получается более надежно. О п е р а т о р M o r a v е c позволяет выделить точки с контрастом, пре- вышающем некоторый порог. О п е р а т о р D r e s c h l e r вычисляет значение кривой Гаусса, которое позволяет определить точки, принад- лежащие перегибам линий. Эта характеристика линий не изменяется в зависимости от геометрических искажений, изменений масштаба и поворота изображения. О п е р а т о р M a r r - H i l d r e t h (или оператор LoG — лапласиан Гауссиана) фильтрует изображение и одновременно выделяет зоны изменений значений яркостей изображения. S I F T (мас- штабно-инвариантное преобразование) — это алгоритм, позволяющий описать точку снимка некоторыми локальными признаками, которые инвариантны к сдвигу, повороту и масштабу.
Существуют операторы (Roberts, Prewitt, Sobel, Canny и др.), кото- рые позволяют выделить линии и полигоны. Эти операторы основаны на выделении границ изменений значений яркостей изображения. За- дача этих операторов выделить участки на изображениях с наибольшим контрастом, в которых можно получить наилучшие результаты при автоматизированных методах измерений. в результате также сужается область поиска одноименных точек на паре снимков, что позволяет резко сократить время на вычислительный процесс.
После выделения элементов изображений применяются площадные алгоритмы отождествления соответственных точек. Ниже приводится краткое описание некоторых операторов.
оператор форстнера (Forstner)
Позволяет оценить степень корреляции данного пикселя с окру- жающими его пикселями в некоторой области, например, 5х5 пикселей (то есть позволяет выделить те пиксели изображения, где наилучшим образом с точки зрения точности и надежности будет выполнено ото- ждествление одноименных точек одним из площадных методов) и вы- числить ожидаемую точность этого отождествления.
Оператор Форстнера основан на анализе градиентного изображения для выбранной области вокруг данного пикселя. Для этого вычисляется матрица нормальных уравнений:
N æå g 2 å g xg ö
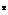
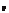
= ççå å 2 ÷÷, (5.9.1)
è g xg y g y ø
где g x, g y – составляющие градиента вдоль осей x и y, которые вычис- ляются по (5.6.7).
Обратная матрица к нормальным уравнениям, которая определяет точность измерений, вычисляется как
Q N 1 æ
å g 2
-å g xg ö
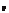
= -1 = çç x
2 ÷÷. (5.9.2)
N è -å g xg y
å g y ø
Оценку точности измерений можно выполнить, вычислив значе- ние w, которое характеризует величину (площадь) эллипса ошибок:
1 å g 2å g 2 - (å g g )2
 |
w =
l1 + l2
= SpN =
x y x y
å g 2 + å g 2
, (5.9.3)
x y
где |N| — определитель; SpN — след матрицы N.
Кроме этого можно вычислить параметр q, который характеризует сжатие эллипса ошибок:
|
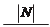
å g 2å g 2 - (å g g )2
| |
q = 4
= 4 x y
x y ;
0 £ q £ 1. (5.9.4)
|
(SpN )2
(å g 2 + å g 2 )2
Таким образом, оператор Форстнера позволяет на основе анализа величин w и q выполнить классификацию изображения и выделить зоны наилучшей корреляции. Например, чтобы избежать выполнения отождествления (корреляции) для пикселя, лежащего на границе где корреляция не определена вдоль этой границы, эллипс ошибок должен быть близок к кругу (q близка к 1) , а сама ошибка w — маленькой. Сле- дует отметить, что этот оператор инвариантен к поворотам изображения.
оператор моравика (Moravec)
Позволяет проанализировать изменение значений пикселей во- круг данного пикселя с координатами x, y. Как правило, анализируются пиксели по четырем направлениям — вдоль строк, столбцов и двух диагоналей вокруг данного пикселя. Изменения значений пикселей в каждом направлении вычисляется как сумма квадратов разностей между соседними пикселями:
n
M = 1 å2
m -1
|
å
éf ( x, y) - f ( x, y + 1)ù2 ;
 |
1 n (m -1) n m ë û
- 2 - 2
|
n -1 m
M = 1 å2
åéf ( x, y) - f ( x + 1, y)ù2 ;
 |
2 (n -1)m n m ë û
- 2 - 2
n -1 m -1
(5.9.5)
|
M = 1 å2 å
éf ( x, y) - f ( x + 1, y + 1)ù2 ;
 |
3 (n -1)(m -1) n m ë û
- 2 - 2
|
n -1 m -1
M = 1 å2 å
éf ( x, y + 1) - f ( x + 1, y)ù2 ;
| |
4 (n -1)(m -1) n m ë û
- 2 - 2
M = min (M1, M 2 , M 3 , M 4 ),
где n и m — число пикселей в фрагменте изображения вдоль оси x и вдоль оси y вокруг данного пикселя.
Далее выполняется сравнение значения M с некоторым пороговым значением и если М превышает это значение, то данный пиксель прини- мается как значащий (в котором следует проводить корреляцию) и ему присваивается значение «1», в противном случае — «0». Таким образом,
мы получаем матрицу зон изображения с наибольшим контрастом, в которых следует выполнять корреляцию.
оператор Дрешлера (Dreschler)
Позволяет вычислить значение кривой Гаусса для определения точки, принадлежащей перегибам поверхности и образованной значе- ниями пикселей в пределах исследуемого фрагмента изображения. Для этого определяется матрица (фрагмент изображения) размером n×m, для которой будет вычисляться значение кривой Гаусса, и этой матрицей проходят по всему изображению. Значение кривой Гаусса вычисляется по формуле
¶2f ¶2f - ¶2f
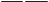
K = ¶x2 ¶y2 ¶x¶y
, (5.9.6)
|
æ æ ¶f ö2 æ ¶f ö2 ö
çç1 + çè ¶x ÷ø
ç ¶y ÷ ÷÷
где
è
¶f = 1 éëf ( x + 1, y) - f ( x -1, y)ùû ;
è ø ø
¶x 2
¶f = 1 éëf ( x, y + 1) - f ( x, y -1)ùû ;
¶y 2
 |
|
¶2f = éf ( + 1, y) + f ( -1, y) - 2f ( , y)ù;
¶x2 ë û
 |
|
¶2f = éf ( , y + 1) + f ( , y -1) - 2f ( , y)ù;
¶y2 ë û
¶2f = 1 éf ( + 1, y + 1) + f ( -1, y -1) - f ( -1, y + 1) - f ( + 1, y -1)ù.
 |
x x x x
¶x¶y 4 ë û
анализируя значения K, можно выделить пиксели, принадлежащие перегибам линий.
Из дифференциальной геометрии известно, что кривая Гаусса инвариантна к геометрическим искажениям.
оператор марра (LoG — Лапласиан гауссиана)
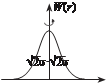Одновременно сглаживает (фильтрует) изображение и вы- деляет границы объектов. Он получается из второй произво- дной, симметричной сглажива- ющей функции Гаусса, откуда и происходит его название. На рис. 5.23 показаны кривая нор- мального распределения Гаусса и соответствующая ей кривая оператора LoG в двумерном про-
r r
рис. 5.23
странстве. Известно, что функция Гаусса (в трехмерном пространстве) образуется поверхностью вращения кривой нормального распределения и описывается выражением
W ( x, y) = W (r ) =
1
2ps2
- x2 +y2
e 2s2 ;
r 2 = x2 + y2 ,
(5.9.7)
где σ — ширина распространения функции Гаусса.
Дифференцируя (5.9.7) по x и y, получим:
W ¢( x, y) =- x
- x2 +y2
e 2s2 ;
W ¢ ( x, y) =- y
- x2 +y2
e 2s2 .
(5.9.8)
x 2ps4 y 2ps4
вторые производные имеют вид:
W ¢¢( x, y) =-
x2 - s2
- x2 +y2
e 2s2 ;
W ¢¢( x, ) =- y2 - s2
- x2 +y2
e 2s2
, (5.9.9)
|
x 2ps6 y 2ps6
по которым получается оператор лапласа (LoG):
LoG =
x2 + y2 - 2s2 2ps6
- x2 +y2
e 2s2
. (5.9.10)
Здесь единственная переменная — это σ, причем с помощью этой величины можно задавать масштаб фильтрации (сглаживания). выпол- няя свертку изображения с функцией (5.9.10), получим новое изобра- жение, в котором значения пикселей будут максимальны на границах, а перемена знака функции от пикселя к пикселю укажет на положение границы, которая лежит в месте пересечения графика функции с нуле-
вой плоскостью. Основная трудность при реализации данного подхода заключается в выборе значения переменной σ (масштабного коэффици- ента) функции (5.9.10). От нее зависит степень подробности выделения границ, а следовательно, и степень сглаживания изображения.
SIFT (масштабно-инвариантное преобразование)
Этот алгоритм позволяет описать точку снимка некоторыми ло- кальными признаками, которые инвариантны к сдвигу, повороту и масштабу.
1. выделение характерных точек на изображении, применяя один из описанных выше операторов, например, оператор Форстнера.
2. Описание локальной области, выделенной вокруг точки путем задания радиуса и ориентации локальной системы координат, связанной с этой локальной областью.
3. Детальное описание точки с помощью градиентов по направле- ниям, заданным относительно ориентации локальной области.
Рассмотрим подробнее каждый из этапов формирования SIFT- описания точки. выделение характерных точек на изображении вы- полняется путем применения одного из описанных выше операторов, например, оператора Форстнера. локальная область задается радиусом r окружности с центром в характерной точке и начальным направлением, заданным как направление максимального градиента.
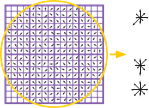
Описание точки задается в виде матрицы размером l×l элементов, которая формируется по исходной локальной области 4l×4l пикселей. На рис. 5.24 в качестве примера показано описание характерной точки размером 4×4 элемента, полученное по исходной локальной области 16×16 пикселей. Причем для каждого элемента описания вычисляются величины градиентов по восьми направлениям. Таким образом, для описания характерной точки в данном случае используется 4×4×8=128
|
признаков. вектор, описываю- щий точку, будет иметь размер- ность 128.
Описав таким образом все характерные точки на паре сним- ков, можно найти соответствен- ные точки, сравнивая вектора признаков. Следует также за-
рис. 5.24
метить, что данное описание точки не зависит от изменения яркости изображения, так как градиент является признаком инвариантным к изменению яркости.