29 30 31 32 33 34 35 / 66 35 36 37 38 39 40 41 42

Построение пирамиды изображений

Дата: 2025-06-02; Просмотры: 19

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

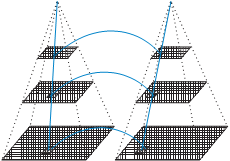Использование при автоматизации измерений соответственных точек на стереопаре снимков пирамиды изображений является одним из эффективных методов ускорения этого процесса. Пирамида изобра- жений представляет набор изображений, получаемых последовательно из исходных изображений путем преобразования и пропорционального уменьшения числа строк и столбцов. Например, следующее за исходным в пирамиде изображение получают объединением в один пиксель четы- рех пикселей исходного (значе-

ние пикселя принимают равным среднему арифметическому из четырех значений пикселей ис- ходного изображения). Таким же образом строятся последующие снимки пирамиды (рис. 5.16, a). На рис. 5.16, б показан пример пирамиды из четырех уровней для аэроснимка.

Измеренная на исходном левом изображении точка про- ектируется на снимок самого высшего уровня пирамиды и идентифицируется корреляци- онным методом с точностью до одного пикселя на втором снимке стереопары идентичного уровня

рис. 5.16

пирамиды. Учитывая, что изображение верхнего уровня имеет малые размеры (небольшое число строк и столбцов) поиск соответственной точки на этих снимках выполняется весьма быстро. Затем процесс иден- тификации продолжается на стереопаре нижнего уровня. Учитывая, что положение искомой точки известно с точностью до пикселя на снимке высшего уровня, область поиска локализуется на снимке пирамиды в пределах нескольких пикселей, что позволяет произвести быструю идентификацию соответственной точки на снимке. Таким же образом производят поиск на всех снимках пирамид изображений, закончив этот процесс на исходных снимках стереопары.

Этот метод часто используется при построении цифровых моделей рельефа по стереопаре снимков. На первом этапе отождествляют соот- ветственные точки на самом верхнем уровне пирамиды. Поскольку на верхнем уровне пирамиды число пикселей существенно меньше по срав- нению с исходными снимками, то отождествление можно выполнить для всех пикселей стереопары достаточно быстро. Затем для каждой пары соответственных пикселей данного уровня пирамиды находят 4 пикселя для каждого снимка на более нижнем уровне (в соответствии с методом формирования пирамиды). Среди этих пикселей находят пару соответственных пикселей методом корреляции и спускаются на следующий уровень. Таким образом доходят до исходных снимков. в результате имеем густую сеть соответственных точек пары снимков, для которых решается прямая засечка и получается ЦМР.

использование базисных линий на снимках стереопары

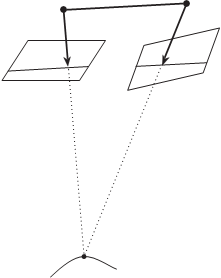
Известно, что если пара снимков и базис фотографирования вза- имно ориентированы, то любая пара соответственных точек находится в базисной плоскости, проходящей через базис фотографирования B и соответственные точки m1 и m2 на стереопаре снимков (рис. 5.17). Следы сечения снимков стереопары базисными плоскостями называют б а з и с н ы м и (или эпиполярными) линиями (линии a–b и c–d).

Очевидно, что, измерив точку на одном из снимков стереопары, можно провести через эту точку и центры проекции базисную плоскость и построить на другом снимке стереопары базисную линию, на которой будет находиться точка, соответственная измеренной на первом снимке. Для нахождения соответственной точки достаточно провести ее поиск вдоль найденной базисной линии.

Этот поиск выполняется следующим образом. По изме- ренным на первом снимке стере- опары координатам x1, y1 точки, вокруг которой формируется a эталонная матрица, известным значениям элементов внутренне-

го и взаимного ориентирования снимков и заданному значению координаты х c на втором снимке стереопары вычисляется значе- ние координаты ó c точки сним- ка, расположенной на базисной линии (рис. 5.18). Затем произ- водится формирование матрицы вокруг этой точки и вычисляется коэффициент корреляции R. За-

m1 d b

B S2

c m2 d

давая значение координаты х c с шагом один пиксель, осущест-

рис. 5.17

вляют поиск соответственной точки на снимке по базисной линии и находят на ней соответственную точку по максимуму коэффициента корреляции R.

Учитывая, что вследствие ошибок определения значений элементов взаимного ориентирования координата ó c может быть вычислена с ошиб- кой, для повышения точности определения координат соответственной точки производят формирование матриц в точках снимка со смещением центральной точки в пределах 1–2 пикселей по оси ó.

Формулу для вычисления координаты ó c получают следующим образом. Из рис. 5.18 следует, что векторы B, r1, r c компланарны, так как находятся в одной плоскости. Смешанное произведение этих век-

торов B(r1×r c)=0. в случае ис- пользования в качестве элемен- тов взаимного ориентирования

B S2