§5.6. вычисление градиента изображения
Градиент изображения широко применяется при реализации раз- личных способов автоматического измерения координат точек снимков, а также при выделении границ объектов по изображению. Рассмотрим методы вычисления градиента изображения.
Градиент изображения f(x, y) в точке (x, y) определяется как дву- мерный вектор
é g x ù
é¶f ù
ê ¶x ú
G [f(x, y)] = ê g ú = ê¶f ú.
(5.6.1)
ë y û ê ú
êë ¶y úû
Из векторного анализа известно, что вектор G указывает направле- ние максимального изменения функции f в точке (x, y); g x, g y — состав- ляющие градиента по осям x и y; ∂f/∂x и ∂f/∂y — первые производные
от изображения f по координатам x и y.
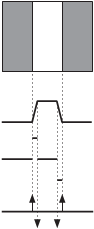
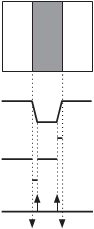
Рис. 5.12 поясняет смысл производных изображения, здесь приве- дены изображения светлого объекта простой формы на темном фоне, кривая яркостей изображения вдоль горизонтальной линии, а также пер- вая и вторая производные этой кривой. Следует отметить, что участки кривой, соответствующие границе (переход от темной области к светлой и наоборот), представляют собой наклонные, а не вертикальные линии, какие должны быть в случае резкого изменения яркости изображения. Это связано с тем, что границы на цифровом изображении в результате
дискретизации обычно слегка размыты.
Первая производная всех участков кривой с постоянной яркостью равна нулю и является постоянной величиной на участ- ках изменения яркости. С другой стороны, вторая производная равна нулю на всех участках, кроме начальных и конечных то- чек изменения яркости. С учетом этого, очевидно, что величина первой производной может быть использована для обнаружения наличия границ объектов на
Объект
Кривая яркости вдоль горизонтальной линии
Первая
производная
вторая производная
рис. 5. 12
изображении, а знак второй производной – для определения, на темной (фон) или на светлой (объект) стороне границы располагается пиксель границы. Например, знак второй производной (см. рис. 5.12) положителен для пикселей, расположенных на внешних сторонах границ объекта, и отрицателен для пикселей внутренних светлых сторон этих границ. Те же рассуждения справедливы для случая нахождения темного объекта на светлом фоне. Отметим, что знак второй производной при этом также позволяет определить переход яркости на границе.
На практике при определении границ часто вычисляют величину вектора G, называемого обычно градиентом:
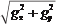G = (5.6.2)
или для упрощения вычислений градиент аппроксимируется абсолют- ными значениями
G @ g x + g y . (5.6.3)
вычисление составляющих градиента (первых производных) можно выполнить несколькими способами. Один из подходов состоит в использовании разностей яркостей между соседними пикселями:
g = ¶f = f(x, y) - f(x -1, y);
x ¶x
g = ¶f = f(x, y) - f(x, y -1).
y ¶y
(5.6.4)
Однако на практике чаще используют другой подход, основанный на свертке исходного изображения размером 3×3 пикселя с маской (оператором) с центром в точке, имеющей координаты x, y. Такой под- ход менее чувствителен к фотометрическим шумам, которые присущи любым изображениям. Здесь градиент вычисляется не из двух соседних пикселей, а из анализа всех 9 пикселей, окружающих точку с коорди- натами x, y:
G = éf(x, y) * H x ù = é g x ù , (5.6.5)
|
|
|
êf(x, y) * H ú
ê ú
ë y û
где * — знак свертки; H x, H y — маски (операторы, фильтры).
в качестве примера маски приведем оператор Собеля, как наиболее
часто употребимый при вычислении градиентов:
é-1 0 1ù
H x = ê-2 0 2ú;
é 1 2 1 ù
H y = ê 0 0 0 ú.
(5.6.6)
ê ú ê ú
êë-1 0 1úû
êë-1 -2
-1úû
Свертка вычисляется по следующей формуле:
n m
g x = f(x, y)* H x = ååf(x, y)ij H xij ;
i =1 j =1
n m (5.6.7)
g y = f(x, y)* H y = ååf(x, y)ij H y ij ,
i =1 j =1
где n — число строк; m — число столбцов в маске (для оператора Со- беля n=m=3).
Если взять фрагмент изображения f размером 3×3 с координатами центрального пикселя x, y, то составляющие градиента для этого пик- селя, с учетом (5.6.6) и (5.6.7), можно вычислить следующим образом:
éf1
|
f(x, y) = êf4
êëf7
f2 f3 ù
|
f5 f6 ú;
f8 f9 úû
(5.6.8)
g x = f(x, y)* H x = (f3 + 2f6 + f9 ) - (f1 + 2f4 + f7 );
g y = f(x, y)* H y = (f1 + 2f2 + f3 ) - (f7 + 2f8 + f9 ).
(5.6.9)
Приведем некоторые другие примеры операторов: оператор Прайвита
é-1 0 1ù
H x = ê-1 0 1ú;
é 1 1 1 ù
H y = ê 0 0 0 ú;
(5.6.10)
ê ú ê ú
êë-1 0 1úû
оператор Робертца
êë-1 -1
-1úû
H = é 0 1ù;
H = é1 1 ù. (5.6.11)
x ê-1 0ú
x ê0 -1ú
ë û ë û
На рис. 5.13, а показан фрагмент цифрового снимка с изображе- нием квадрата. Здесь пиксели, у которых значение яркости равно 10, принадлежат фону, а с яркостью равной 20 — объекту (квадрату). На рис. 5.13, б показано соответствующее градиентное изображение, по- лученное путем свертки исходного изображения с оператором Робертца (5.6.11), а величина самого градиента вычислялась по (5.6.3).
 |  |
а б
рис. 5.13
На рис. 5.14 показан пример работы оператора Собеля (рис. 5.14, а — исходный снимок; рис. 5.14, б — градиентное изобра- жение, полученное в результате обработки исходного изображения оператором Собеля; рис. 5.14, в — составляющая градиента вдоль оси x; рис. 5.14, г — составляющая градиента вдоль оси y).
 |  |
а б
в г
рис. 5.14
§5.7. методы, позволяющие сузить область поиска соответственных точек на смежных снимках
использование априорной информации о параметрах съемки
Для сужения области поиска соответственных точек на правом снимке и, как следствие, снижения времени поиска соответствен- ных точек на стереопаре снимков, можно использовать имеющуюся предварительную информацию о параметрах съемки. Например, если известна величина продольного перекрытия между снимками (рис. 5.15, а), то соответствующие точки на правом снимке следует ис- кать не по всей площади снимка, а только в пределах этого перекрытия вдоль оси x. Зная возможные пределы изменения поперечных параллак- сов ∆q, можно ограничить область поиска вдоль оси y (заштрихованная область на рис. 5.15, б). Если известны превышения точек изображенной на снимках стереопары местности, можно вычислить максимальное зна- чение разностей продольных параллаксов ∆p соответственных точек и
|
ограничить область поиска вдоль оси x (заштрихованная область на рис. 5.15, в).
На практике для ограни-
а
чения области поиска соответ-
ственных точек на паре снимков
| Δ Δp | q |
б в
рис. 5.15
чаще всего используют пирамиду изображений и базисные линии (если известны элементы взаимного ориентирования снимков).
Рассмотрим более подробно эти подходы к выбору области поиска соответственных точек на паре снимков.