§5.5. отождествление соответственных точек по методу наименьших квадратов в пространстве объекта
Как отмечалось выше, геометрические искажения (несоответствия) двух фрагментов снимков можно учесть при отождествлении одноимен- ных точек по методу наименьших квадратов, используя перспективные преобразования. Для этого расширяют модель данного метода за счет включения в исходное уравнение уравнений коллинеарности. Такой подход позволяет выполнить отождествление сразу для множества
 одноименных точек, учитывая не только фотометрическое соот- ветствие точек, но и геометрию построения фотограмметриче- ской модели.
одноименных точек, учитывая не только фотометрическое соот- ветствие точек, но и геометрию построения фотограмметриче- ской модели.
Такая модификация метода наименьших квадратов чаще всего применяется при постро- ении цифровой модели рельефа и ортофотоплана (ортофото). Соотношение между яркостями
 Z
Z
X
рис. 5. 11
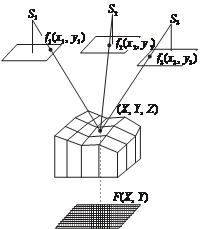
изображения F(X, Y) на ортофото точек местности (X, Y, Z) и ярко- стями соответствующих точек на исходных снимках f i(x i, y i) может быть записано следующим об- разом (рис. 5.11):
F ( X ,Y ) - k i f i (x i , y i ) = 0,
(5.5.1)
где k i — коэффициенты фотометрических преобразований; i — номер снимка;
x = x
- f a11( X - X Si ) + a21(Y - Y Si ) + a31(Z - Z Si ) ;

|
|
|
i 0 ( X - X
) + a23
(Y - Y Si
) + a33
(Z - Z Si )
(5.5.2)
y = y
- f a12 ( X - X Si ) + a22 (Y - Y Si ) + a32 (Z - Z Si ) .

|
|
|
i 0 ( X - X
) + a23
(Y - Y Si
) + a33
(Z - Z Si )
Предположим, что элементы внутреннего и внешнего ориенти- рования снимков известны, тогда в уравнениях (5.5.1) с учетом (5.5.2)
неизвестными являются: яркость пикселя на ортофото F с заданными координатами X, Y; отметка Z соответствующей точки местности и коэффициенты k i фотометрических преобразований снимков, причем для одного из снимков этот коэффициент фиксируют, приняв равным единице, чтобы избежать неопределенности в определении этих коэф- фициентов.
Уравнение (5.5.1) можно составить для каждого пикселя ортофото. Для этого сначала по координатам X, Y пикселя ортофото определяют приближенную высоту Z0 соответствующей точки местности, ис- пользуя для этого приближенную цифровую модель рельефа. Затем по уравнениям (5.5.2) вычисляют координаты соответствующих точек на исходных снимках, по которым берется (методом двойного линейного интерполирования) яркость f i.
Уравнение (5.5.1) нелинейно относительно неизвестных, поэтому
переходят к линейным уравнениям поправок
a1dF + a2dZ + a3dk i + l = v, (5.5.3)
которые решают по методу наименьших квадратов способом последова- тельных приближений. в результате находят яркости пикселей ортофото и соответствующие высоты точек местности.
Если элементы внешнего ориентирования снимков неизвестны, то их можно найти совместно с решением основной задачи по построению ортофото и ЦМР на основе уравнений (5.5.1). Тогда уравнения поправок примут вид:
a1dF + a2dZ + a3dk i + a4dX S + a5dY S + a6dZ S + a7da + a8dw + a9dk + l = v. (5.5.4)
Кроме того, в этом случае к общей системе уравнений (5.5.4) следует добавить обычные уравнения поправок для опорных точек, полученные из уравнений коллинеарности (5.5.2). Данный метод отождествления одноименных точек с одновременным построением цифровой модели ре- льефа реализуется в случае, если на данный участок местности имеется более двух снимков. Для двух снимков общее число неизвестных, под- лежащих одновременному определению, превышает число уравнений. Число неизвестных N можно подсчитать по формуле N=2P+(S– 1)+6S,
где P — число точек ЦМР, подлежащих определению (число пикселей ортофото); S — число снимков. Число уравнений M=PS.
Предположим, например, что мы хотим построить ЦМР, состоя- щую из 100 точек (Р=100) по двум снимкам (S=2), при этом элементы внешнего ориентирования снимков известны, тогда N=2×100+(2–1)=201; M=100×2=200.
Таким образом, задача по двум снимкам не решается (N>M). Если добавить третий снимок, то максимальное значение М (если все точки изобразились и на третьем снимке) будет равно 300. в этом случае за- дача решается (N<M).
Слабым местом метода является необходимость знания хороших начальных приближений для цифровой модели рельефа и большое число приближений. Для уменьшения числа приближений в этом методе часто применяют пирамиду исходных изображений.








