АвтомАтизАция фотогрАмметрических измерений
автоматизация измерений координат точек снимков позволяет в значительной мере уменьшить степень участия оператора и, как след- ствие, значительно повысить производительность выполнения работ. Фотограмметрические процессы выполняются, как известно, на основе монокулярных и стереоскопических измерений.
М о н о к у л я р н ы е и з м е р е н и я координат точек снимков применяются при выполнении процесса внутреннего ориентирования снимков (измерение координат координатных меток), измерении коор- динат маркированных точек, особенно при решении прикладных задач по наземным снимкам, при калибровке съемочных камер (измерение координат маркированных точек тест-объекта) и т.п. автоматизация монокулярных измерений практически сводится к автоматическому нахождению на снимке изображения маркированной точки (в виде геометрической фигуры: круг, крест, треугольник и т.д.) и вычислению геометрического центра этих точек.
С т е р е о с к о п и ч е с к и е и з м е р е н и я применяются при вы- полнении практически всех фотограмметрических процессов (взаимное ориентирование пары снимков, внешнее ориентирование модели, по- строение цифровых моделей рельефа, рисовка контуров и др.). Задача автоматизации стереоскопических измерений — автоматическое оты- скание на паре снимков идентичных (соответственных) точек.
§5.1. корреляционный метод измерений соответственных точек на паре снимков
в настоящее время в цифровых фотограмметрических системах в подавляющем большинстве случаев используются методы авто- матической идентификации соответственных точек, основанные на сравнении значений одноименных пикселей идентичных по размеру фрагментов цифровых снимков вокруг измеряемых точек (эти ме- тоды иногда называют площадными методами). Такими методами являются корреляционный и метод наименьших квадратов. Они широко применяются в цифровых фотограмметрических системах. Рассмотрим сначала к о р р е л я ц и о н н ы й м е т о д измере-
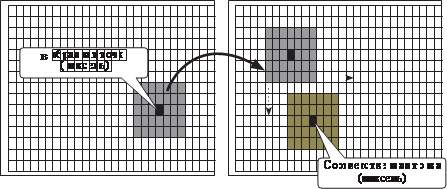
ний соответственных точек на паре снимков. На рис. 5.1 показан принцип отождествления соответственных точек на паре снимков, который заключается в следующем. На одном из снимков стереопа- ры измеряется любая точка (см. рис. 5.1, а), затем вокруг этой точки (см. рис. 5.1, б) формируется фрагмент изображения в виде ма- трицы, которую будем называть эталонной, и накладывается на второй снимок (см. рис. 5.1, в). Эталонную матрицу перемещают по второму снимку (в пределах области поиска) с шагом один пиксель (рис. 5.2) и каждый раз сравнивают соответствующие яркости перво- го и второго снимков в пределах размеров эталонной матрицы. Если все яркости совпадают, то это означает, что найдена соответственная (идентичная) точка на втором снимке (см. рис. 5.1, г). Критерием ре- шения задачи может служить разность соответствующих яркостей пикселей двух фрагментов изображений, которая должна быть равна нулю для идентичных точек. Однако на практике в качестве критерия применяется значение коэффициента корреляции R, которое менее подвержено влиянию шумов изображений.
Положение матрицы, при котором значение коэффициента корреляции максимально, соответствует матрице, построенной вокруг соответственной точки на втором снимке стереопары. Таким образом находят координаты соответственной точки на правом снимке. Коэффициент корреляции R изменяется в пределах от 0 до 1 и вычисляется по формуле
 |  | ||
а б
в г
рис. 5.1
 |
Снимок 1 Снимок 2
рис. 5.2
å D1 ( x1, y1 )i D2 ( x2 , y2 )i
R = 1 ,
(5.1.1)
n n
å D2 ( x1, y1 ) å D2 ( x2 , y2 )
1 i 2 i
1 1
где D1, D2 — яркости пикселей соответственно первого и второго цифровых снимков стереопары; i — номер пикселя в матрице; n — ко- личество пикселей в матрице (например, матрицы размерностью 5´7, изображенной на рис. 5.2, n=35); x1, y1 и x2, y2 — пиксельные координаты элементов матрицы на первом и втором снимках.
Для компенсации различия в значениях коэффициентов контраст- ности снимков стереопары, коэффициент корреляции вычисляют по нормализованным значениям яркостей каждого пикселя. Нормализо- ванные значения яркостей каждого пикселя получают путем вычитания из значений яркостей каждого пикселя среднего значения яркостей всех пикселей матрицы:
å[D1 ( x1, y1 )i - D1¢][D2 ( x2 , y2 )i - D2¢ ]
R = 1 ,
n n
(5.1.2)
å[D1 ( x1, y1 ) - D1¢]2å[D2 ( x2 , y2 ) - D2¢ ]2
где D¢ = 1 ån
1
D ( x , y ) ;
i
D¢ = 1 ån
i
1
D ( x , y ) .
n 1 1 1 1 i n 1 2 2 2 i
С геометрической точки зрения формулы (5.1.1) и (5.1.2), по которым вычисляется коэффициент корреляции, являются скалярным произ- ведением двух n-мерных векторов, координатами которых, в нашем случае, являются значения элементов двух сравниваемых матриц, то есть значения яркостей каждого из элементов матриц. Из аналитической геометрии известно, что скалярное произведение двух векторов является косинусом угла между ними. При равенстве координат векторов два вектора совпадают и поэтому значение угла между ними равно нулю, а значение косинуса равно единице.
По методике поиска соответственных точек на стереопаре снимков, изложенной выше, можно получать координаты соответственных точек с точностью до одного пикселя. Для получения координат с подпиксель- ной точностью можно уменьшить шаг перемещения матрицы, например,
установить его равным 0,5 пик- селя. в этом случае необходимо увеличить исходное цифровое изображения в два раза, т.е. один пиксель исходного изображения занимает 2´2 пикселей в увели- ченном изображении.
На рис. 5.3 показан пример получения увеличенного в два раза изображения. Если осущест- влять поиск соответственных точек на стереопаре снимков по таким изображениям, то точ-
|
|
| |||||
|
|
|
| ||||
|
|
|
| ||||
|
|
| |||||
|
|
| |||||
рис. 5. 3
ность определения координат будет равна 0,5 пикселя.
Более широко в цифровых фотограмметрических системах при- меняют другой метод идентификации соответственных точек на сте- реопаре снимков с подпиксельной точностью. в этом методе, сначала находят пиксель, соответствующий максимальному значению коэффи- циента корреляции Rmax. Затем в пределах 2–3 пикселей относительно этого пикселя вдоль осей x и y берут соответствующие им значения коэффициента корреляции R i. Зависимость значений коэффициентов корреляции R i от значений координат х и ó описывают обычно полино- мами второй степени.
R = a0 + a1x + a2 x2 ;
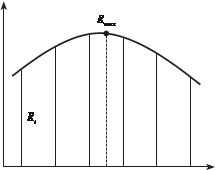На рис. 5.4 графически пред- ставлена зависимость (5.1.3) R коэффициента корреляции R от координаты х.
Для определения коэффи- циентов полиномов (5.1.3) по значениям координат х и ó и ко- эффициентам корреляции R i со- ставляют две системы уравнений (отдельно для осей х и ó):
|
a0 + a1x + a2 x2 - R = v x ;
R = b0 + b1y + b2y2.
(5.1.3)
b + b y + b y2 - R = v . (5.1.4)
0 1 2 y
рис. 5. 4
Значения коэффициентов полиномов находят в результате решения системы линейных уравнений (5.1.4) по методу наименьших квадратов. Значения координат соответственной точки на изображении с подпик- сельной точностью находят как максимумы (локальные экстремумы) функций (5.1.3). Для этого воспользуемся известным положением, что производные функций (5.1.3) в точке локального экстремума Rmax равны нулю, то есть :
xmax
=- a1 ;
2a2
ymax
=- b1 .
2b2
(5.1.5)
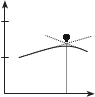
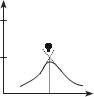
На рис. 5.5 показаны возможные случаи при вычислении макси- мального коэффициента корреляции. Первый вариант (см. рис 5.5, а) соответствует малоконтрастным изображениям. в этом случае макси- мальное значение коэффициента корреляции определяется ненадежно (с большой погрешностью) и как следствие ненадежно отождествление. второй вариант (рис. 5.5, б) гораздо лучше, чем первый (несмотря на меньшее абсолютное значение максимального коэффициента корреля- ции), так как у корреляционной функции ярко выраженный максимум. Поэтому при реализации алгоритма отождествления одноименных
точек на основе метода корре-
R
1
0,5
R
1
0,5
ляции при принятии решения о соответствии точек следует ана- лизировать не только величину максимального коэффициента корреляции, но и крутизну кор- реляционной функции. Крутизну
0 x 0
а б
рис. 5. 5
x функции можно оценить, напри- мер, по углу φ (см. рис. 5.5), чем меньше этот угол, тем лучше отождествление.
§5.2. измерение соответственных точек по методу наименьших квадратов
Идея метода заключается в нахождении продольного и поперечного параллаксов путем минимизации разности между яркостями фраг- ментов изображений двух снимков под известным условием VTV = min. Другими словами находится такое положение и форма матрицы поиска
(фрагмента изображения на втором снимке), при котором разности ярко- стей этого фрагмента и соответствующих яркостей эталонной матрицы (фрагмента изображения на первом снимке) будут минимальны.
Для этого решается система уравнений вида:
f1 ( x1, y1 ) - f2 ( x2 , y2 ) = 0,
(5.2.1)
где x2 = x1 - p, y2 = y1 - q; f1 ( x1, y1 ) — функция распределения яркос-
тей D1 в пределах фрагмента изображения с центром в измеряемой точке первого снимка с координатами x1, y1; f2 ( x2 , y2 ) — функция рас- пределения яркостей D2 в пределах фрагмента изображения с центром в соответствующей точке второго снимка с координатами x2, y2; p — продольный параллакс; q — поперечный параллакс.
Сначала предположим, что p и q не изменяются в пределах эталон- ной матрицы (фрагмента изображения вокруг измеряемой точки), т.е. предположим, что имеем идеальную пару снимков равнинной местности (отсутствуют углы наклона и разность высот фотографирования). Тогда параллаксы можно найти из решения уравнений (5.2.1). Закон изменения яркостей изображений (функции f) в зависимости от координат точек снимков нам естественно неизвестен, и он носит нелинейный характер. Однако нам известны дискретные значения этих функций (яркости) для пикселей с координатами x i, y i. Это позволяет составить уравнения (5.2.1) для каждого пикселя фрагментов изображений. Поскольку уравнения (5.2.1) являются нелинейными относительно неизвестных, то переходят к линейным уравнениям поправок, которые можно записать в виде a1dp + a2dq + = v или в общем виде
A2d+ L = V , (5.2.2)
где A2 — матрица частных производных от правого снимка по парал- лаксам; δ — поправки к неизвестным; L — свободные члены (значения функции (5.2.1) вычисленные по приближенным значениям неизвест- ных); V — невязки уравнений;
é¶f i ¶f i ù
2 2
ê ¶p ¶q ú
é g i
g i ù
éf i - f i ù
ê ú ê x y ú
éd ù 1 2
|
A = ê................ú = ê...........ú ;
d = ê
p ú;
ê ú
...........
2 ê ú ê ú
êëdq úû ê ú
ê¶f n
¶f n ú
g n g n
êf n - f n ú
2 2 ë x y û
ê ú
ë 1 2 û
ë ¶p ¶q û
i= 1÷n; n — количество пикселей в эталонной матрице; g x, g y — состав- ляющие градиента второго изображения в пикселе i.
Решение находится как
|
|
d= (AT A )-1 AT L. (5.2.3)
Далее на величины этих поправок уточняют неизвестные параллак- сы и переходят к следующему приближению. Для реализации второй и последующих итераций формируют матрицу поиска на правом снимке с уточненными координатами пикселей:
x2 = x1 - p + d p ;
y2 = y1 - q + dq .
Для получения яркостей изображения матрицы поиска обычно используют двойное линейное интерполирование. На рис. 5.6 показано положение ма- трицы поиска на правом снимке
на нулевой итерации — f0 (x y )
|
2 2 2
рис. 5.6
и после i-й итерации — f i (x y ). Так поступают до тех пор, пока поправки не станут прене- брегаемо малыми величинами.
в результате находят уравненные значения параллаксов.