§4.5. цифровое ортофототрансформирование снимков с использованием цифровой модели поверхности
в последнее время широко распространились методы создания цифровой модели поверхности (ЦМП) по снимкам местности в виде плотного облака точек. Каждая точка этого облака имеет три коорди-
наты X, Y, Z в системе координат объекта и яркость изображения в данной точке d. Методы создания таких облаков точек будут рас- смотрены в главе 5. Плотность такой ЦМП может достигать размера пикселя исходного изо-
ЦМП
Ортофото
M
M
d d
M0 M0
рис. 4.14
бражения на местности. Тогда построение ортофото может быть выпол- нено путем простого ортогонального проектирования облака точек на регулярную сетку ортофото (рис. 4.14). Для этого достаточно перенести яркости d с облака точек на ортофото по координатам X,Y. Очевидно, что координаты точек ЦМП не будут совпадать с соответствующими координатами пикселей ортофото, т.е. они не будут кратными размеру пикселя ортофото Δ, так как получаются путем решения прямых фото- грамметрических засечек. Поэтому в случае п р я м о г о т р а н с ф о р - м и р о в а н и я яркость переносится методом накопления (см. §4.2), т.е. когда яркость каждой точки ЦМП (облака точек) М переносится в ортофото пропорционально разностям координат X,Y этой точки и координат четырех соседних пикселей ортофото.
Ортофото можно сформировать и на основе применения принципа о бр а т н о г о т р а н с ф ор м и р о в а н и я. в этом случае для каждого пикселя ортофото М0 с координатами X0, Y0 выбираются точки ЦМП, лежащие в радиусе размера пикселя ортофото Δ. По этим точкам вы- числяется среднее значение яркости, которое присваивается пикселю ортофото. Для повышения точности формирования ортофото можно вместо среднего значения яркости использовать средневзвешенное значение в зависимости от расстояния между центром пикселя орто- фото с координатами X0, Y0 и данной точкой ЦМП с координатами X, Y или выполнить аппроксимацию яркостей. С другой стороны, если для формирования яркости данного пикселя ортофото попало несколько точек ЦМП с разными Z, то это
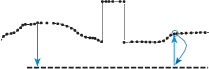говорит о том, что точки принад-
лежат вертикальной плоскости (см. рис. 4.14), например, стене дома. в этом случае яркость
M
ЦМП M
d d
следует взять у точки ЦМП с максимальной Z, которая будет
Ортофото
|
0
M0
рис. 4.15
DTMOrtho DSMOrtho
рис. 4.16
принадлежать крыше дома. Другим вариантом решения проблемы мо- жет быть предварительное автоматическое редактирование ЦМП путем выделения и удаления точек, принадлежащих отвесным плоскостям (рис. 4.15).
На рис. 4.16 показан пример построения ортофото в программ- ном продукте UltraMap с использованием цифровой модели рельефа (DTMOrtho) и цифровой модели поверхности (DSMOrtho). Безусловно построение ортофото на основе ЦМП дает наилучший результат в смыс- ле положения искусственных сооружений на ортофотоплане, однако, это требует пока значительных затрат по редактированию плотной цифровой модели поверхности в виде облака точек.
§4.6. создание цифровых фотопланов
Цифровым фотопланом называется цифровое трансформирован- ное изображение местности (объекта), созданное по перекрывающимся исходным снимкам. Цифровые фотопланы могут быть сформированы из трансформированных изображений, созданных по каждому из пере- крывающихся снимков, или путём формирования фотоплана непо- средственно в результате трансформирования всех перекрывающихся исходных снимков. На рис. 4.17 представлен принцип формирования цифрового фотоплана по трансформированным изображениям, создан- ным по каждому из перекрывающихся снимков.
Для создания фотоплана используются цифровые трансформи- рованные изображения снимков с одинаковым размером пикселей и имеющие координаты начал систем координат цифровых изображений O1 и O2 кратные размеру пикселя. При создании цифрового фотоплана в зоне перекрытия трансформированных изображений снимков проводят
линию пореза в виде полилинии с узлами K i (см. рис. 4.17). Затем, в каждой строке определяют гра-
Y
OM O2
ничные пиксели, совмещенные O1
с линией пореза, и приступают к формированию матрицы циф- рового фотоплана.
Координата начала системы координат цифрового фотоплана
|
|
K2
 |
P1 K3
X OM
принимается равной наи- K4
|
|
меньшему значению координат X
X O1
и X O2
начал систем координат
— трансформированный снимок 1; — трансфор- мированный снимок 2; — граничные пикселы
цифровых трансформированных
изображений снимков, а Y OM — наибольшему значению координат Y O1 и Y O2 .
рис. 4.17
Формирование цифрового фотоплана производят следующим об-
разом. Каждая строка матрицы фотоплана формируется из строки транс- формированного изображения снимка P1, включая граничный пиксель и строки изображения снимка P2, начиная с пикселя, следующего за граничным. Описанным методом можно присоединить к созданному фотоплану другие перекрывающиеся изображения снимков.
Цифровые фотопланы могут быть созданы путем формирования матрицы цифрового фотоплана непосредственно по всем перекрыва- ющимся исходным цифровым
|
снимкам. Рис. 4.18 иллюстрирует процесс формирования цифрово- го фотоплана этим методом.
в рассматриваемом методе
на перекрывающихся цифровых изображениях снимков проводят X линии пореза, которые пред- ставляют собой полилинии. По координатам узлов полилинии
в системе координат цифрового снимка определяют координаты проекций узлов полилинии на O цифровом фотоплане в системе
Исходные цифровые снимки
P1 P2 P3
Y
Цифровой фотоплан
рис. 4.18
координат объекта и формируют полилинии на цифровом фотоплане. По этим полилиниям определяют граничные пиксели, которые фор- мируют границы участков цифрового фотоплана, создание которых будет производиться по соответствующим цифровым изображениям снимков. Формирование цифрового фотоплана в пределах каждого из этих участков производится аналогично процессу формирования циф- рового ортофотоснимка (см. §4.3).
Определение координат X, Y узлов полилинии в системе координат цифрового фотоплана по значениям координат x, y их изображений в системе координат снимка производится методом приближений следу- ющим образом. Сначала вычисляются значения координат X, Y узла в системе координат цифрового фотоплана по формулам
X = X
+ (Z - Z
) X ¢ ;
Y = Y
+ (Z - Z
) Y ¢ , (4.6.1)
S S Z ¢
é X ¢ù é x - x0 ù
S S Z ¢
в которых ê Y ¢ ú = A êy - y0 ú.
ê ú ê ú
êë Z ¢ úû ê -f úû
в первом приближении значение высоты узла принимают равной среднему значению высот точек цифровой модели рельефа Z1 (рис. 4.19). По вычисленным значениям X1, Y1 по цифровой модели рельефа мето-
дом билинейной интерполяции
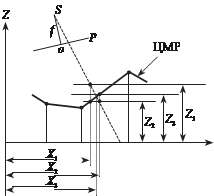(см. §4.3), определяют уточнен- ное значение высоты узла Z2, по которому по формулам (4.6.1) определяют уточненное значе- ние координат узла X2, Y2. По координатам X2, Y2 узла, в свою очередь, определяют новое зна- чение высоты узла Z3. вычисле-
O X
рис. 4.19
ние продолжают до тех пор, пока
разность значений координат X и Y узла в приближениях не будут превышать установленно- го допуска.