§4.3. цифровое ортофототрансформирование снимка
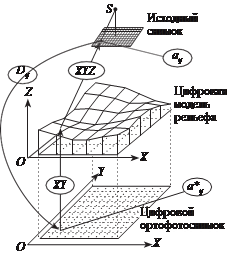
в результате цифрового ортофототрансформирования исходный снимок преобразуется в цифровое изображение местности, представ- ляющее собой ортогональную проекцию местности на горизонтальную плоскость. Принципиальная схема цифрового ортофототрансформиро- ванния снимков представлена на рис. 4.5.
Исходными материалами при цифровом трансформировании снимков служат:
цифровое изображение исходного фотоснимка;
 цифровая модель рельефа (ЦМР);
цифровая модель рельефа (ЦМР);
значение элементов вну- треннего и внешнего ориентиро- вания снимков;
значение параметров вну- треннего ориентирования сним- ка в системе координат цифрово- го изображения.
в большинстве случаев при трансформировании снимков используется цифровая модель местности в виде матрицы вы- сот, представляющая собой регулярную сетку квадратов на местности, стороны которых па-
рис. 4.5
раллельны осям X и Y системы координат объекта ОXYZ (см. рис. 4.5), в каждом узле которой определена высота. Координаты и высоты узлов сетки квадратов определены в системе координат объекта.
Для формирования ЦМР в виде матрицы высот в большинстве случаев используют цифровые модели рельефа, созданные в результате стереофотограмметрической обработки снимков по уже существую- щим топографическим картам или по данным воздушного лазерного сканирования.
Наиболее распространённым в настоящее время методом пред- ставлеения цифровых моделей рельефа местности является метод триангуляции Делоне, в котором рельеф местности представлен в виде пространственной сети треугольников, координаты и высоты вершин которых определены в системе координат объекта. Рельеф местности в пределах треугольника в этом виде ЦМР аппроксимируется пло- скостью, проведённой через его вершины. На рис. 4.6 показан пример представления цифровой модели рельефа в виде триангуляции Делоне. При формировании ЦМР этим методом по высотным пикетам треуголь- ники генерируются так, чтобы
|
в окружность, проведенную через вершины треугольника, не попадали вершины других треугольников.
По цифровой модели релье- фа в виде триангуляции Делоне можно сформировать ЦМР в виде матрицы высот.
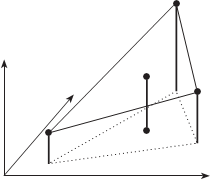
Для определения высоты узла i матрицы высот, по коорди- натам X i и Y i этого узла в системе координат объекта находят вер- шины треугольника триангуля- ции Делоне, в котором находится узел i (рис. 4.7). Значение высоты узла i определяют по формуле
Z i = A + BX i + CY i. (4.3.1)
рис. 4.6
Z
Z i
Y
Z1 i
O
рис. 4.7
Z3 выражение (4.3.1) представ- ляет собой уравнение плоскости, проведенной через вершины треугольника внутри которого находится узел i. Коэффици-
 Z2 енты уравнения (4.3.1) A, B и C получают в результате решения системы из трёх уравнений
Z2 енты уравнения (4.3.1) A, B и C получают в результате решения системы из трёх уравнений
A + BX + CY ─ Z = 0,
составленных по значениям ко-
X ординат X, Y и высот Z каждой из вершин треугольника.
Цифровое трансформирова- ние снимка выполняется следую-
щим образом. Сначала формируется прямоугольная матрица цифрового трансформированного изображения, строки и столбцы которой парал- лельны осям X и Y системы координат объекта, а координаты одного из углов матрицы заданы в этой же системе координат. Размер элементов (пикселей) матрицы обычно выбирают приблизительно равным вели- чине D×m, где D — размер пикселя цифрового изображения исходного снимка; m — знаменатель среднего масштаба снимка. Значения ко- ординат начала системы координат создаваемой матрицы выбирают кратными величине элементов матрицы.
|
|
Для формирования цифрового трансформированного изображения каждому элементу цифрового изображения a* необходимо присвоить яркость соответствующего участка объекта, взятую с исходного циф- рового снимка. Эта операция выполняется следующим образом. По зна- чениям индексов i и j элементов матрицы a* определяются координаты X, Y центра соответствующего пикселя цифрового трансформирован- ного изображения в системе координат объекта. По координатам X i, Y i
точки объекта, соответствующей центру пикселя, по цифровой модели
рельефа определяется высота этой точки Z i. Определение значения Z i по ЦМР в виде матрицы высот выполняется методом билинейного ин- терполирования (рис. 4.8).
На рис. 4.8 DX = X i ‒ X1; DY = Y i ‒ Y1, где X1 и Y1 — координаты 1-го узла цифровой модели рельефа.
 высота точки Z i вычисляет- ся по формуле
высота точки Z i вычисляет- ся по формуле

 Z M - Z K
Z M - Z K
 |
Z i = Z K + DD DX i , (4.3.2)
где Z
= Z + Z2 - Z1 DY ; Z

 K 1 DD i
K 1 DD i
Z = Z + Z4 - Z3 DY . X

M 3 DD i O
По координатам X i, Y i, Z i и значениям элементов внутрен-
рис. 4.8
него и внешнего ориентирования снимка вычисляются координаты х, ó соответствующей точки на исходном цифровом снимке в системе координат снимка Sх óz.
вычисления производятся по формулам
é x* ù
x = x - x* ;

|
z
é X - X S ù
y*
 y = y0 - f z* , (4.3.3)
y = y0 - f z* , (4.3.3)
в которых êy* ú = AT ê Y - Y ú.
ê ú ê S ú
êë z* úû
êë Z - Z S úû
По значениям координат x, y точки снимка, которая является проекцией центра пикселя матрицы цифрового трансформированного изображения, находят ближайшие к этой точке четыре пикселя цифро- вого изображения снимка. а затем методом билинейной интерполяции, определяют значение яркости D i или цвета соответствующего пикселя матрицы цифрового трансформированного изображения. Таким же образом определяются яркости или цвет всех остальных пикселей цифрового трансформированного изображения.
Помимо метода билинейной интерполяции для формирования цифрового трансформированного изображения применяют метод «бли- жайшего соседа», в котором по координатам x, y находят пиксель сним- ка, на который проектируется точка, соответствующая центру пикселя цифрового трансформированного изображения, и значение его яркости или цвета присваивается пикселю цифрового трансформированного
изображения. Метод «ближайшего соседа» позволяет сократить время формирования цифрового трансформированного изображения по срав- нению с методом билинейной интерполяции, однако изобразительные и геометрические свойства формируемого цифрового изображения при этом ухудшаются.
Если превышения точек на участке местности, изображенной на снимке, незначительны, при создании цифрового трансформирован- ного изображения значения высот точек местности, соответствующих центрам пикселей трансформированного изображения, принимаются равными среднему значению высоты участка местности. в этом случае нет необходимости в создании цифровой модели рельефа местности, так как трансформированное цифровое изображение представляет собой центральную проекцию исходного снимка на горизонтальную пло- скость, расположенную на высоте Z, равной среднему значению высоты участка местности. Такой метод трансформирования допустим в случае, если ошибки в положении точек на трансформированном изображении, вызываемые рельефом местности, не превышают допустимых значений. величины максимально допустимых значений превышений точек местности hmax относительно средней плоскости, при которых ошибки
в положении точек на трансформированном изображении не будут пре-
вышать установленного допуска DRmax, можно определить по формуле
h = f DR ,

(4.3.4)
max r max
где f — фокусное расстояние съёмочной камеры; r — расстояние на исходном снимке от главной точки до точки на снимке.
Как следует из формулы (4.3.4) величина ошибки DRmax прямо пропорциональна значению r, поэтому при определении hmax измеряет- ся значение r до наиболее удаленной от главной точки снимка точки, участвующей в формировании трансформированного изображения. Следует отметить, что формулы (4.3.4) используют только в случае, если
трансформирование выполняется по снимкам, углы наклона которых не превышают 3–5°.
аналогичным образом можно определить величину допустимой ошибки DZmax определения высот точек местности, соответствующих центрам пикселей трансформированного изображения, по цифровой модели рельефа:
DZ = f DR .

(4.3.5)
max r max
в случае, если трансформирование снимков выполняется с целью создания или обновления карт и планов значение DRmax вы- бирается равным 0,3 мм на карте или плане, то есть DRmax = M·0,3 мм, где М — знаменатель масштаба создаваемой карты.
При создании цифровых трансформированных изображений мест- ности в проекции карты, плановые координаты узлов цифровой модели рельефа определяют в системе координат карты. в России топографи- ческие карты создаются в проекции Гаусса–Крюгера в государствен- ных системах координат СК 42; СК 63 и СК 95 или местных системах координат. высоты узлов цифровой модели рельефа задают равными геодезическим высотам H этих узлов относительно поверхности рефе- ренц-эллипсоида.
По значениям координат узлов X, Y в государственной системе координат вычисляют значения геодезической широты В и долготы L узлов цифровой модели рельефа, а затем по величинам B, L и H — координаты узлов Xгц, Yгц и Zгц в геоцентрической системе координат. Эти преобразования подробно изложены в курсах высшей геодезии и математической картографии.
в остальном процесс цифрового трансформирования аналогичен процессу создания цифрового ортофотоизображения. Необходимо толь- ко отметить, что элементы внешнего ориентирования снимка, в этом случае, должны быть определены в геоцентрической системе координат. вместо геоцентрической системы координат можно использовать топо- центрическую систему координат OтцXтцYтцZтц. Начало топоцентрической системы координат обычно выбирают в середине обрабатываемого участка местности. Ось Xтц топоцентрической системы координат лежит в плоскости меридиана, проходящего через начало системы координат. Ось Zтц совпадает с нормалью к поверхности референц-эллипсоида в начале системы координат, а ось Yтц дополняет систему до правой. При использовании топоцентрической системы координат элементы внеш- него ориентирования исходного снимка должны быть определены в этой системе координат.









