§4.2. методы цифрового трансформирования снимков
Цифровое трансформирование снимков, как уже отмечалось, выполняется с целью получения цифрового изображения объекта в заданной проекции по исходному снимку объекта. На рис. 4.1 при-
|
ведена классификация методов цифрового трансформирования снимков.
| |||||||||||
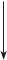
При цифровом трансформи- ровании снимка сначала задают пустую (нулевую) матрицу, со- ответствующую трансформи- рованному снимку, т.е. каждый элемент которой равен нулю. Задача заключается в том, чтобы перенести яркости d ij с исходного снимка на трансформированный
снимок. При этом может быть два подхода, так называемое прямое и обратное трансформи- рование (рис. 4.2).
Картографическая проекция
 |
рис. 4.1
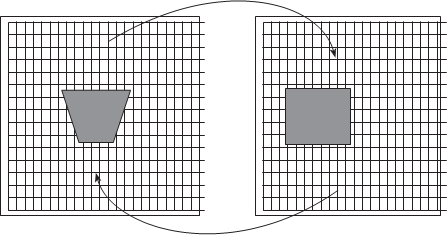
П р я м о е т р а н с ф о р - м и р о в а н и е выполняется следующим образом. Для каж- дого пикселя исходного снимка
Исходный снимок
Прямое трансформирование
d →
Трансформированный снимок
d →
Обратное трансформирование
рис. 4.2
с координатами x, y вычисляют соответствующие координаты транс- формированного снимка
xT = f(x, y); yT = f(x, y), (4.2.1)
по которым переносят яркость d с исходного на трансформированный снимок (см. рис. 4.2).
| |||||||||||||||||
Очевидно, что координаты xT и yT в результате вычислений по- лучаются дробными (вещественными) числами, например, xT=151,3 и yT=20,7, а координаты матрицы цифрового трансформированного сним- ка являются целыми числами
( xT = 1, 2, …, n, yT = 1, 2, …, m).
j j
в результате пиксель исходного снимка не совпадает в точности с каким-либо центром пикселя трансформированного снимка. Он как бы накрывает 4 пикселя трансформированного сним- ка (рис. 4.3). Здесь пунктиром
показано положение пикселя, рис. 4.3
|
которое он должен занимать в матрице трансформированного снимка согласно вычисленным координатам. встает вопрос, какому из четырех пикселей матрицы трансформированного снимка присвоить яркость d ij с исходного снимка? Один из возможных вариантов, это распределить соответствующую яркость между четырьмя пикселями пропорциональ- но площади покрытия каждого пикселя трансформированного снимка исходным пикселем. Таким образом, яркость любого пикселя транс- формированного снимка dT будет складываться из приращений соответ-
ствующих яркостей ∆d ij пикселей исходного снимка, т.е. d T = åDd , где
1
k — число пикселей исходного снимка, покрывающих данный пиксель трансформированного снимка.
О бр а т н о е т р а н с ф ор м и р о в а н и е выполняется по обрат- ным (4.2.1) формулам:
x = f(xT , yT );
y = f(xT , yT ),
(4.2.2)
т.е. задаваясь координатами xT, yT какого-либо пикселя на трансформи- рованном изображении, по формулам (4.2.2) вычисляют координаты соответствующего пикселя на исходном снимке x, y, по которым бе- рется яркость d и переносится на трансформированное изображение. Здесь также возникает проблема вычисления яркости d на исходном снимке из-за того, что координаты x, y получаются дробными числами. вопрос решается следующим образом. Можно округлить координаты x, y до целых чисел j и i соответственно (например, x=150,3; y=21,7, тогда j=150, i=22), взять из матрицы исходного снимка яркость d ij и присвоить ее соответствующему пикселю трансформированного снимка. Такой
метод называется методом «б л и ж а й ш е г о с о с е д а». Однако этот метод приводит к некоторому снижению фотометрического и геометри- ческого качества трансформированного снимка. Другой подход связан с применением методов интерполирования яркостей между соседними пикселями. Чаще всего применяется метод д в о й н о г о л и н е й н о г о и н т е р п о л и р о в а н и я, суть которого будет рассмотрена ниже.
вид функций (4.2.1) и (4.2.2) зависит от геометрии построения ис- ходного снимка и от вида проекции, в которую будет трансформиро- ваться данный снимок. Для снимков, представляющих собой централь- ную проекцию, в качестве таких функций чаще используют прямые и
обратные уравнения коллинеарности, связывающие координаты точки объекта, снимка и центр проекции.
На практике чаще используют обратное трансформирование, так как при прямом трансформировании могут возникнуть разрывы в изо- бражении (пустые пиксели на трансформированном снимке), более сложно решается вопрос определения и заполнения мертвых зон, а также метод требует больших затрат машинного времени.
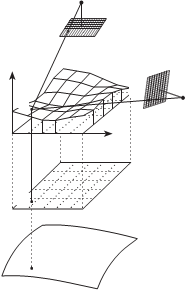
К о м б ини р о в а нн о е т р а н с ф о р м и р о в а ни е представля- ет собой комбинацию из прямого и обратного методов трансформирова- ния. Применяется как один из методов определения и заполнения мерт- вых зон на ортофотоснимке. в качестве проекции трансформирования обычно используют ортогональную или центральную проекции. Рис. 4.4 иллюстрирует суть трансформирования исходного снимка в заданную проекцию. Для этого для любой точки местности М, изобразившейся в точке m на исходном снимке, вычисляется ее положение (координаты) в заданной проекции M0 или MЦ, куда переносится соответствующая яркость с исходного снимка. Таким образом получается изображение
местности в ортогональной или центральной проекции.
Следует отметить, что цен- тральная проекция, как проекция
трансформирования применяет- ся для получения перспектив- ных изображений на данный
Исходный
mснимок
участок местности, задаваясь Z
соответствующими элементами внешнего ориентирования но- М вого снимка. Кроме того, этот способ трансформирования ши- O роко применяется для получения идеальных стереопар снимков (с
ЦМР
X
Мц
Новый снимок (центральная проекция)
углами наклона равными нулю), необходимых для облегчения процесса стереонаблюдений и измерений. При этом в качестве системы координат объекта OXYZ используется фотограм- метрическая система координат
Ортогональная
Мо проекция
Картографическая проекция
Мк
рис. 4.4
и соответственно элементы взаимного ориентирования пары исходных снимков.
в случае трансформирования мелкомасштабных снимков на боль- шие территории следует использовать картографическую проекцию, например, проекцию Гаусса–Крюгера, учитывающую кривизну Земли, или UTM. Цифровая модель рельефа задается как правило в одной из геоцентрических или топоцентрических систем координат.
Ниже более подробно рассматриваются основные методы транс- формирования снимков, как наиболее часто используемые, проблемы, возникающие при этом и способы их решения.