§3.5. Построение и уравнивание маршрутной и блочной фототриангуляции по методу связок
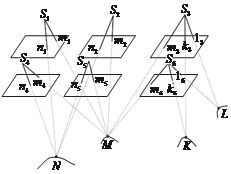 С геометрической точки зрения сеть фототриангуляции по методу связок строится под условием пересечения соответ- ственных проектирующих лучей в точках объекта, а для каждой связки проектирующих лучей – в соответствующем центре про- екции (рис. 3.9).
С геометрической точки зрения сеть фототриангуляции по методу связок строится под условием пересечения соответ- ственных проектирующих лучей в точках объекта, а для каждой связки проектирующих лучей – в соответствующем центре про- екции (рис. 3.9).
Математической основой
рис. 3.9
метода связок являются извест- ные уравнения коллинеарности,
которые составляются для каждого изображения точки (определяемой и опорной), измеренной на снимке:
æ x* ö
x0
æ X - X
- f x* - x = 0;
 z*
z*
ö
y - f y* - y = 0,
 0 z*
0 z*
(3.5.1)
ç ÷ ç S ÷
где ç y* ÷ = AT çY - Y S ÷; x, y — координаты изображения точки мест-
ç z* ÷
çè Z - Z S ÷ø
è ø
ности, измеренной на снимке; X, Y, Z — координаты точки местности в системе координат объекта OXYZ; X S, Y S, Z S — координаты центров проекции снимка в системе координат объекта; а — матрица преобра- зования координат, элементы a ij которой являются функциями угловых элементов внешнего ориентирования снимка.
Уравнения поправок, соответствующие условным уравнениям (3.5.1), в общем случае, имеют вид:
a1dX S + a2dY S + a3dZ S + a4dw + a5da + a6dk + a7dX + a8dY + a9dZ + l x = Jx ;
b dX
+ b dY
+ b dZ
+ b dw + b da + b dk + b dX + b dY + b dZ + l
= J . (3.5.2)
1 S 2 S 3 S 4 5 6 7 8 9 y y
в случае, если в уравнения (3.5.1) входят измеренные параметры, то из уравнений поправок (3.5.2) исключаются члены, соответствующие этим параметрам. Например, в случае, если при съемке были определе- ны угловые и линейные элементы внешнего ориентирования снимка, уравнения поправок имеют вид:
a7dX + a8dY + a9dZ + l x = Jx ;
b7dX + b8dY + b9dZ + l y = Jy .
(3.5.3)
Для каждой планово-высотной опорной точки составляются урав- нения поправок
dX + l X = JX ;
dY + l Y = JY ;
dZ + l Z = JZ , (3.5.4)
в которых l X = X 0 - X ; l Y = Y 0 - Y ; l Z = Z 0 - Z ; X, Y, Z — измеренные
координаты опорной точки; X0, Y0, Z0 — приближенные значения коор- динат опорной точки.
Для плановой опорной точки составляются два первых уравнения из системы уравнений (3.5.4), а для высотной опорной точки – третье уравнение. Если с помощью системы ГНСС были определены коорди- наты центров проекций снимков S, то для каждого центра проекции составляются уравнения поправок
dX S + l Xs = JXs;
dY S + l Ys = JYs ;
dZ S + l Zs = JZs, (3.5.5)
|
|
|
в которых l Xs = X 0 - X S ; l Ys = Y 0 - Y S ; l Zs = Z 0 - Z S ; X S, Y S, Z S — из-
|
меренные координаты центров проекции снимков; X 0 , Y 0 , Z 0 — их
приближенные значения.
в случае, если при съемке с помощью навигационного комплекса, включающего инерциальную и ГНСС-системы, были определены угло- вые элементы внешнего ориентирования снимков для каждого снимка составляются уравнения поправок:
dw + lw = Jw;
da + la = Ja ;
dk + lk = Jk , (3.5.6)
в которых lw = w0 - w;
la = a0 - a;
lk = k0 - k; ω, α, κ — измеренные
значения угловых ЭвО; ω0, α0, κ0 — их приближенные значения.
Таким образом, на основании уравнений (3.5.2)–(3.5.6) составляют систему уравнений поправок
Ad+ L = V, (3.5.7)
где A — матрица (M×N) коэффициентов (частных производных) уравнений поправок; M — количество уравнений поправок (строки); N — количество неизвестных (столбцов); δ — вектор неизвестных размерностью N; L — век- тор свободных членов уравнений поправок размерностью M; V — вектор поправок в измерения (невязки уравнений поправок) размерностью M.
Структура матрицы а показана на рис. 3.10. Здесь серым цветом показаны значащие коэффициенты уравнений поправок, а остальные коэффициенты равны нулю.
Полученную таким образом систему уравнений поправок решают методом приближений по способу наименьших квадратов под условием VTPV=min, где р — диагональная матрица размерностью M×M весов измерений,
æ p1 0 0 0 0 ö
|
|
|
|
ç 0 0 0 ÷
P = ç 0 0 0 0 ÷. (3.5.8 )
|
|
ç 0 0 0 0 ÷
|
|
ç 0 0 0 0 p M ÷
веса измерений p i можно вычислить по формуле:
|
|
|
p = 1 , (3.5.9 )
i
где m i — средняя квадратическая ошибка измерения i.
Для решения уравнений поправок по способу наименьших квадра- тов составляют нормальные уравнения вида:
AT PAd+ AT PL = 0
или
AN d+ LN = 0, (3.5.10 )
где AN — матрица коэффициентов нормальных уравнений размер- ностью N×N; LN — вектор свободных членов нормальных уравнений размерностью N.
Неизвестные (шесть элементов внешнего ориентирования для каждого сним- ка и три координаты для каждой точки)
δX S1 δY S1 δZ S1
δX S2 δY S2 δZ S2
δX1 δY1 δX2 δY2 δX3 δY3 δX4 δY4 δX5 δY5 δX6 δY6
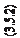 δω1 δφ1 δκ1
δω1 δφ1 δκ1
δω2 δφ2 δκ2 ···
δZ1
δZ2
δZ3
δZ4
δZ5
δZ6 ···
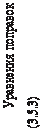 | ||
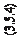 | ||
|
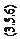
 рис. 3.10
рис. 3.10
или
Решение уравнений (3.5.10 ) получается как:
d= -(AN )-1 LN
(3.5.11)
d= QLN , (3.5.12)
где Q — обратная матрица нормальных уравнений.
Таким образом получают поправки к приближенным значениям не- известных, на величины которых последние уточняются. Затем процесс составления и решения уравнений поправок повторяется. Так поступают до тех пор пока поправки к приближенным значениям неизвестных не станут пренебрегаемо малыми величинами. в последнем приближении делают оценку точности, вычисляя средние квадратические ошибки неизвестных:
 m j =m Q jj , (3.5.13 )
m j =m Q jj , (3.5.13 )
где Q jj — диагональные элементы обратной матрицы нормальных уравнений; μ — средняя квадратическая ошибка единицы веса, которая вычисляется по формуле
 m= (3.5.14)
m= (3.5.14)
в результате находят уравненные значения элементов внешнего ориентирования снимков сети и координаты точек сети в системе ко- ординат объекта.
Общее количество неизвестных, определяемых при построении и уравнивании блочной сети, можно определить по формуле
N= 6n + 3k, (3.5.15)
где n — количество снимков в сети; k — количество определяемых точек (включая опорные геодезические точки).
Общее количество уравнений поправок можно определить по формуле
M= 2m + 3c + 2i + l + 3s + 3j, (3.5.16)
где m — общее количество измеренных на снимках точек; c — коли- чество планово-высотных опорных точек; i — количество плановых опорных точек; l — количество высотных опорных точек; s — коли- чество центров проекций снимков, координаты которых были опре-
делены с помощью системы ГНСС; j — количество снимков, угловые элементы которых были определены.
Рассчитаем величины M и N для блочной сети, изображенной на рис. 3.11, построенной по двум маршрутам, в каждом из которых четыре снимка, с использовани- ем в качестве опорной информа- ции координат опорных точек и центров проекции снимков.
Для блочной сети, изо- браженной на рис. 3.11, n=8, k=20, поэтому N=6×8+3×20=108.
| 2 | 4 | 4 | 2 |
| |||
| 2 | 3 | 3 | 2 | ||||
| 2 | 4 | 4 | 2 | ||||
| 2 | 3 | 3 | 2 | ||||
| 6 | 8 | 8 | 6 | ||||
| 4 | 6 | 6 | 4 | ||||
| 2 | 4 | 4 | 2 | ||||
| 2 | 3 | 3 | 2 | ||||
| 2 | 4 | 4 | 2 | ||||
| 2 | 3 | 3 | 2 |
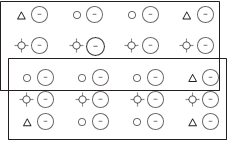 — главная точка снимка; — точка сети;
— главная точка снимка; — точка сети;


|
— планово-высотная точка; 2 — количество точек, измеренных на снимках (в числителе — коли- чество точек, измеренных на стереокомпараторе или аналитической стереофотограмметрической системе, а в знаменателе — количество точек, измеренных на
цифровой фотограмметрической системе)
рис. 3.11
Из рис. 3.11 следует, что m=72, если снимки измерялись на стереоком- параторе или аналитическом стереофотограмметрическом приборе и m=60, если снимки измерялись на цифровой фотограмметрической системе c=5, а S=8. Следовательно, M=2×72+3×5+3×8=183, если снимки измерялись на стереокомпараторе или аналитической стереофотограм- метрической системе, и M=2×60+3×5+3×8=159, если снимки измерялись на цифровой фотограмметрической системе. в нашем случае M˃N, значит система имеет решение.









