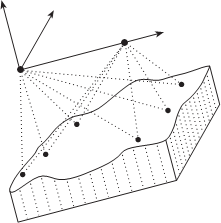
Построение модели маршрута
Производится путем последовательного присоединения каж- дой последующей к первой модели. Этот процесс выполняется в два этапа. Сначала определяют элементы внешнего ориентирова- ния присоединяемой модели в системе координат модели маршрута X M 0i , Y M 0i , Z M 0i , wMi , aMi , kMi , t i , где i — номер присоединяемой модели (i = 2, 3, …, n).
Для определения элементов внешнего ориентирования присо- единяемой модели для каждой связующей точки составляют систему уравнений
æ X M
ç
ö
0 i ÷
æ X Mi ö
ç ÷
æ X M ö
ç ÷
|
ç Y M
÷ + AMi ç
Y Mi
÷t i - ç Y M
÷ = 0, (3.2.1)
ç Z ÷
ç Z Mi ÷
ç Z M ÷
è M 0i ø
è ø è ø
в которой X M, Y M, Z M — координаты связующей точки в системе коорди- нат модели маршрута; X Mi, Y Mi, Z Mi — ее координаты в системе координат i–й модели.
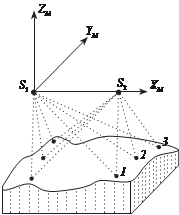
Для определения элементов внешнего ориентирования модели не- обходимо не менее трех связующих точек. в качестве связующей точки обязательно используется центр проекции S общего для двух соседних моделей снимка.
После определения элементов внешнего ориентирования модели определяют координаты точек присоединяемой модели в системе коор- динат модели маршрута по формулам
æ X M ö
ç ÷
æ X M
ç
ö
0 i ÷
æ X Mi ö
ç ÷
ç Y M
÷ = ç Y M 0 i
÷ + AMi ç
Y Mi
÷t i . (3.2.2)
ç Z M ÷ ç Z ÷
ç Z Mi ÷
è ø è
M 0i ø è ø
Необходимо отметить, что координаты связующих точек и общего для соседних моделей центра проекции снимка S в системе координат
 Z Mi
Z Mi
Y Mi
S3 X Mi
 S2
S2
3 i
2 i
1 i
Z M
Y M
S1 S2
рис. 3.3
|
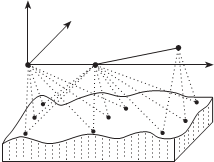
модели маршрута определяются дважды (по двум соседним мо- делям). Разности этих координат
3
∆ X, ∆Y, ∆Z служат критерием
X M точности построения модели маршрута и позволяют выявить
3 грубые измерения.
1 2 в качестве окончательно- го значения координат точек
модели маршрута берутся их
рис. 3.4
средние значения из двух опре- делений.
Рис. 3.3 и 3.4 иллюстрируют процесс построения модели маршрута .
внешнее ориентирование модели маршрута
Производится по опорным точкам в два этапа. Сначала определяют элементы внешнего ориентирования модели маршрута X0, Y0, Z0, ωM, αM, κM, t в системе координат объекта OXYZ. Этот процесс полностью аналогичен процессу внешнего ориентирования фотограмметрической модели, построенной по стереопаре снимков. После определения элемен- тов внешнего ориентирования модели маршрута вычисляют координаты точек модели маршрута в системе координат объекта:
æ X ö æ X 0 ö æ X M ö
ç Y ÷ = ç Y0 ÷ + AM ç Y M ÷t. (3.2.3)
ç ÷ ç ÷ ç ÷
çè Z ÷ø
çè Z0 ÷ø
çè Z M ÷ø
устранение систематических искажений маршрутной сети по опорным точкам
вследствие неполного учета систематических ошибок снимка, вы- зываемых дисторсией объектива, атмосферной рефракцией и другими причинами, координаты точек сети, определенные по формулам (1.2.3), могут содержать систематические ошибки, которые накапливаются от модели к модели.
Систематические искажения сети маршрутной фототриангуляции можно описать с помощью полиномов, например, полиномов 2-го по- рядка:
ì X = X + A + A X + A Y + A XY + A X 2 ;
ï è 0 1 2 3 4
í Y = Y + B + B X + B Y + A XY + B X 2 ;
(3.2.4)
è 0 1 2 3 4
ï Z = Z + C + C X + C Y + C XY + C X 2 ,
î è 0 1 2 3 4
где A i, B i, C i — коэффициенты полиномов; X, Y, Z — координаты точек сети, определенные в результате внешнего ориентирования модели маршрута; Xи, Yи, Zи — координаты точек сети, исправленные за влияние систематических ошибок.
Для определения коэффициентов полиномов необходимо не менее пяти планово-высотных опорных точек, расположенных по схеме, пред- ставленной на рис. 3.5, так как каждая опорная точка позволяет соста- вить три линейных уравнения с 15-ю неизвестными коэффициентами полиномов A i, B i, C i:
ì X + A + A X + A Y + A XY + A X 2 - X = J ;
ï 0 1 2 3 4 è x
í Y + B + B X + B Y + A XY + B X 2 - Y = J ;
(3.2.5)
0 1 2 3 4 è y
ï Z + C + C X + C Y + C XY + C X 2 - Z = J ,
î 0 1 2 3 4 è z
где Xи, Yи, Zи — геодезические координаты опорной точки в си- стеме координат объекта.
в результате решения си- стемы уравнений (3.2.5) находят
Y


 O X
O X
рис. 3. 5
значения коэффициентов полиномов A i, B i, C i. Если опорных точек больше пяти, то решение производят методом наименьших квадратов. По координатам точек сети X, Y, Z и значениям коэффициентов A i, B i, C i находят по формулам (3.2.4), исправленные за систематические иска- жения координаты точек сети Xи, Yи, Zи.
Y* Y
O
κM
рис. 3.6
Следует отметить, что в
 случае если направление оси X M
случае если направление оси X M
системы координат модели
X* маршрута не совпадает с осью X системы координат объекта (рис. 3.6), перед выполнением
X процесса исключения система- тических ошибок необходимо предварительно перевычислить
координаты X, Y, Z опорных и определенных точек сети из системы координат объекта во вспомогательную систему координат объекта
|
OX*Y*Z*, ось X* которой параллельна оси X
в системе координат объекта.
системы координат модели
вычисления производят по формулам
æ X * ö
ç Y * ÷ = AT
æ X ö
ç Y ÷. (3.2.6)
ç ÷ kM ç ÷
çè Z * ÷ø
çè Z ÷ø
|
Затем производят устранение систематических искажений коорди- нат точек сети по методике, описанной выше и перевычисляют исправ-
ленные значения координат точек сети объекта по формулам
X *, Y *, Z * в систему координат
æ X ö æ X * ö
|
è
|
= A
ç è ÷
Y * .
(3.2.7)
ç è ÷ kM ç è ÷
ç Z ÷ ç Z * ÷
è è ø è è ø
в формулах (3.2.6) и (3.2.7) матрицы преобразования координат и имеют вид:
æ cos kM
-sin kM 0 ö
æ cos kM
sin kM 0 ö
|
|
|
A = ç sin kM
cos kM 0 ÷;
AT
|
M
= ç - ssin kM
cos kM 0 ÷,
|
|
|
ç 0 0 1 ÷ø ç 0 0 1 ÷ø
здесь κM — угол разворота системы координат модели.
§3.3. Блочная фототриангуляция
по методу независимых маршрутов







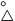
|
Блочная фототриангуляция по методу независимых марш- рутов выполняется следующим образом. Сначала строят модели маршрутов по методике, изло- женной в §3.2, а затем объеди- няют их в блочную сеть по свя- зующим точкам, расположенным в межмаршрутном перекрытии, с одновременным их внешним
 |  |  | |||



 |  |  |  | ||||
— связующая точка;
— опорная точка
рис. 3.7
ориентированием по опорным точкам (рис. 3.7).
Для объединения моделей маршрута в блочную модель с одновре- менным ее внешним ориентированием для каждой связующей точки составляют уравнения
X i - X j = 0;
Y i - Y j = 0;
Z i - Z j = 0, (3.3.1)
в которых X i, Y i, Z i и X j, Y j, Z j — координаты связующей точки в системе координат объекта, определенные соответственно по i-й и j-й моделям.
Значения X i, Y i, Z i и X j, Y j, Z j определяются по формулам:
æ X i ö æ X 0i ö
æ X Mi ö
æ X j ö æ X 0 j ö
æ X Mj ö
ç Y ÷ = ç Y
÷ + A ç Y ÷t ;
ç Y ÷ = ç Y
÷ + A ç Y ÷t .
ç i ÷
ç 0i ÷
Mi ç Mi ÷ i
ç j ÷
ç 0 j ÷
Mj ç Mj ÷ j
çè Z i ÷ø
çè Z0i ÷ø
çè Z Mi ø÷
çè Z j ÷ø
çè Z0 j ÷ø
èç Z Mj ÷ø
Таким образом в уравнениях (3.3.1) неизвестными являются эле- менты внешнего ориентирования i и j моделей.
Для каждой опорной точки (планово-высотной), измеренной в маршруте, составляют уравнения
æ X 0i ö æ X Mi ö æ X ö
ç Y0i ÷ + AMi ç Y Mi ÷t i - ç Y ÷ = 0, (3.3.2)
ç ÷ ç ÷ ç ÷
ç Z0i ÷ ç Z Mi ÷ ç Z ÷
è ø è ø è ø
где i — номер модели; X, Y, Z — координаты опорной точки в системе координат объекта.
Уравнения поправок соответствующие уравнениям (3.3.1) и (3.3.2) имеют вид:
a1dX 0i + a2dY0i + a3dZ0i + a4dwMi + a5daMi + a6dkMi +
+ a7dt i + a8dX oj + a9dY oj + a10dZ oj +
+ a11dwMj + a12daMj + a13dkMj + a14dt j + l x = Jx ;
b1dX 0i + b2dY0i + b3dZ0i + b4dwMi + b5daMi + b6dkMi +
+ b7dt i + b8dX oj + b9dY oj + b10dZ oj +
+ b11dwMj + b12daMj + b13dkMj + b14dt j + l y = Jy ;
c1dX 0i + c2dY0i + c3dZ0i + c4dwMi + c5daMi + c6dkMi +
+ c7dt i + c8dX o j + c9dY oj + c10dZ o oj +
+ c11dwMj + c12daMj + c13dkMj + c14dt j + l z = Jz ;
a1dX 0i + a2dY0i + a3dZ0i + a4dwMi + a5daMi + a6dkMi + a7dt i + l x = Jx ; b1dX 0i + b2dY0i + b3dZ0i + b4dwMi + b5daMi + b6dkMi + b7dt i + l y = Jy ; c1dX 0i + c2dY0i + c3dZ0i + c4dwMi + c5daMi + c6dkMi + c7dt i + l z = Jz .
(3.3.3)
(3.3.4)
Для плановой опорной точки (X, Y) составляются только два первых уравнения поправок (3.3.4), а для высотной опорной точки (Z) только третье уравнение. в результате совместного решения системы уравне- ний поправок (3.3.3) и (3.3.4) по методу наименьших квадратов находят значения элементов внешнего ориентирования всех моделей маршрутов в системе координат объекта.
Затем вычисляют координаты точек блочной сети в системе коор- динат объекта в каждом маршруте:
æ X ö æ X 0i ö æ X Mi ö
ç Y ÷ = ç Y0i ÷ + AMi ç Y Mi ÷t i .. (3.3.5)
ç ÷ ç ÷ ç ÷
çè Z ÷ø
çè Z0i ÷ø
çè Z Mi ÷ø
Координаты межмаршрутных связующих точек в этом случае вы- числяются дважды. За окончательное значение берется среднее из них. Общее количество неизвестных, определяемых в результате решения системы уравнений поправок в этом методе блочной фототриангуляции, определяется по формуле
N= 7n, (3.3.6)
где n — количество маршрутов.
Общее количество уравнений поправок определяется по формуле
M = 3m + 3k + 2i + l, (3.3.7)
где m — количество межмаршрутных связующих точек; k — коли- чество планово-высотных опорных точек, измеренных в маршрутах; i и l — количество плановых и высотных опорных точек, измеренных в маршрутах.
Для сети, изображенной на рис. 3.7
N=7×3=21; М=3×14+3×8=42+24=66,
так как m=14 (две опорные точки, расположенные в межмаршрут-ном перекрытии, используются как связующие), а k=8 (две опорные точки измерены в двух соседних маршрутах).








