§2.12. определение элементов внешнего ориентирования снимков стереопары
По элементам внешнего ориентирования модели и элементам взаимного ориентирования можно определить элементы внешнего
ориентирования снимков стереопары. линейные элементы внешнего ориентирования снимков определяют по формулам:
æ X S ö
æ X ö
æ X S ö
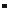
ç i ÷
|
|
ç Y S ÷ = ç
ç ÷
0 ÷
Y0 ÷
ç
+ AM ç Y S
ç Mi
i ÷
÷t, (2.12.1)
÷
ç Z S ÷
ç Z0 ÷
ç Z ÷
è i ø è ø
è S M i ø
в которых X S ,Y S , Z S — координаты центра проекции i-го снимка
Mi Mi Mi
стереопары в системе координат модели.
Угловые элементы внешнего ориентирования снимков wi, ai, κi
определяют в следующей последовательности:
1) получают матрицу преобразования координат i-го снимка
Ai = AM A¢i , (2.12.2)
где аМ — матрица, в которой элементы a ij вычисляют по угловым эле-
ментам внешнего ориентирования модели wМ, aМ, κМ; A¢i — матрица,
в которой элементы a ij вычисляют по угловым элементам взаимного ориентирования i-го снимка w¢i , a¢i , k¢i ;
2) по элементам a ij матрицы Ai вычисляют угловые элементы внеш- него ориентирования i-го снимка стереопары
w = arctg æ - a23 ö;
a = arcsin (a );
k = arctg æ - a12 ö.
i ç a ÷ i
13 i
ç a ÷
è 33 ø è 11 ø
§2.13. Точность определения координат точек объекта по стереопаре плановых снимков
Так как на стереопаре плановых снимков углы наклона снимков не превышают 1–3°, а базис фотографирования практически горизон- тален, для оценки точности определения координат точек местности по стереопаре снимков воспользуемся формулами связи координат точек местности и координат их изображений на стереопаре снимков идеаль- ного случая съемки (2.5.4):
X =- Z x; Y =- Z y; Z =- B f.
f f p
Сначала получим формулу для вычисления средней квадратиче- ской погрешности определения высоты точки Z местности по стереопаре
снимков. Для этого продифференцируем третью формулу выражения (2.5.4) по аргументу р:
¶Z = B f = - Z .
¶p p2 p
Заменим величину р на b — базис в масштабе снимка (рис. 2.17), в этом случае
¶Z =- Z .
¶p b
Перейдя к средним квадратическим погрешностям, получим:
m = Z m . (2.13.1)
Z b p
Для вычисления средних квадратических погрешностей определе- ния координат Х и Y точки местности по стереопаре снимков, продиф- ференцируем первые две формулы выражения (2.5.4) по аргументам x, y и Z и перейдем к средним квадратическим погрешностям. в результате получим:
m X =
m Y =
» Z m ;
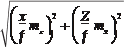f x
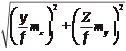
» Z m .
f y
(2.13.2)
в качестве примера вычислим величины средних квадратических погрешностей m X, m Y и m Z определения координат точек местности по стереопаре снимков, полученных с высоты 2000 м с продольным перекрытием 60%, полноформатной цифровой аэрофотокамерой DMC II 250, фирмы Z/I.
аэрофотокамера DMC II 250 имеет объектив с фокусным расстоянием 112 мм и матри- цу, имеющую размеры по оси x — 14656 пикселей, а по оси y — 17216 пикселей (размер пикселя 5,6 мкм). Будем счи- тать, что на стереопаре снимков
рис. 2.17
точки были измерены с погрешностями m x = m y = 0,5 пиксель = 2,8 мкм и m p = 0,3 пиксель = 1,7 мкм.
При продольном перекрытии снимков стереопары 60% и длине
стороны кадра, направленного вдоль направления полета, равного 14656 пикселей или 82,1 мм базис в масштабе снимка будет равен
b = 82,1 ìì (100% - 60%) = 32,8 ìì.
100%
Средние квадратические погрешности определения координат точки местности, вычисленные по формулам (2.13.1) и (2.13.2) для на- шего примера будут равны:
m = Z m
X f x
m = Z m
= 2000 ì 0, 0028 ìì = 0, 05 ì;
112 ìì
= 2000 ì 0, 0028 ìì = 0, 05 ì;
Y f y
112 ìì
m = Z m
Z b p
= 2000 ì 0, 0017 ìì = 0,10 ì.
32,8 ìì
|
Глава 3
 |
Пространственная фототриангуляция