§2.9. построение фотограмметрической модели
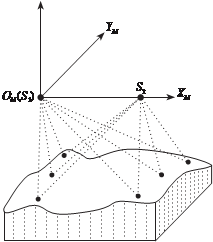 Z M Построение фотограмметри- ческой модели заключается в опре- делении координат точек объекта по измеренным на стереопаре снимков координатам их изобра- жений в системе координат модели
Z M Построение фотограмметри- ческой модели заключается в опре- делении координат точек объекта по измеренным на стереопаре снимков координатам их изобра- жений в системе координат модели
О Х Y Z (рис. 2.15).
М М M M
Определение координат точек модели производится по форму- лам прямой фотограмметриче- ской засечки (см. §2.4). При этом координаты центра проекции S принимаются произвольными
(обычно X S = Y S = Z S = 0 ). Также
рис. 2.15
1 1 1
произвольно (но не равно нулю)
выбирается величина В Х. в боль- шинстве случаев практики B X = bm,
где b — базис фотографирования в масштабе снимка; m — знаменатель
масштаба снимка.
Остальные значения элементов внешнего ориентирования опреде- ляют по восьми параметрам b y , b z , w1¢, a1¢, k1¢, w¢2 , a¢2 , k¢2 , пять из которых являются элементами взаимного ориентирования, а три определяют
ориентацию системы координат модели, при этом
B Y = B Xb y ;
w1 = w1¢;
a1 = a¢;
k1 = k1¢;
B Z = B Xb y ;
w2 = w¢2 ;
a2 = a¢2 ;
k2 = k¢2.
Например, если были определены элементы взаимного ориентиро- вания a1¢, k1¢, w¢2 , a¢2 , k¢2 и при этом величины параметров b y, b z, w1¢ были приняты равными нулю (b y=b z= w1¢ =0), то B Y=B Z=0, w1=0, a1= a1¢ , κ1= k1¢ ,
w2= w¢2 , a2= a¢2 , κ2= k¢2.
Если были определены элементы взаимного ориентирования
b y , b z , w¢2 , a¢2 , k¢2, а величины параметров w1¢, a1¢, k1¢
ными нулю ( w1¢ = a1¢ = k1¢ = 0 ), то
были приняты рав-
B Y = B Xb y ;
w1 = 0;
a1 = 0;
k1 = 0;
B Z = B Xb z ;
w2 = w¢2 ;
a2 = a¢2 ;
k2 = k¢2.
§2.10. внешнее ориентирование модели.
Элементы внешнего ориентирования модели
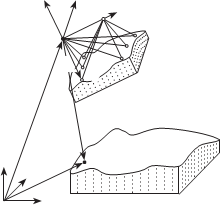
На рис. 2.16 показаны эле-
менты внешнего ориентирования модели, где О Х Y Z — система
Z M Y M
 S2 X M
S2 X M
М М M M
координат фотограмметрической
O (S )
|
M
модели; OXYZ — система коор-
|
|
динат объекта; А — точка объек- R M
та; А М — точка фотограмметри-
|
ческой модели, соответствующая R0
0 R A R
и R определяют положение на-
чала системы координат модели Z R A
О Х Y Z и точки А местности Y A
М М M M
в системе координат объекта O X
OXYZ; вектор R M = O M A M опре-
рис. 2.16
деляет положение точки А М в системе координат фотограмметрической модели О МХ МY MZ M.
Из рис. 2.16 следует, что
R A = R0 + R. (2.10.1)
Очевидно, что векторы R M и R связаны между собой следующим
соотношением:
R = AM R Mt, (2.10.2)
где аМ — матрица преобразования координат, элементы a ij которой являются функциями углов wМ, aМ, κМ, определяющих ориентацию системы координат модели относительно системы координат объекта; t — знаменатель масштаба модели.
С учетом (2.10.2) выраж ение (2.10.1)имеет вид:
R A = R0 + AM R Mt. (2.10.3)
в координатной форме выражение (2.10.3) имеет вид:
æ X ö æ X 0 ö
æ X M ö
ç Y ÷ = ç Y
÷ + A ç Y ÷t
(2.10.4)
ç ÷ ç 0 ÷
M ç M ÷
ç Z ÷ ç Z0 ÷ ç Z M ÷
или
è ø è ø è ø
|
X = X 0 + (a11 X M + a12Y M + a13Z M )t;ü Y = Y + (a X + a Y + a Z )t; ï
(2.10.5)
Z = Z + (a X + a Y + a Z )t. ï
0 331 M 32 M 33 M þ
Здесь X, Y, Z — координаты точки объекта в системе координат объекта; X M, Y M, Z M — координаты соответствующей точки модели в системе координат фотограмметрической модели; X0, Y0, Z0 — коорди- наты начала системы координат модели в системе координат объекта.
Семь параметров X 0 ,Y0 , Z0 , wM , aM , kM ,t
внешнего ориентирования модели.
называют элементами








