§2.4. Формулы связи координат точек местности и их изображений на стереопаре снимков (прямая фотограмметрическая засечка)

Дата: 2025-06-02; Просмотры: 17
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

На рис. 2.12 показана стереопара снимков Р1 и Р2, на которых точка местности М изобразилась соответственно в точках m1 и m2. Будем счи- тать, что элементы внутреннего и внешнего ориентирования съемочных камер, с помощью которых были получены снимки, известны. выведем формулы связи координат точек местности и координат их изображений

на стереопаре снимков.

Из рис. 2.12 следует, что векторы

R M и

1

R S определяют соответ-

ственно положение точка местности М и центра проекции S1 снимка Р1

относительно начала системы координат объекта OXYZ. вектор B опре-

S2

деляет положение центра про-

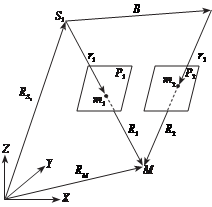екции S2 снимка Р2 относительно

центра прое_к_ ции S1. векторы

S M = R

S1m1 = r1 и

1 1 определяют

положение точек m1 и М отно-

сительно ц е н _тра прое к ц и и S 1.

2 2 2

векторы S m = r_ и S M = R

2 2

определяют положение точек m2 и М относительно центра про- екции S2, следовательно

 

1

R M = R S + R1. (2.4.1) O

рис. 2.12

Так как векторы R1

 

где N — скаляр.

и r

 

1

коллинеарны, то

 

R1 = N r1, (2.4.2)

С учетом (2.4.2) выражение (2.4.1) будет иметь вид

  

1

R M = R S + N r1. (2.4.3)

в координатной форме выражение (2.4.3) будет иметь вид

æ X ö

æ X S ö

æ X ¢ ö

ç Y ÷

ç

= ç Y S

1 ÷

÷ + N

1

Y1¢

, (2.4.4)

÷
ç

ç ÷ ç 1 ÷ ç ÷

ç Z ÷

ç Z ÷

ç Z1¢ ÷

 

¢ ¢ ¢

è ø è S1 ø  è ø

где

X1, Y1, Z1

— координаты вектора

r1 в системе координат объекта

OXYZ,

æ X1¢ ö æ x1 - x01 ö

ç Y1¢ ÷ = A1 ç y1 - y01 ÷.

ç ÷ ç ÷

ç Z1¢ ÷ ç -f1 ÷

è ø è ø

Найдем значениеN, входящее в выражение (2.4.4). Из рис. 2.12 следует, что R2 = R1 - B или с учетом (2.4.2)

  

R2 = N r1 - B. (2.4.5)

Так как векторы R2

 коллинеарны, то их векторное произве-

r
и
2

дение  

R2 ´ r2 = 0. (2.4.6)

С учетом (2.4.5) выражение (2.4.6) можно представить в виде

(N r - )´ r = N (r ´ r ) - (  ´ r ) = 0

 

или

1 B 2 1 2 B 2

   

N (r1 ´ r2 ) = (B ´ r2 ). (2.4.7) выражение (2.4.7) можно представить в виде:

     

i j k i j k

N X1¢

Y1¢

Z1¢ = B X

B Y B Z

или

X 2¢

Y2¢

Z2¢

X 2¢

Y2¢

Z2¢

N é(Y ¢Z ¢ - Y ¢Z ¢)  - ( X ¢Z ¢ - X ¢Z ¢)  + ( X ¢Y ¢ - X ¢Y ¢) ù =

ë 1 2 2 1 i 1 2 2 1 j 1 2 2 1 k û

= ( B Z ¢ - B Y ¢)  - ( B Z ¢ - B X ¢ )  + ( B Y ¢ - B X ¢ ) , (2.4.8)

 

Y 2

 

Z 2 i

X 2 Z 2 j

X 2 Y 2 k

где i , j , k — орты, совпадающие с осями координат X, Y, Z системы коор- динат объекта OXYZ; B X , B Y , B Z , X1¢, Y1¢, Z1¢, X 2¢ , Y2¢, Z2¢ — координаты век-

  

æ X i¢ö

æ x i - x0i ö

торов B, r1, r2 в системе координат объекта OXYZ; ç Y i¢ ÷ = A i ç y i - y0i ÷,

ç ÷ ç ÷

ç Z i¢ ÷ ç -f i ÷

i — номер снимка;

 

B X = X S

- X ;ü

S ï

2 1 ï

è ø è ø

B Y = Y S

- Y S ; ý

2 1

ï

(2.4.9)

B Z = Z S - Z S . ï

    2 1 þ

  Так как векторы B ´ r2 и r1 ´ r2 коллинеарны (потому, что векторы

2

B, r1, r компланарны), значение N можно найти как отношение их

модулей, то есть

 

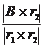N = . (2.4.10)

 

в координатной форме выражение (2.4.10) с учетом (2.4.8) имеет вид

 

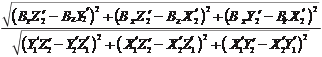N = . (2.4.11)

 

У коллинеарных векторов отношение их координат равно отноше- нию их модулей, поэтому можно записать:

N = B Y Z2¢ - B ZY2¢ ;

Y1¢Z2¢ - Y2¢Z1¢

N = B X Z2¢ - B Z X 2¢ ;

X1¢Z2¢ - X 2¢Z1¢

N = B XY2¢¢ - B Y X 2¢ . (2.4.12)

X1¢Y2¢ - X 2¢Y1¢

Таким образом, если известны элементы внутреннего и внешнего ориентирования стереопары снимков и измерены на этих снимках коор- динаты соответственных точек x1, y1 и x2, y2, то сначала надо вычислить по одной из формул (2.4.12) значение скаляра N, а затем по формуле (2.4.4) — координаты точки местности X, Y, Z.