§1.7. Формулы связи координат соответственных точек горизонтального и наклонного снимков, полученных из одного центра проекции (формулы трансформирования координат точек снимка)
 z0
z0
z
S
f о α
P0 o
x
x0
f
P
r
o
m r0
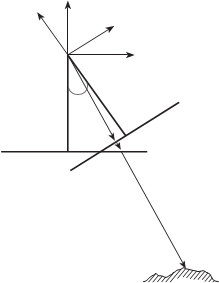
Пусть из точки S получены наклонный снимок Р съемочной камерой с фокусным расстояни- ем f и горизонтальный снимок Р0 съемочной камерой с фокусным расстоянием f о, на которых точ- ка М объекта изобразилась со- ответственно в точках m и m0 (рис. 1.16). Найдем зависимости
m0 между координатами эт и х точек.
На рис. 1.16 Sm = r и
Sm0 = r_0 — векторы, определя-
ющие положение точек m и m0 относительно центра проекции S на снимках Р и Р0. векторы
M r и r0 коллинеарны, поэтому
рис. 1.16
можно записать:
где N — скаляр.
r0 = N r, (1.7.1)
в системе координат горизонтального снимка Sx0y0z0 выражение (1.7.1) имеет вид (полагая х о = ó о = 0):
æ x0 ö æ x¢ö
ç y0 ÷ = N ç y¢÷, (1.7.2)
ç ÷ ç ÷
ç -f0 ÷
ç z¢ ÷
è ø è ø
где x′, y′, z′ — координаты вектора r в системе координат горизонталь- ного снимка,
æ x¢ö æ x - x0 ö
ç y¢÷ = Aç y - y0 ÷. (1.7.3)
ç ÷ ç ÷
ç z¢ ÷ ç -f ÷
è ø è ø
Из третьего уравнения (1.7.2) следует, что N =
-f0 .
 z¢
z¢
Подставив значение N в первые два уравнения (1.7.2), получим формулы связи координат соответственных точек горизонтального и наклонного снимков:
x0 = -f0 x¢ ; ü
z¢ ïï
(1.7.4)
0 0 y¢ ý
|
y = -f
,ï
z¢ þ
которые с учетом (1.7.3) имеют вид:
 |
x0 = -f0 a11 ( x - x0 ) + a12 (y - y0 ) - a13f ;ü
a ( x - x ) + a (y - y ) - a f ï
31 0 32 0 33 ï
(1.7.5)
a ( x - x ) + a (y - y ) - a f ý
y0 = -f0 21 0 22 0 23 .ï
|
a31 ( x - x0 ) + a32 (y - y0 ) - a33f ï
выведем формулы определения координат точек наклонного сним- ка по координатам соответственных точек горизонтального снимка. Из (1.7.1) следует, что
r = 1 r0. (1.7.6)
N
в системе координат наклонного снимка Sx yz выражение (1.7.6) имеет вид:
æ x - x0 ö æ x* ö
ç y - y ÷ = 1 ç y* ÷, (1.7.7)
ç 0 ÷ N ç ÷
ç -f ÷
ç z* ÷
è ø è ø
где х*, y*, z * — координаты вектора r0 в системе координат наклонного
снимка,
æ x* ö æ x0 ö
ç y* ÷ = AT ç y0 ÷.
(1.7.8)
ç ÷ ç ÷
ç z* ÷ ç -f0 ÷
è ø è ø
Из третьего уравнения (1.7.7) следует, что 1 =- f .

N z*
Подставляя значение 1/N в первые два уравнения (1.7.7), получим формулы связи координат точек наклонного и горизонтального снимков:
 |
x = x - f x* ;ü
o z* ïï
(1.7.9)

|
y* ý
или
y = y o - f z* ï
x = x -
a11x o + a21y o - a31f0 ;ü
 |
o f a x o + a y o - a f0 ï
13 23 33 ï
(1.7.10)
a x o + a
y o - a
f0 ý

|
y = y o - f
12
a13 x o
22
+ a23y
32
o - a33f
0 .ï








