§1.3. системы координат объекта. Элементы внешнего ориентирования съемочной камеры

Дата: 2025-06-02; Просмотры: 20

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

При решении фотограмметрических задач по снимкам положение точек объекта (местности) и съемочной камеры в момент получения снимка определяют в прямоугольной пространственной системе коорди- нат объекта OXYZ. в качестве этой системы координат при выполнении фотограмметрических работ по созданию карт и других документов о местности обычно используют геоцентрическую или топоцентрическую систему координат. Так как топографические карты и другие документы о местности создаются в государственных или местных картографиче- ских системах координат (в России в системах координат СК 42, СК 95 и Балтийской системе высот), в процессе фотограмметрической обработки

снимков её результаты преобразуют в государственные или местные системы координат и высот.

При фотограмметрической обработке снимков используют также прямоугольные системы координат, связанные с характерными точ- ками снимаемого объекта. Такие системы применяют в тех случаях, когда нет необходимости отображать объекты в государственных си- стемах координат, например, при съемке архитектурных сооружений и документации дорожных происшествий. Положение и ориентацию системы координат съёмочной камеры в системе координат объекта OXYZ определяют э л е ме н т ы в не ш не г о о р ие н т и р о в а н и я с ъ е м о ч н о й к а м е р ы. Положение центра проекции S в системе координат объекта определяют его координаты X s, Y s, Z s.

Угловая ориентация системы координат съемочной камеры от-

носительно системы координат объекта определяется ортогональной матрицей

æ a11

a12

a13 ö

æ cos Xx

cos X y

cos Xz ö

A = ç a21

a22

a23 ÷ = ç cosYx

cosY y

cosYz ÷.

(1.3.1)

ç

è a31

a32

÷

a33 ø

ç

è cos Zx

cos Z y

÷

cos Zz ø

в матрице а элементы (направляющие косинусы) а ij являются косинусами пространственных углов между осями системы координат объекта OXYZ и снимка Sx yz. Направляющие косинусы являются коор-

динатами единичных векторов (ортов), совпадающих с осями координат съемочной камеры в системе координат объекта.

вследствие особых характеристик ортогональной матрицы, како- вой является матрица направляющих косинусов

æ 1 0 0 ö

A-1 = AT ; AT A = Eç 0 1 0 ÷,

ç ÷

ç 0 0 1 ÷

è ø

поэтому в матрице направляющих косинусов независимы только три элемента, следовательно, элементы этой матрицы являются функцией трех параметров. в качестве этих параметров в фотограмметрии наи- более часто используют углы – w, a и κ, которые называют у г л о в ы - м и э л е ме н т а м и в не ш не г о о р ие н т и р о в а н и я съемочной камеры. Последовательно поворачивая систему координат объекта OXYZ вокруг ее осей на эти углы, можно ориентировать ее параллельно

осям системы координат съемочной камеры. При этом последователь- ность и направление вращений могут быть произвольными. Поэтому в фотограмметрии используют различные системы угловых элементов ориентирования съемочной камеры.

Рассмотрим наиболее широко используемую систему угловых эле- ментов ориентирования съемочной камеры, в которой система координат объекта OXYZ поворачивается последовательно против часовой стрелки (правые углы) вокруг осей X, Y и Z

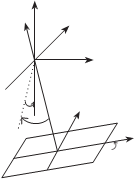соответственно на углы w, a и κ. Z

Геометрическая интерпретация z Y

угловых элементов внешнего

ориентирования показана на S X

рис. 1.10, здесь w — поперечный

угол наклона (угол в координат-

ной плоскости YZ между осью Z ω y

и проекцией оси z на плоскость α x

YZ); a — продольный угол на- клона (угол между проекцией оси z на плоскость YZ и осью z); κ — угол разворота снимка (угол в плоскости снимка Р между следом сечения этой плоскости

плоскостью Xz и осью х снимка). O

Значение элементов a ij ма-

κ

o

X

рис. 1.10

трицы а можно получить путем последовательного перемножения матриц, составленных для последовательных поворотов системы коор- динат объекта ОХYZ на углы w, a и κ. в результате поворота системы координат ОХYZ или, что то же самое, системы координат SXYZ на угол w эта система преобразуется в систему координат SX′Y′Z′ (рис. 1. 11).

в соответствии с выражением (1.3.1) матрица

æ cos 0°

cos 90°

cos 90° ö æ 1 0 0 ö

A = ç cos 90°

cosw

cos (90° + w)÷ = ç 0

cos w

-sin w÷.

w ç

ç cos 90°

cos(90° - w)

cos w

÷ ç

ø ç sin w

÷

cosw ÷

в результате поворота на угол a система координат SX′Y′Z′ преоб- разуется в систему координат SX″Y″Z″ (рис. 1.12).

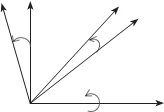Z' Z Y'

Y

ω ω

Z' Z''

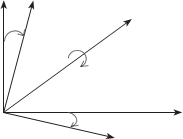α

Y'(Y'' )

α

ω S

S X(X' )

X'

α

X''

рис. 1. 11

в соответствии с выражением (1.3.1) матрица

рис. 1. 12

æ cos a

cos 90°

cos (90° - a)ö

æ cos a

0 sin a ö

A = ç cos 90°

cos 0°

cos 90°

÷ = ç 0 1 0 ÷.

a ç

ç cos (90°+ a)

cos 90°

cos a

÷ ç

÷ ç -sin a

÷

0 cosa÷

в результате поворота системы координат SX″Y″Z″ на угол κ эта система преобразуется в систему координат съемочной системы Sx yz (рис. 1.13).

в соответствии с выражением (1.3.1) матрица

æ cos k

cos(90°+ k)

cos 90°ö æ cos k

-sin k 0 ö

A = ç cos (90°- k)

cos k

cos 90°÷ = ç sin k

cos k 0 ÷.

k ç

ç cos 90°

cos 90°

÷

cos 0° ÷

ç ÷

ç 0 0 1 ÷

в результате перемножения матриц

A = AwAa Ak = Awa Ak,

получим значения элементов a ij, как функции углов w, a и κ:

a11 = cos acos k; a12 = -cosasin k; a13 = sin a;ü

a21 = sin wsin a cos k + coswsin k; ï

a = -sin wsin asin k + coswcos k; ï

22

a23 = -sin wcosa;

a31 = - cos wsin a cos k + sin wsin k; a32 = cos wsin asin k + sin wcos k; a33 = cos wcosa.

ï

ý (1.3.2)

ï

ï

ï

ï

Если известны значения направляющих косинусов a ij, то из выражений (1.3.2) можно полу- чить значения углов w, a, κ:

w = arctg æ - a23 ö;ü

Z''(z)

κ

y

Y''

κ

ç a ÷ ï

è 33 ø ï

a = arcsin (a13 ); ý (1.3.3) S κ x

æ a ö ï

X''

k = arctg ç - 12 ÷. ï

è a11 ø ïþ

рис. 1. 13

§1.4. Формулы связи координат соответственных точек снимка и местности

Пусть из точки S получен снимок Р, на котором точка М местно- сти изобразилась точкой m. Найдем зависимости между координатами

этих точек. Положение точки М местности в си_стеме координат объекта

OXYZ определяет вектор R M

OM .

вектор R S

= OS

определяет поло-

жение цент ра п р оекции S в системе координат объекта OXYZ. векторы

r_ = Sm и R = SM определяют соответственно положение точек m и М

относительно центра проекции S. Из рис. 1.14 следует, что

  

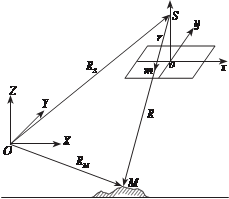R M = R S + R. (1.4.1) z



векторы R и r коллине-

арные, поэтому можно записать:



R = N r , (1.4.2)

где N — скалярная величина.

С учетом (1.4.2) выражение (1.4.1) имеет вид

  

R M = R S + N r. (1.4.3)

в координатной форме вы- ражение (1.4.3) имеет вид

рис. 1. 14

æ X ö æ X S ö æ X ¢ö

ç Y ÷ = ç Y S ÷ + N ç Y ¢ ÷

ç ÷ ç ÷ ç ÷

ç Z ÷ ç Z S ÷ ç Z ¢ ÷

или

è ø è ø è ø

X = X S + NX ¢;ü

ï

Y = Y S + NY ¢;

(1.4.4)

Z = Z S + NZ ¢. ï

в выражении (1.4.4) X, Y, Z — координаты точки М в системе ко- ординат объекта; X S, Y S, Z S — координаты центра проекции S в системе координат объекта; X′, Y′, Z′ — координаты вектора r в системе коор- динат объекта. Очевидно, что

æ X ¢ö æ x - x0 ö

ç Y ¢ ÷ = A ç y - y0 ÷, (1.4.5)

ç ÷ ç ÷

ç Z ¢ ÷ ç -f ÷

è ø è ø

где а — матрица преобразования координат, элементы a ij которой опре- деляются по значениям угловых элементов внешнего ориентирования снимка w, a, κ.

Из третьей формулы выражения (1.4.4) следует, что

N = Z - Z S .

Z ¢

Подставив значение N в первые две формулы выражения (1.4.4), получим формулы связи координат соответственных точек местности и снимка

X = X

+ (Z - Z

) X ¢ ;ü

S S Z ¢ ïï

Y ¢ ý

(1.4.6)

Y = Y S + (Z - Z S ) Z ¢ , ï

которые с учетом (1.4.5) имеют вид:

X = X

+ (Z - Z

) a11(x - x0 ) + a12 (y - y0 ) - a13f ;ü

S S a

(x - x ) + a

(y - y ) - a

f ïï

Y = Y

+ (Z - Z

31 0 32 0 33 ý

) a21(x - x0 ) + a22 (y - y0 ) - a23f . ï

(1.4.7)

S S a (x - x ) + a (y - y ) - a f ï

31 0 32 0

33 þ

Из формул (1.4.6) следует, что координаты точки местности можно получить по координатам ее изображения на снимке, если известны элементы внутреннего и внешнего ориентирования снимка и высота Z этой точки. Найдем формулы связи координат соответственных точек снимка и местности, которые позволят вычислить координаты изобра- жения точки на снимке в системе координат снимка по координатам соответственной точки местности, определенным в системе координат объекта OXYZ.

Из выражения (1.4.3) следует, что

r = 1 ( 

 ). (1.4.8)

в координатной форме выражение (1.4.8) имеет вид

æ x - x o ö æ x* ö

ç y - y

÷ = 1 ç y* ÷

ç o ÷ N ç ÷

ç -f ÷ ç z* ÷

или

è ø è ø

x = x

+ 1 x*; ü

0

y = y0

N

+ 1

N

ï

ï

y*; ï

ï

(1.4.9)

-f = 1 z*. 

N þ  

в выражении (1.4.9) x*, y*, z* — координаты вектора стеме координат снимка Sx yz.

R M - R S

в си-

æ x* ö æ X - X S ö

ç y* ÷ = AT ç Y - Y ÷.

(1.4.10)

ç ÷ ç S ÷

ç z* ÷

ç Z - Z S ÷

è ø è ø

Из третьего выражения (1.4.9) следует, что

1 =- f .

Подставив значение 1

N

N z*

в первые два уравнения выражения (1.4.9),

получим формулы связи координат соответственных точек снимка и местности:

x = x - f x* ; ü

0 z* ïï

y* ý

(1.4.11)

y = y0 - f

которые с учетом (1.4.10) имеют вид

z* ,ï

x = x

- f a11( X - X S ) + a21(Y - Y S ) + a31(Z - Z S ) ;ü

0 a ( X - X ) + a

(Y - Y ) + a

(Z - Z

) ïï

13 S 23

S 33

S ý (1.4.12)

y = y

- f a12 ( X - X S ) + a22 (Y - Y S ) + a32 (Z - Z S ) .ï

0 a ( X - X ) + a

(Y - Y ) + a (Z - Z ) ï

13 S 23

S 33 S þ

Формулы (1.4.12) в фотограмметрии часто называют у р а в н е н и -

ями к о л лин е а р н о с т и.