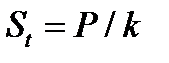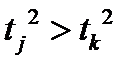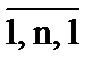Значения элементов 1 -1 -1 3
Квадрат значения 1 1 1 9
Упорядоченные элементы 3 -1 -1 1
Всего четыре числа подошло к необходимым нам условиям. В этом случае, массив будет упорядочен. Кроме этого, может возникнуть проблема, что таких чисел вообще не будет. В этом случае массив останется неизмененным.
Алгоритм решения задачи.
При разработке алгоритме будем использовать метод декомпозиции: решение задачи сначала опишем в виде основного алгоритма, использующего вспомогательные алгоритмы решения задач частей задания. Затем опишем вспомогательные алгоритмы – модули решения задач каждой части. При разработке и описании алгоритмов используются элементарные структуры алгоритмов, составляющие основу структурного программирования.
Основной алгоритм.
При разработке основного алгоритма нужно учесть обязательные требования, сформулированные в постановке задачи и рекомендации по разработке сложных программ:
1. Необходимо задачу решать в общем виде, для любых допустимых значений исходных данных.
2. Предусмотреть возможность выполнения 3 вариантов расчёта.
Введём вспомогательную переменную Vt для управления вариантом расчёта: если Vt=0 – тестовый расчёт, Vt=1 – без Randomize, любое другое значение Vt – расчёт с Randomize.
3. Модули должны быть относительно независимы: обязательно иметь имя, свои входные, выходные и промежуточные данные, не использовать глобальные переменные.
4. Действия алгоритма поясняются на естественном языке, в обозначениях постановки задачи, не используются конструкции языка программирования.
3.1 Основной алгоритм.
| Данные теста:
12, -1, 3, t(1:12)
|
| Vt, n, i, a, b: integer t: vector St: real //Vt – вводимое число
//a – вводимое число
//b – вводимое число
|
| Вычисление сред. ариф. St
|
| Определение максимального
элемента
|
| //t – массив (исх. и изм.)
// St – искомая функция
// M - искомая функция
|
3.2 Алгоритм получения элементов вектора.
| i:integer
//Vt – вариант расчёта
//n – количество элементов
//a – нижняя граница
//b – верхняя граница
|
| ti=a+round((b–a)·
·random(100)/100)
|
| //t(1:n) – искомый вектор
|
3.3 Алгоритм вычисления среднеарифметического значения нечетных по номеру элементов третьей четверти массива.
| i,k,P:integer //P – известное число //k – известное число
//n – известное число //St - известное число //t(1:n) – известный вектор
|
3.4 Алгоритм определения максимального значения среди отрицательных элементов второй половины массива.
| i,k,M:integer
//M – известное число //k – известное число //t(1:n) – известный вектор
|
| Вывод «Нет нужных элементов»
|
| //M – искомая функция //i – номер функции //ti – значение функции
|
3.5 Упорядочение каждых третьих элементов всего массива по убыванию квадратов значений.
| i,j,k,buf:integer
//t(1:n) – известный вектор //k – промежуточная переменная
|
| //t(1:n) – искомый вектор
|
4. Таблицы переменных задачи
Таблица переменных основного алгоритма
|
Смысл переменных
| Обозначение
| Тип переменной
| Примечания
| |
| в алгоритме
| в программе
| |
| Исходные данные:
| |
| Вариант расчёта
| Vt
| Vt
| Целый
| VtÎZ
| |
| Размер массива
| n
| n
| Целый
| 1< n <100
| |
| Наименьшее значение элемента
| a
| a
| Целый
| a Î[-32761; 32767]
a <=b
| |
| Наибольшее значение элемента
| b
| b
| Целый
| b Î[-32761; 32767]
a <=b
| |
| Промежуточные данные:
|
i
|
i
|
Целый
| i= 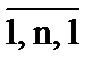
| |
| Номер элемента массива
| |
| Результаты:
|
St
|
St
|
Веществ.
| StÎR
| |
| Среднеарифметическое значение
| |
| Вектор
| t
| t
| Одномерный массив
|
| |
Таблица переменных алгоритма получения вектора ( Part _1)
| Смысл переменных
| Обозначение
| Тип переменной
| Примечания
| |
| в алгоритме
| в программе
| |
| Входные данные:
| |
| Вариант расчёта
| Vt
| Vt
| Целый
| VtÎZ
| |
| Размер массива
| n
| n
| Целый
| 1< n <100
| |
| Наименьшее значение элемента
| a
| a
| Целый
| a Î[-32761; 32767], a <=b
| |
| Наибольшее значение элемента
| b
| b
| Целый
| b Î[-32761; 32767], a <=b
| |
| Промежуточные данные:
|
i
|
i
|
Целый
|
i= 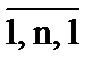
| |
| Номер элемента массива
| |
| Выходные данные:
| t
| t
| Одномерный массив
|
tiÎ[a;b]
| |
| Массив
| |