Исходными данными являются значения количества элементов в массиве n и отрезок [a, b].

Дата: 2025-06-14; Просмотры: 1
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Порядок решения задачи: сначала нужно получить одномерный массив (часть 1), затем можно вычислить параметр массива (часть 2) или найти нужный элемент (часть 3). Упорядочение массива (часть 4) нужно выполнить в последнюю очередь, так как перестановка элементов массива при упорядочении может повлиять на вычисление параметра массива и определение нужного элемента.

Для лучшего понимания задачи, выявления её особенностей выполним тестовый расчёт.

Возьмём любые исходные данные, например n=12, а =-1, b = 3. Запишем 12 случайных целых чисел от -1 до 3 – это значения элементов массива T для тестового расчёта.

 

0, 2, 1, 0, 1, -1, 3, 0, -1, 0, 1, 3

Часть 2.

Для вычисления среднеарифметического значения сначала нужно выделить в общем виде номера элементов третьей четверти массива. Номер первого найдем по формуле: n/2 + 1=12/2+1=7. Номер последнего найдем по формуле: 3*12/4=9.

Запишем элементы третьей четверти массива

 

x 7 x8 x 9

3 0 -1

 

Выделим подчёркиванием нужные элементы: нечетные по номеру.

Нужных элементов к = 2. Среднеарифметическое значение
St = .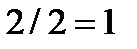

При вычислении St может возникнуть следующая проблема:

  1. Не будет нужных элементов (к = 0), например, если все элементы третьей четверти равны 0. В этом случае выведем : «Для среднего арифметического нет нужных элементов».

Выявленные возможные проблемы нужно учесть при разработке алгоритма.

 

Часть 3.

Для определения максимального значения сначала выделим элементы второй половины массива: номер первого элемента: 12/2 + 1=7, номер последнего будет соответствовать номеру последнего элемента массива.

Запишем элементы второй половины массивы:

 

x7 x8 x 9 x10 x11 x12

3 0 -1 0 1 3

Выделим подчёркиванием нужные элементы: отрицательные. Нужных элементов 1, максимальное значение равно -1, такое значение имеет один элемент: x9 = -1.

 

 

При решении данной задачи могут быть следующие ситуации:

1. Не будет нужных элементов;
2. Будет единственный элемент с максимальным значением;
3. Будет множество элементов с максимальным значением.

Часть 4.

При выборочном упорядочивании каждых третьих элементов сначала нужно выделить необходимую часть массива, в нашем случае это весь массив.

Запишем каждые третьи элементы всего массива:

Элементы x3 x6 x9 x12