§1.1. основные свойства кадрового снимка
а.П. Михайлов а.Г. Чибуничев
фотограмметрия
Под общей редакцией
доктора технических наук, профессора а.Г. Чибуничева
Москва Издательство МИИГаик
2016
Удк 528.7
ББк 26.12
М 69
рецензенты:
ФГБУ «Федеральный научно-технический центр геодезии, картографии и инфраструктуры пространственных данных»
(кандидат техн. наук С.а. Кадничанский); доцент, кандидат техн. наук В.м. Курков (МИИГаик)
м 69
михайлов а.П., Чибуничев а.г.
Фотограмметрия: Учебник для вузов / Под общ. ред. а.Г. Чибуничева.
–М.: Изд-во МИИГаик, 2016. – 294 с.: ил.
ISBN 978-5-91188-070-5
Изложены теория одиночного и пары снимков, фототриангуляция. Рас- смотрены вопросы автоматизации фотограмметрических измерений, выполняе- мых по цифровым изображениям, создания цифровых ортофотопланов, вопросы наземной фотограмметрии и лазерного сканирования, фотограмметрические методы обработки изображений, полученных системами дистанционного зон- дирования, а также стереофотограмметрические системы.
для студентов геодезических вузов и инженерно-технических работников аэрогеодезического производства.
Удк 528.7
ББк 26.12
ISBN 978-5-91188-070-5
© Михайлов а.П., Чибуничев а.Г., 2016
|
© Издательство МИИГаик, 2016
ВВеДеНие
Фотограмметрия — научно-техническая дисциплина, занимаю- щаяся определением геометрических характеристик объектов (форма, размеры, положение в пространстве и т.д.) по их изображениям. термин
«фотограмметрия» происходит от трех греческих слов: photos — свет, gramma — запись, metrio — измерение и дословно переводится, как измерение по светозаписи или в современной интерпретации — из- мерение по фотоснимку.
в настоящее время в фотограмметрии применяются не только аналоговые и цифровые фотоснимки, но и изображения, получаемые с помощью радиолокационных, лазерно-локационных, рентгеновских и других съемочных систем. Наибольшее применение фотограмметрия находит в области картографии для создания карт различного назначе- ния, а также других документов о местности по аэро-, космическим и наземным снимкам, получаемым различными съемочными системами. Помимо картографирования земли фотограмметрия применяется для создания карт и изучения поверхности планет, их спутников и других небесных тел. очень широко фотограмметрические методы исполь- зуются для решения различных задач в архитектуре и строительстве, промышленности, криминалистике, медицине и других областях чело- веческой деятельности, что обусловлено высокой точностью и произво- дительностью фотограмметрических методов, а также возможностью изучения статических и динамических объектов и процессов.
Фотограмметрия как наука появилась в середине XIX столетия вскоре после изобретения фотографии. однако использование пер- спективных изображений при составлении топографических карт было осуществлено значительно раньше. теоретическое обоснование возможности определения формы, размеров и положения объекта в пространстве по его перспективному изображению было дано в 1759 г. И.о. ламбертом в работе «свободная перспектива». в 1764 г. великий
3
русский ученый М.в. ломоносов в инструкции для географических исследований России предложил составлять перспективные рисунки местности с помощью камеры-обскуры. в 1839 г. французский ученый Ж.М. дагер применил для фиксации изображения, получаемого с по- мощью такой камеры, светочувствительное серебро, которое наносилось на металлическую пластинку. На этой пластинке получалось позитивное фотографическое изображение. так появилась фотография.
Применять фотографии для создания топографических карт впер- вые предложил французский геодезист доминик Ф. араго примерно в 1840 г., а в 1860 г. французский военный инженер Э. лосседа выполнил фотографирование Парижа с крыши высокого здания и по фотосним- кам создал план, точность которого оказалась выше плана, получен- ного геодезическим методом. Этой работой было положено начало фотограмметрического метода съемки, который в последующие годы совершенствовался и стал применяться во многих странах. в России первые фототопографические съемки были выполнены в 1891–1898 гг. инженерами Н.о. виллером, Р.Ю. тиле, П.И. Щуровым для целей трас- сирования железных дорог в закавказье и восточной сибири.
в истории развития фотограмметрии выделяют три основных пе- риода, которые можно условно назвать — аналоговая, аналитическая и цифровая фотограмметрия.
а н а л о г о в а я ф о т о г р а м м е т р и я берет свое начало с изо- бретения в 1901 г. к. Пульфрихом стереокомпаратора. Этот прибор позволяет измерять координаты точек снимков, составляющих стерео- пару. далее развитие фотограмметрии пошло по пути создания специ- альных опти-ческих и механических приборов, предназначенных для непосредственного создания карт по аэро- и наземным снимкам. Эти приборы позволяют выполнить все процессы преобразования снимков в карту. Первый такой прибор, стереоавтограф, был разработан в 1909 г. (е. орель) для создания карт по наземным снимкам. в 1915 г. Газзер запотентовал стереопроектор, который стал прототипом мультиплек- са, позволяющего построить стереоскопическую модель на экране по множеству снимков и измерять ее с целью создания карты. в 1932 г. Ф.в. дробышев изобрел стереометр, позволяющий рисовать рельеф местности непосредственно на снимках. контурную часть карты полу- чали по фотопланам, составленных по множеству трансформированных снимков. трансформирование снимков выполняли на специальных
4
|
приборах, называемых фототрансформаторами, которые позволяют преобразовать наклонный снимок в горизонтальный. в этот период в России и за рубежом было разработано достаточно много различных универсальных фотограмметрических приборов, которые используются на некоторых предприятиях и в настоящее время.
а н а л и т и ч е с к а я ф о т о г р а м м е т р и я. Этот этап в развитии фотограмметрии начинается с появлением ЭвМ (примерно в 1950 г.). Начиная с этого времени стали развиваться аналитические методы фотограммет-рической обработки снимков, которые продолжают со- вершенствоваться и в настоящее время. в 1957 г. У.в. Хелава (канада) разработал первый аналитический универсальный прибор, представля- ющий собой сочетание стерекомпаратора и электронной вычислитель- ной машины. На стереокомпараторе выполнялись измерения координат точек снимков, а на ЭвМ — все преобразования этих измерений в про- екцию карты. По сравнению с аналоговыми аналитические приборы позволяют значительно повысить точность обработки снимков и произ- водительность. таких приборов и систем было разработано достаточно много (Швейцария, Германия, Франция, Италия, Россия и Украина). в настоящее время они не выпускаются, но используются на производстве. Ц и ф р о в а я ф о т о г р а м м е т р и я начала развиваться с появ- лением цифровых изображений. в начале 90-х годов прошлого столе- тия появились первые коммерческие цифровые фотограмметрические системы, позволяющие решать все фотограмметрические задачи на компьютере, включая стереоскопическое наблюдение и измерение снимков на экране компьютера. отличительной особенностью циф- ровых фотограмметрических систем является возможность широкой автоматизации всех процессов преобразования снимков в карту. Это направление в развитии фотограмметрии в настоящее время является
основным и широко применяется на производстве.
 |
|
Глава 1
 |
Теория одиночного кадрового снимка
§1.1. основные свойства кадрового снимка
Из курса аэрокосмических съемок известно, что для получения аэрокосмических снимков земной поверхности и расположенных на ней объектов используют кадровые и сканерные съемочные системы. в кадровых съемочных системах снимок формируется объективом одномоментно для всех точек снимка на расположенной в фокальной плоскости объектива светоприемной матрице (или фотоматериале). в съемочных камерах, предназначенных для получения кадровых сним- ков, используются центральные или электронные затворы.
Кадровый снимок представляет собой центральную проекцию снимаемого объекта на плоскость если на снимке отсутствуют сме- щения точек, вызываемые дисторсией объектива съемочной камеры, атмосферной рефракцией и другими причинами (рис. 1.1). Совокупность проектирующих лучей, при по-
мощи которых получен снимок, называют связкой проектирую- щих лучей, а точку, в которой пересекаются проектирующие лучи — центром проекции S.
При центральном проекти- ровании различают негативное (обратное) и позитивное (прямое) изображения (рис. 1. 2).
Позитив P получают в слу- чае, когда объект и плоскость проекции расположены по одну
рис. 1.1
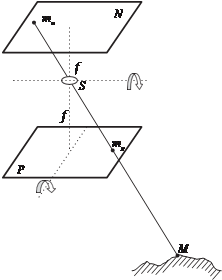рис. 1.2
сторону от центра проекции S, а негатив N — в в случае когда объект и плоскость проекции расположены по разные стороны от центра проекции S. Негатив и позитив располагаются сим- метрично по разные стороны от центра проекции S. Если не- гатив развернуть на 180° вокруг оси, проходящей через центр проекции S параллельно пло- скостям негатива и позитива, а затем развернуть вокруг оси, лежащей в плоскости позитива и перпендикулярной к оси первого разворота, то все точки негатива совпадут с точками позитива. Поэтому при анализе снимка можно рассматривать как нега-
тив, так и позитив. в дальнейшем чаще будем рассматривать позитив, который, как и негатив, будем называть снимком.
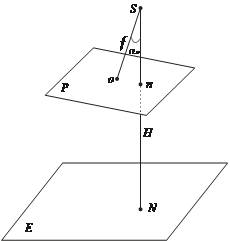Рассмот рим некоторые элементы центральной про- екции. На рис. 1.3: P — пло- скость снимка; E — пред- метная (горизонтальная) пло- скость; S — центр проекции (точка фотографирования); о — главная точка снимка — след пересечения плоскости снимка главным лучом (главный луч — это луч, проходящий через центр проекции S перпен- дикулярно к плоскости снимка);
S = f — фокусное расстояние
рис. 1.3
о
съемочной камеры — рассто- яние от центра проекции S до
главной точки снимка; n — точ- S
ка надира — пересечение от- весной линии, проходящей через центр проекции, с плоскостью снимка; N — проекция точки надира снимка на плоскость Е; SN = H — высота фотографирова- ния (высота центра проекции от- носительно предметной плоско-
сти); α0 — угол наклона снимка.
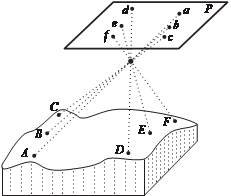
Из рис. 1.3 следует, что on = f tgα0. любая точка местности М
на снимке изображается точ- кой m (рис. 1.4). Прямой линии на местности (K–L) в общем случае соответствует прямая (k–l) на снимке. в частном случае, когда
рис. 1. 4
прямая линия на местности (D–F) проходит через центр проекции S, она изображается на снимке в виде точки (d f). Точка надира n является точкой схода изображений на снимке вертикальных линий объекта (рис. 1.5).
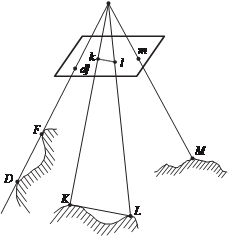
На рис. 1.5 AB и DM — вертикальные линии на объекте, а ab и dm — их изображения в плоскости снимка P. Если продолжить изо- бражения вертикальных линий ab и dm, то они пересекутся в точке на- дира n. Для доказательства этого достаточно провести плоскости через вертикальные линии AB и DM и
центр проекции S. Так как эти плоскости вертикальные, то они пересекутся по вертикальной ли- нии SN, проходящей через центр проекции S и точку надира n (ко- торая по определению является точкой пересечения плоскости снимка с отвесной линией, опу- щенной из центра проекции S). Очевидно, что изображения ab и dm вертикальных линий AB и
S
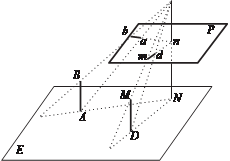рис. 1. 5
рис. 1.6
T
рис. 1.7
рис. 1.8
DM находятся на следах сечения плоскости снимка вертикальны- ми плоскостями SAB и SDM и пересекаются в точке надира n.
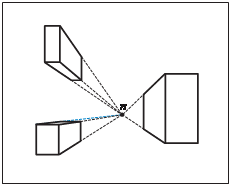На рис. 1.6 приведен пример изображения на снимке зданий прямоугольной формы.
линия действительного горизонта ii является геометри- ческим местом точек схода i изо- бражений параллельных прямых линий, расположенных в пред- метной плоскости E (рис. 1.7).
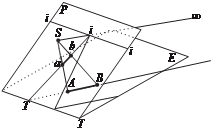Построим изображение пря- мой АВ, расположенной в пред- метной плоскости Е (см. рис 1.7).
∞ Для этого сначала продолжим
данную прямую до пересечения с линией основания ТТ (линия пересечения плоскости снимка с предметной плоскостью). Полу- ченная таким образом точка Т является одновременно и изобра- жением на снимке. Теперь про- должим линию АВ в обратном направлении до бесконечности. Очевидно, что проектирующий луч, идущий от бесконечно уда- ленной точки, принадлежащей прямой линии, параллелен этой линии и пересекает снимок в точке схода i, лежащей на линии действительного горизонта. Изо- бражение линии на снимке полу- чают в результате соединения точек i и Т.
аналогично строят изобра-
жения других линий. Если они параллельны между собой в плоскости Е, то их изображения на снимке пересекаются в точке схода i. На рис. 1.8 приведен пример изображения на перспективном снимке прямых участ- ков дороги и прямоугольного объекта.