Решение задач запиши в тетрадь
№ 1201.
Нет.
№ 1202.
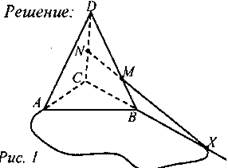
Решение:
Прямая MN принадлежит плоскости BCD, которая пересекается с плоскостью АВС по ВС. Продолжим ВС до пересечения с прямой MN в точке X. Точка Х принадлежит и прямой MN, и плоскости АВС, так как точка X лежит на прямой ВС, принадлежащей плоскости АВС.
№ 1203.
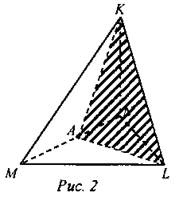
Решение:
По условию МА = NA. Проводим отрезок AL, так как точки L и A принадлежат одной плоскости MNL. Проводим отрезок АК, так как точки К и А принадлежат одной плоскости MKN. Искомое сечение - треугольник AKL.
№ 1204.
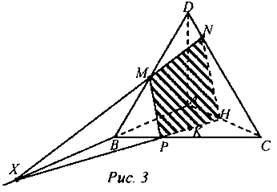
Решение:
1) Проводим прямую MN, продолжаем АВ до пересечения с прямой MN в точке X.
2) Точка X принадлежит плоскости АВС, и точка К принадлежит плоскости АВС, тогда проводим прямую ХК, пересекающую прямые ВС и АС в точках Р и Н соответственно.
3) Проводим отрезки МР, NH и PH. Четырехугольник PMNH - искомое сечение.
№ 1206.
Решение:
Найдем сумму площадей боковых граней правильной пирамиды. Так как гранями боковыми правильной пирамиды являются равные равнобедренные треугольники и площадь треугольника равна, то сумма площадей всех треугольников равна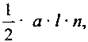 
где а - сторона основания правильной пирамиды, n - количество сторон основания, l - апофема.
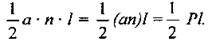
Значит, площадь боковой поверхности правильной пирамиды равна: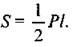 
№ 1241.
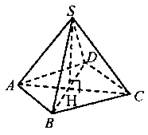
Решение:
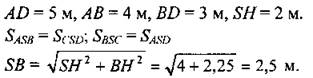
В ∆ABD: AD2 = AB2 + BD2, следовательно, он прямоугольный с прямым углом ABD.
Из ∆АВН по теореме Пифагора:
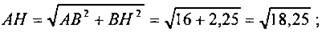
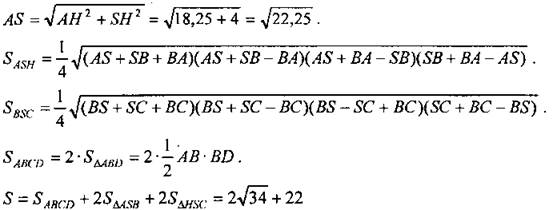
5. Итоги урока.
6. Домашняя работа:
изучить материал пункта 128; повторить пункты 122-127; ответить на вопросы 1-14 в учебнике на с. 327; решить задачи № 1202 (б), 1211 (а), 1207