Высота пирамиды - это перпендикуляр, опущенный из вершины на основание пирамиды.
31.03.2023
Тема урока: Пирамида. Правильная пирамида. Площадь поверхности.
Тип урока: объяснение нового материала
Цель урока: дать определение пирамиды, основные виды пирамиды; рассмотреть элементы пирамиды: основание, боковые грани, вершина, боковые рёбра, высота пирамиды, высота боковой грани; формирование умений учащихся в решении тематических задач.
Ход урока
1. Организационный момент.
2. Актуализация опорный знаний.
Что называется призмой? прямой призмой? правильной призмой?
- Объясните, что такое параллелепипед? Дайте определение прямого параллелепипеда, прямоугольного параллелепипеда.
- Сформулируйте свойство четырех диагоналей параллелепипеда.
- Сформулируйте основные свойства объемов.
- Что такое измерения прямоугольного параллелепипеда?
- Сформулируйте свойство диагонали прямоугольного параллелепипеда.
- Чему равен объем куба? Объем прямоугольного параллелепипеда?
- Какой формулой выражается объем призмы?
3. Изучение нового материала.
Пирамида — это многогранная объемная фигура, ограниченная плоским многоугольником (основой) и треугольниками, имеющих общую вершину, не лежащую в плоскости основания.
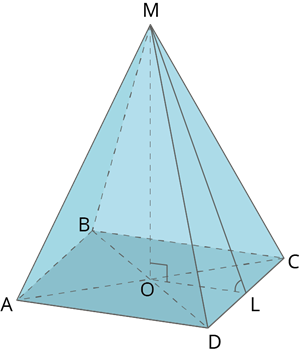Боковая грань - это треугольник, у которого один угол лежит в вершине пирамиды, а противоположная ему сторона совпадает со стороной основания (многоугольника).
Боковые ребра - это общие стороны боковых граней. У пирамиды столько ребер сколько углов у многоугольника.
Высота пирамиды - это перпендикуляр, опущенный из вершины на основание пирамиды.
Апофема - это перпендикуляр боковой грани пирамиды, опущенный из вершины пирамиды к стороне основания.
Диагональное сечение - это сечение пирамиды плоскостью, проходящей через вершину пирамиды и диагональ основания.
Правильная пирамида - это пирамида, в которой основой является правильный многоугольник, а высота опускается в центр основания.
Боковая поверхность пирамиды - это совокупная площадь всех боковых граней пирамиды.
Полная поверхность пирамиды - это совокупность площадей боковой поверхности и площади основания пирамиды.
Площадь боковой поверхности правильной пирамиды через периметр основания и апофему:
| Sb = | 1 | ph |
| 2 |
Свойства пирамиды:
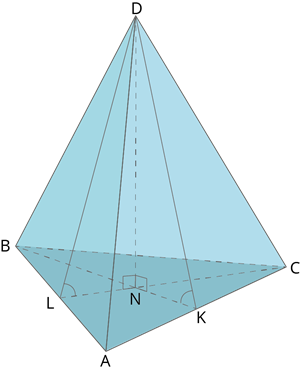Если все боковые ребра равны, то вокруг основания пирамиды можно описать окружность, а центр основания совпадает с центром окружности. Также перпендикуляр, опущенный из вершины, проходит через центр основания (круга).
Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами.
Боковые ребра равны тогда, когда они образуют с плоскостью основания равные углы или если вокруг основания пирамиды можно описать окружность.
Если боковые грани наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проектируется в ее центр.
Если боковые грани наклонены к плоскости основания под одним углом, то апофемы боковых граней равны.
Свойства правильной пирамиды:
1. Вершина пирамиды равноудалена от всех углов основания.
2. Все боковые ребра равны.
3. Все боковые ребра наклонены под одинаковыми углами к основанию.
4. Апофемы всех боковых граней равны.
5. Площади всех боковых граней равны.
6. Все грани имеют одинаковые двугранные (плоские) углы.
7. Вокруг пирамиды можно описать сферу. Центром описанной сферы будет точка пересечения перпендикуляров, которые проходят через середину ребер.
8. В пирамиду можно вписать сферу. Центром вписанной сферы будет точка пересечения биссектрис, исходящие из угла между ребром и основанием.
9. Если центр вписанной сферы совпадает с центром описанной сферы, то сумма плоских углов при вершине равна π или наоборот, один угол равен π/n, где n - это количество углов в основании пирамиды.
4. Закрепление. Решение задач.