Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются окружности.
31.01.2023 Геометрия9
Тема урока: «Формулы радиусов вписанных и описанных окружностей правильных многоугольников"
Цели урока: выработать у учащихся умение использовать формулы, связывающие радиус описанной окружности и радиус вписанной окружности со стороной а правильного n-угольника, на их основе научить учащихся получать формулы для вычисления аn через R и r и конкретизировать их для случая n = 3, n = 4, n = 6, выработать навыки применения полученных знаний при решении задач.
Тип урока: Урок закрепления знаний и умений.
Ход урок
1. Организационный момент
2. Актуализация опорных знаний. Проверка д/з.
Фронтальный опрос:
· Какая фигура называется многоугольником?
· Какой многоугольник называется правильным?
· Какое другое название правильного треугольника?
· Какое другое название правильного четырехугольника?
· Формула суммы углов выпуклого многоугольника.
· Формула угла правильного многоугольника.
3. Повторение изученного материала .
Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются окружности.
Окружность называется описанной около многоугольника, если все вершины многоугольника лежат на окружности.
Окружность можно вписать или описать около любого треугольника, причём центр вписанной в треугольник окружности лежит на пересечении биссектрис треугольника, а центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров.
Около любого правильного многоугольника можно описать окружность, и в любой правильный многоугольник можно вписать окружность, причём центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.
Формулы для радиусов вписанных и описанных окружностей правильного треугольника, правильного четырехугольника, правильного шестиугольника.
Радиус вписанной окружности в правильный многоугольник (r):
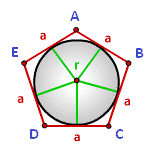 a - сторона многоугольника
a - сторона многоугольника 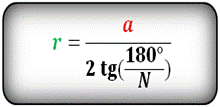
N - количество сторон многоугольника
Радиус описанной окружности правильного многоугольника( R):

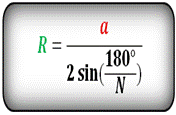
a - сторона многоугольника
N - количество сторон многоугольника.
Запомни таблицу для правильного треугольника, правильного четырехугольника, правильного шестиугольника.
| n | а | R | r | S | S | |
| 3 | 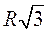
| 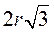
| 2r | 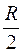
| 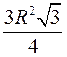
| 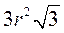
|
| 4 | 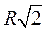
| 2r | 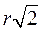
| 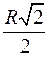
| 2R2 | 4r2 |
| 6 | R | 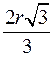
| 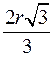
| 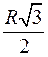
| 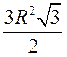
| 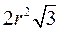
|
| n |
| 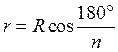
| 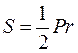
| |||
4. Решение задач
1. Решение учащимися задач на непосредственное применение выведенных формул:
1) В окружность радиуса R = 12 вписан правильный n-угольник. Определите его сторону и периметр, если: а) n = 3; б) n = 4; в) n = 6.
2) Около окружности радиуса r = 6 описан правильный n-угольник. Определите его сторону и периметр, если: а) n = 3; б) n = 4; в) n = 6.
3) Для правильного n-угольника со стороной а = 6 см найдите радиус описанной около него окружности, если: а) n = 3; б) n = 4; в)n = 6.
2. Решить задачу № 1089.
Решение
РD = 18 см; а = 18 : 3 = 6 (см);
а3 = R 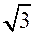 ;
;  R =
R = 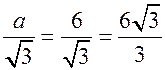 = 2
= 2 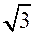 (см);
(см);
а4 = R 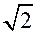 = 2
= 2 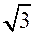 ∙
∙ 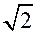 = 2
= 2 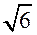 (см).
(см).
Ответ: 2 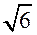 см.
см.
3. Решить задачу № 1090.
Решение
а3 = 3 см;
R = 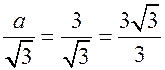
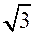 (см);
(см);
d = 2R = 2 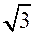 (см).
(см).
ответ: 2 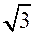 см.
см.
4. Решить задачу № 1092.
Решение
Р = 48 см;
а6 = 48 : 6 = 8 (см);
а6 = 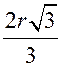 = 8 (см);
= 8 (см);
r = 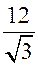 = 4
= 4 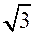 (см);
(см);
а4 = 2r = 8 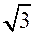 (см) ;
(см) ;
Р = 4 ∙ а4 = 8 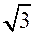 ∙ 4 = 32
∙ 4 = 32 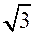 (см).
(см).
Ответ: 32 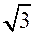 см.
см.
5.Задание на дом
Изучить материал пункта 109-113; решить задачи №№ 1087, 1088
6. Итог урока