3. Поняття простих відсотків та капітал

Дата: 2025-06-14; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

4. Геометрична прогресія та складні відсотки

5. Властивості геометричної прогресії

6. Поняття складних відсотків та капітал

Л Е К Ц І Я 36

Тема: Математика фінансів

Мета: сформувати поняття рахунків накопичення, розрахунків ренти, погашення боргу; застосування понять до розв’язування економічних задач.

Література: [2, с. 380-391]; [4, с. 255-263].

П Л А Н

1. Рахунки накопичення

2. Розрахунки ренти

3. Погашення боргу

Основні проблеми математики фінансів — обчислення про­стих та складних відсотків прибутку, розглянуто у розділах 3.2 та 3.3. Зараз ознайомимось з деякими іншими важливими зада­чами фінансової сфери.

1. Рахунки накопичення

Найпростішим типовим рахунком накопичення є такий раху­нок фізичної або юридичної особи, на який регулярно начисляється і зараховується (наприклад, в кінці кожного місяця або на початку

наступного року) фіксований доход та робиться ба­ланс вкладень і запланованих відсотків з врахуванням терміну одержаних вкладень.

Приклад 1. Кожного місяця робітник вносить 100 гривень на свій рахунок накопичення з одержанням прибутку величиною 1/2% за кожен місяць. Обчислити величину його накопичень: а) - безпосередньо після здійснення 25 внеску; б) безпосередньо після здійснення n внеску.

Розв'язування. а) Кожен внесок за місяць зростає в 1,005 рази (0,5% за місяць). Тому перший внесок за 24 місяця перебування ра­хунку прийме значення 100 • (1,005)²⁴. Другий внесок знаходився на рахунку 23 місяця, тому він прийме значення 100 • (1,005)²², третій вне­сок стане 100 ● (1,005)²², і т.д. Отже, загальна сума накопиченого рахун­ку робітника прийме значення

S = 100 • (1,005)²⁴ + 100(1,005)²³ + ... + 100 • (1,005) + 100.

Якщо розглядати праву частину в оберненому порядку, тоді її мож­на розглядати як геометричну прогресію з першим членом b1=100 і знаменником q= 1,005. Тому, використовуючи формулу суми скінченної геометричної прогресії, одержимо

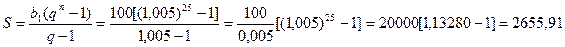
Таким чином, після 24 місяців робітник буде мати на своєму рахун­ку накопичення 2 655,9 гривень.

б) Для знаходження величини рахунку

накопичення безпосередньо після здійснення n внеску, слід рахувати (n-1) місяць першого вкладу. Після (n-1) місяця перший вклад величиною 100 гривень зросте до 100- (1,005)^n-1, другий вклад зросте до 100- (1,005)^n-2 і т.д. Таким чи­ном, загальним значенням рахунку накопичення буде сума

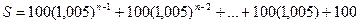
Знову одержали суму геометричної прогресії з першим членом 100 (розглядаємо її в оберненому порядку) і знаменником q= 1,005. Тому вона буде мати вигляд

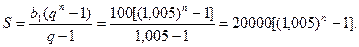(1)

Зауваження. Формула (1) дозволяє знайти величину накопичених коштів при умовах задачі за довільну кількість місяців. Наприклад, після 59 місяців на рахунку буде

20000[(1,005)⁵⁹-1] = 20000[1,34885-1]=6977 гривень

Тепер узагальнимо проведені при розв'язанні прикладу 1 міркуван­ня на випадок, коли перший внесок на рахунок накопичення дорівнює величині Р, а постійний відсоток зростання величини коштів дорівнює К за кожен певний період. У фінансових розрахунках засто­совують позначення

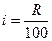(2)

При таких позначеннях величина накопичених коштів на рахунку після (n - 1) періоду їх зберігання

буде

S=P(1+i)^n-1+P(1+i)^n-2+…+P(1+i)+P

Якщо цю суму записати в оберненому порядку, то одержимо суму геометричної прогресії п членів, з першим членом b₂ = Р та знаменником q = 1 + і. Тому, згідно з формулою суми скінченної геометричної прогресії маємо

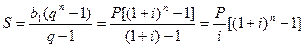(3)

Зауваження. 1) Якщо у формулі (3) покласти Р= 100, i=0,005, то ми одержимо результат прикладу 1.

2) У фінансових розрахунках формула (3) використовується у ви­гляді

S=P*s_n/i (4)

де значення s_n/i для різних n та і вказані в спеціальних розрахункових таблицях (дивись, наприклад, таблицю 1).

Так, розв'язок прикладу 1. а) за формулою (4) буде згідно таблично­му значенню s_n/i:

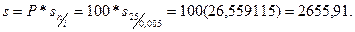
2. Розрахунки ренти

Деяка частина населення держав з ринковою економікою живе за рахунок ренти, тобто регулярно на протязі певного терміну (наприклад, спочатку кожного року на протязі 20 років) одер­жують раніше обумовлену величину коштів з відповідного ра­хунка в банку або страховій компанії.

Виникає задача: скільки коштів треба покласти на рахунок ренти для виконання відповідних умов?

Перш ніж розв'язати цю задачу у загальному випадку, розгля­немо конкретний приклад.

Приклад 2. В день 60-річчя містер Стоун відкрив рахунок ренти в страховій компанії на своє ім'я з умовами, що він буде одержувати щорічно у свій день народження, починаю­чи з наступного року 5000 доларів на протязі 10 років. Ком­панія прийняла його кошти і відкрила йому рахунок ренти з щорічним зростанням вкладених коштів на 8%. Яку суму вне­сено на рахунок ренти містера Стоуна?

Розв'язування. Позначимо через А₁ частину усього внеску, яка за­безпечила виконання умов містера Стоуна та компанії через 1 рік, тобто у день 61-річчя. Ця частина ренти на протязі одного року знаходи­лась на рахунку і тому, згідно з умовою страхової компанії, одержала 8% прибутку, тобто стала 1,08А₁ За умовою містера Стоуна ця величи­на повинна дорівнювати 5000 доларів. Отже, з рівності

1,08А₁=5000 знаходимо

А₁=5000(1,08)^-1

Таким чином, саме таку суму коштів треба було внести на рахунок у день 60-річчя для того, щоб у день 61 річниці одержати 5 000 доларів.

Тепер позначимо через А₂ частину первинного внеску, яка через два роки буде сплаченою у кількості 5 000 доларів. Ця частина ренти зна­ходилась на рахунку на протязі двох років і одержала щорічно 8% при­бутку, тобто прийняла значення (1,08)²А₂. З рівності (1,08)²А₂=5000 випливає

А₂ = 5000(1,08)^-2.

Таким чином, якщо вклад на рахунок ренти дорівнював А₂, то в день 62 річниці містер Стоун одержав 5000 доларів. Якщо містер Сто­ун у день свого 60-річчя зробив внесок на рахунок ренти величиною А₁+А₂, тоді його умова одержання 5 000 доларів у дні 61 та 62 річниць буде задоволена.

Аналогічно можна впевнитись, що внесок

А₃ = 5000(1,08)^-3

дозволить йому отримати 5 000 доларів у день 63 річниці і т.д. Для одержання останніх 5000 доларів у день 70-річчя треба було зробити початковий внесок величиною

А₁₀ = 5000(1,08)^-10.

Для повного виконання умов містера Стоуна, він повинен одержу­вати 5 000 доларів усі 10 років, а тому загальний внесок на рахунок ренти повинен бути

А = А₁ + А₂ + А₃ + ... + А₁₀ = 5000(1,08)^-1 + 5000(1,08)^-2 + + 5000(1,08)^-3+ ... + 5000(1,08)^-10

Таким чином, шукана величина внеску А на рахунок ренти є сума 10 членів геометричної прогресії з першим членом b₁=5000(1,08)^-1 і знаменником q=(1,08)^-1, її сумою буде

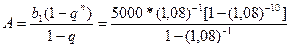
Помножимо чисельник та знаменник дробу на (1,08) тоді одержимо

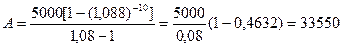
Отже, містер Стоун повинен вкласти на рахунок ренти 33 550 до­ларів, щоб одержувати по 5 000 доларів щорічно на протязі 10 років.

Тепер розглянемо загальний випадок ренти.

Позначимо через А величину внеску на рентний рахунок. Нехай з цього рахунку роблять виплати розміром Р регулярно, з постійним періодом часу на протязі n періодів, починаючи через один після відкриття рахунка ренти. Нехай величина внеску зростає кожного періода на R відсотків.

Як і в прикладі 2, щоб отримати першу виплату у розмірі Р після першого періода часу треба вкласти в рахунок ренти таку кількість коштів А₁, яка задовольняє рівність

A₁(1+i)=P,

де 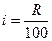. З цієї рівності знаходимо значення А₁ вигляду

А₁=Р(1+і)^-1

Аналогічно знаходимо внесок А₂, який зростає до Р після двох періодів часу

А₂=Р(1+і)^-2

а також частину внеску А_n, яка зростає до Р після n періодів

А_n=Р(1+і)^-n

Загальна величина внеску А на рахунок ренти є сумою

А=А1+А2+…+Аn=Р(1+і)^-1+Р(1+і)^-2+…+Р(1+і)^-n

Тобто А – це сума геометричної прогресії n членів, перший Фінансисти використовують

формулу (5) у вигляді

(б),

де а_п/ =/ '[1-(1+Л "] табульована для різних значень і = -г=гт

Л 100

та п.

Наприклад, а_|0/ =6,710081 у таблиці, тому

/0.08

А = Ра_10/ = 5000а_І0/ =5000-6,710081 = 33550,

/0,08 /0,08

як і в прикладі 2.де і = -т~ . З цієї рівності знаходимо значення А, вигляду

Аналогічно знаходимо внесок А^, який зростає до Р після двох періодів часу

А₂ = Р(1-м)-²,

а також частину внеску А,,, яка зростає до Р після п періодів

ш* Приклад 3. Щорічна рента.

Місіс Стоун у свою 59 річницю зробила внесок 120000 до­ларів у страхову компанію, як ренту. Компанія страхування життя погодилась надавати місіс Стоун 6% щорічного прибутку з внеску і проводити щорічні виплати на протязі 15 років. Скіль­ки коштів щорічно буде одержувати місіс Стоун з цього рахунку?

Розв 'язання. У даному випадку відома величина внеску на рахунок ренти А= 120000, а також відсоток прибутку К=6, тобто

Загальна величина внеску А на рахунок ренти є сумою

Підставимо значення А та і у формулу (5) або (6) в одержимо шука­ну величину Р:тобто А — це сума геометричної прогресії п членів, перший член якої Ь₁ = Р(1 + /)"¹, а знаменник ч = (1 + і) '■ Тому

120000= Р-а_15/ =Р-9,712249

ЛІ,06

(значення а взято з таблиці 1).

Питання для самоконтролю

1. Рахунки накопичення

2. Розрахунки ренти

3. Погашення боргу