Теорема 1. Загальний член арифметичної прогресії може бути знайдений за формулою

Дата: 2025-06-14; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

a_n = a ₁ +( n -1) d (1)

Доведення проведемо методом математичної індукції. Згідно з формулою (1) маємо a ₂ = a ₂+2d

a ₃ = a ₂ + d = a ₁ +2 d

Нехай має місце (1) для деякого n і доведемо її для n +1.

Згідно з означенням: a_{n +1} = a_n + d .

Підставивши у цю рівність замість a_n його значення з (1), одержимо:

a_n+1=a₁+(n-1)d+d = a₁+nd або a_n+1=a₁+[(n + 1)-1]d

Остання рівність – це формула (1) записана для n +1, яку й треба було довести.

2. Властивості арифметичної прогресії

Кожен член арифметичної прогресії a ₁, a ₂, a ₃,…, a_n, починаючи з другого, дорівнює середньому арифметичному двох сусідніх з ним членів, тобто

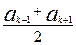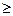a_k = , k 2 (2)

Дійсно, якщо a_k = a_{k -1} + d , a_{k +1} = a_k + d 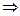a_k = a_{k -1} – d .

Сума цих рівностей дає: 2 a_k = a_{k -1} + a_{k +1} звідки випливає формула (2).

Сума двох членів скінченої арифметичної прогресії, рівновіддалених від її кінців, дорівнює сумі крайніх членів цієї прогресії, тобто

a_k + a_n-k+1 =a₁ + a_n , k 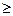2 (3)

Дійсно, a_k + a_n-k+1 =[ a₁+(k-1)d]+[ a₁+(n-k)d]=2a₁+(n-1)d;

a₁ + a_n=a₁+ a₁+ (n-1)d=2a₁+(n-1)d.

Праві частини цих рівностей співпадають, тому їх ліві частини рівні, тобто має місце рівняння (3) для k 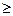2.

Сума членів скінченої арифметично прогресії дорівнює добутку півсуми крайніх її членів на число всіх членів:

S_n = 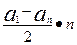(4)

Для доведення цього твердження запишемо суму S_n арифметичної прогресії двома способами:

S_n = a₁ + a ₂ + …+ a_{n -1} + a_n

S_n = a_{n -1} + а _n + …+ a ₂ + a₁

Додавши почленно ліву і праву частини, одержимо згідно формули (3):

2 S_n = ( a ₁ + a_n )* n ,

Звідки і випливає формула (4)

Наслідок. Якщо замість a_n підставити у формулу (4) його значення у вигляді (1) , тоді одержимо другу формулу для суми членів арифметичної прогресії:

S_n = 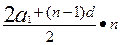(5)

3. Поняття простих відсотків на капітал

Якщо сума коштів Р вкладена під R відсотків річних, то після першого року буде одержано прибуток величиною d= .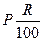

Якщо вкладення капіталу здійснюється під простий річний відсоток, тоді з кожним роком прибуток зростає на однакову величину. Тому послідовність значень капіталу буде Р, P + d , P +2 d , P +3 d ,… тобто ці значення утворюють арифметичну прогресію.

Отже, величина капіталу Р, вкладеного під простий річний відсоток R , через n років буде a_n = P + n * d = P + n * 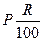= P(1+ ).

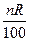Наприклад, якщо вкладено 5000 гривень під простий річний відсоток 10%, тоді через 5 років вкладник матиме:

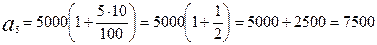гривень.

4. Геометрична прогресія та складні відсотки

Означення. Геометричною прогресією називається послідовність, кожний наступний член якої дорівнює попередньому, помноженому на одне і те ж саме число q , яке називають знаменником прогресії. Геометричну прогресію позначають .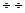

Згідно з означенням

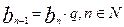(1)

Наприклад, 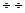1,3,9,27,…- геометрична прогресія із знаменником q =3.

Геометрична прогресія називається зростаючою, якщо 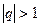і спадною, якщо .

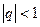Якщо кількість членів геометричної прогресії скінченна, то вона називається скінченною, у протилежному випадку вона називається нескінченою геометричною прогресією.

Методом математичної індукції можна довести, що загальний член геометричної прогресії знаходиться за формулою

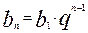(2)

5. Властивості геометричної прогресії

Будь-який член геометричної прогресії з додатним членом, починаючи з другого, дорівнює середньому геометричному двох сусідніх з ним членів:

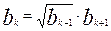(3)

Дійсно, за формулою (2) маємо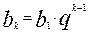

.

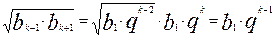
Бачимо, що обидві частини рівності (3) однакові.

Добутки членів скінченої геометричної прогресії, рівновіддалених від її кінців, рівні між собою, тобто

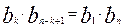(4)

Дійсно, ;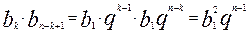

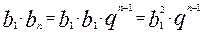
Отже, обидві частини рівності (4) однакові.

Сума членів скінченої геометричної прогресії може бути знайдена за формулою:

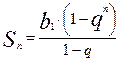(5)

Для доведення цієї формули знайдемо

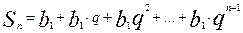(6)

Помноживши обидві частини цієї рівності на q , одержимо

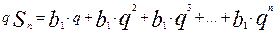(7)

Віднімемо почленно з рівності (6) рівність (7), тоді одержимо

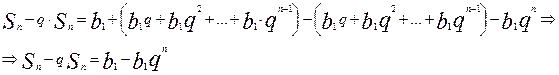
Тобто 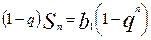. З останньої рівності випливає формула (5).

Суму всіх членів спадної нескінченої прогресії знаходять за формулою

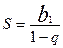(8)

Доведення. Члени геометричної прогресії спадають, тому .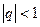

Розглянемо суму членів вказаної геометричної прогресії як границю скінченої геометричної прогресії. Тоді

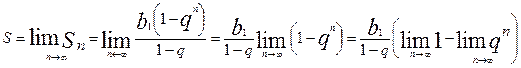
Але 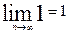, 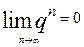. Отже, 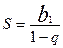, що і треба було довести.

6. Поняття складних відсотків на капітал

Припустимо, що вкладник надає банку 5000 гривень з умовою їх зростання кожного року на 10 складних відсотків. Це означає: кожного року величина капіталу, що знаходиться на рахунку вкладника у банку, повинна зростати на 10 відсотків.

Після першого року величина вкладення буде

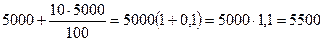гривень

Після другого року величина вкладення буде

,

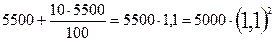А після n років величина вкладення буде .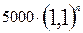

Отже, величина капіталу з роками змінюється таким чином:

,

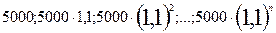Тобто вона утворює геометричну прогресію із знаменником q =1,1 та першим членом b₁ = 5000.

Тому величина капіталу Р, що зростає кожного року на R складних відсотків, через n років приймає значення

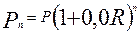(9)

У розглянутому вище випадку вкладник через 5 років буде володіти капіталом, який дорівнює:

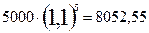(гривень),

А через 10 років капітал становитиме

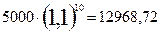(гривень)

(у випадку простого відсотка, згідно з прикладом розділу 3.2 величина вкладу через 5 років буде 7500 гривень)

Питання для самоконтролю

1. Арифметична прогресія та прості відсотки

2. Властивості арифметичної прогресії